
題目列表(包括答案和解析)
(本小題滿分12分)
已知函數(shù)![]()
(1)確定![]() 上的單調(diào)性;[來源:學(xué)科網(wǎng)]
上的單調(diào)性;[來源:學(xué)科網(wǎng)]
(2)設(shè)![]() 在(0,2)上有極值,求
在(0,2)上有極值,求![]() 的取值范圍。
的取值范圍。
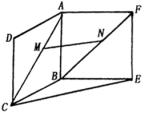
(本小題滿分12分)如圖,ABCD和ABEF都是正方形,![]() ,且
,且![]() .證明:
.證明:![]() 平面BCE.
平面BCE.
[來源:學(xué)&科&網(wǎng)]
(本小題滿分12分)[來源:學(xué)科網(wǎng)ZXXK]
某校高三文科分為四個班.高三數(shù)學(xué)調(diào)研測試后,
隨機(jī)地在各班抽取部分學(xué)生進(jìn)行測試成績統(tǒng)計(jì),
各班被抽取的學(xué)生人數(shù)恰好成等差數(shù)列,人數(shù)最少的班被抽取了22人。
抽取出來的所有學(xué)生的測試成績統(tǒng)計(jì)結(jié)果的頻率分布條形圖如圖5所示,
其中120~130(包括120分但不包括130分)的頻率為0.05,此 0
分?jǐn)?shù)段的人數(shù)為5人![]()

(1)問各班被抽取的學(xué)生人數(shù)各為多少人?
(2)在抽取的所有學(xué)生中,任取一名學(xué)生, 求分?jǐn)?shù)不小(![]() 本小題滿分12分)
本小題滿分12分)
(本小題滿分12分)
如圖所示,在正三棱柱![]() 中,底面邊長為
中,底面邊長為![]() ,側(cè)棱長為
,側(cè)棱長為![]() ,
,![]() 是棱
是棱![]() 的中點(diǎn).
的中點(diǎn).
| |
(Ⅱ)求二面角![]() 的大小;[來源:學(xué)科網(wǎng)ZXXK]
的大小;[來源:學(xué)科網(wǎng)ZXXK]
(Ⅲ)求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
(本小題滿分12分)
班主任為了對本班學(xué)生的考試成績進(jìn)行分析,決定從全班25位女同學(xué),15位男同學(xué)中隨機(jī)抽取一個容量為8的樣本進(jìn)行分析.
(1)如果按性別比例分層抽樣,可以得到多少個不同的樣本(只要求寫出算式即可,不必計(jì)算出結(jié)果);
(2)隨機(jī)抽取8位同學(xué),數(shù)學(xué)分![]() 數(shù)依次為:60,65,70,75,80,85,90,95;
數(shù)依次為:60,65,70,75,80,85,90,95;
物理成績依次為:72,77,80,84,88,90,93,95,
①若規(guī)定90分(含90分)以上為優(yōu)秀,記![]() 為這8位同學(xué)中數(shù)學(xué)和物理分?jǐn)?shù)均為優(yōu)秀的人數(shù),求
為這8位同學(xué)中數(shù)學(xué)和物理分?jǐn)?shù)均為優(yōu)秀的人數(shù),求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
②若這8位同學(xué)的數(shù)學(xué)、物理分?jǐn)?shù)事實(shí)上對應(yīng)下表:
| 學(xué)生編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7[來源:Z#xx#k.Com] | 8 |
| 數(shù)學(xué)分?jǐn)?shù) | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分?jǐn)?shù) | 72 | 77 | 80[來源:學(xué)科網(wǎng)] | 84 | 88 | 90 | 93 | 95 |
根據(jù)上表數(shù)據(jù)可知,變量![]() 與
與![]() 之間具有較強(qiáng)的線性相關(guān)關(guān)系,求出
之間具有較強(qiáng)的線性相關(guān)關(guān)系,求出![]() 與
與![]() 的線性回歸方程(系數(shù)精確到0.01).(參考公式:
的線性回歸方程(系數(shù)精確到0.01).(參考公式:![]() ,其中
,其中 ,
,![]() ;參考數(shù)據(jù):
;參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
一、選擇題:1-5 :A D B D C 6-10: C C C
D B 11-12: B B2009屆高三第六次月考數(shù)學(xué)理科試題.files/image007.jpg) 學(xué)科網(wǎng)
學(xué)科網(wǎng)
二、填空題: 13, 2009屆高三第六次月考數(shù)學(xué)理科試題.files/image300.gif) 14. 3 15.
14. 3 15.2009屆高三第六次月考數(shù)學(xué)理科試題.files/image302.gif) 16. (1,2),(3,402)
16. (1,2),(3,402)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image007.jpg) 學(xué)科網(wǎng)
學(xué)科網(wǎng)
三、解答題
三、解答題(本大題共6小題,共70分)
17.(12分)
解:(1)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image304.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image222.gif) ∥
∥2009屆高三第六次月考數(shù)學(xué)理科試題.files/image226.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image306.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image308.gif) 2分
2分
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image310.gif) 4分
4分
又2009屆高三第六次月考數(shù)學(xué)理科試題.files/image312.gif) 為銳角
為銳角 2009屆高三第六次月考數(shù)學(xué)理科試題.files/image314.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image316.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image318.gif) 6分
6分
(Ⅱ)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image304.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image321.gif) 由
由 2009屆高三第六次月考數(shù)學(xué)理科試題.files/image323.gif) 得
得 2009屆高三第六次月考數(shù)學(xué)理科試題.files/image325.gif)
又2009屆高三第六次月考數(shù)學(xué)理科試題.files/image327.gif) 代入上式得:
代入上式得:2009屆高三第六次月考數(shù)學(xué)理科試題.files/image329.gif) (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image331.gif) 時等號成立。) 9分
時等號成立。) 9分
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image232.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image333.gif) (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image331.gif) 時等號成立。) 11分
時等號成立。) 11分
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image306.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image212.gif) 的面積
的面積2009屆高三第六次月考數(shù)學(xué)理科試題.files/image232.gif) 的取值范圍為.
的取值范圍為.2009屆高三第六次月考數(shù)學(xué)理科試題.files/image336.gif) 12分
12分
18.(12分)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image338.gif) 解法一:
解法一:
(Ⅰ)取2009屆高三第六次月考數(shù)學(xué)理科試題.files/image094.gif) 中點(diǎn)
中點(diǎn)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image341.gif) ,連結(jié)
,連結(jié)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image343.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image345.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image347.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image349.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image351.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image353.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image355.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image357.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image359.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image357.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image362.gif) .
.
(Ⅱ)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image349.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image365.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image367.gif) .
.
又2009屆高三第六次月考數(shù)學(xué)理科試題.files/image242.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image370.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image372.gif) 又
又2009屆高三第六次月考數(shù)學(xué)理科試題.files/image238.gif) ,即
,即2009屆高三第六次月考數(shù)學(xué)理科試題.files/image375.gif) ,且
,且2009屆高三第六次月考數(shù)學(xué)理科試題.files/image377.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image379.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image381.gif) .
.
取2009屆高三第六次月考數(shù)學(xué)理科試題.files/image383.gif) 中點(diǎn)
中點(diǎn)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image385.gif) .連結(jié)
.連結(jié)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image387.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image389.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image391.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image393.gif) 是
是2009屆高三第六次月考數(shù)學(xué)理科試題.files/image395.gif) 在平面
在平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image381.gif) 內(nèi)的射影,
內(nèi)的射影,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image398.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image400.gif) 是二面角
是二面角2009屆高三第六次月考數(shù)學(xué)理科試題.files/image246.gif) 的平面角.
的平面角.
在2009屆高三第六次月考數(shù)學(xué)理科試題.files/image403.gif) 中,
中,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image405.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image407.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image409.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image411.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image413.gif) .
.2009屆高三第六次月考數(shù)學(xué)理科試題.files/image306.gif) 二面角
二面角2009屆高三第六次月考數(shù)學(xué)理科試題.files/image246.gif) 的余弦值為
的余弦值為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image417.gif)
(Ⅲ)由(Ⅰ)知2009屆高三第六次月考數(shù)學(xué)理科試題.files/image419.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image357.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image306.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image423.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image357.gif) .
.
過2009屆高三第六次月考數(shù)學(xué)理科試題.files/image132.gif) 作
作2009屆高三第六次月考數(shù)學(xué)理科試題.files/image427.gif) ,垂足為
,垂足為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image429.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image304.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image432.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image434.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image436.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image249.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image439.gif) 的長即為點(diǎn)
的長即為點(diǎn)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image132.gif) 到平面
到平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image249.gif) 的距離.
的距離.
由(Ⅰ)知2009屆高三第六次月考數(shù)學(xué)理科試題.files/image244.gif) ,又
,又2009屆高三第六次月考數(shù)學(xué)理科試題.files/image242.gif) ,且
,且2009屆高三第六次月考數(shù)學(xué)理科試題.files/image445.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image447.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image449.gif) .
.2009屆高三第六次月考數(shù)學(xué)理科試題.files/image451.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image449.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image454.gif) .
.
在2009屆高三第六次月考數(shù)學(xué)理科試題.files/image456.gif) 中,
中,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image458.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image460.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image462.gif) .
.2009屆高三第六次月考數(shù)學(xué)理科試題.files/image464.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image306.gif) 點(diǎn)
點(diǎn)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image132.gif) 到平面
到平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image249.gif) 的距離為
的距離為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image469.gif) .
.
解法二:
(Ⅰ)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image349.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image365.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image367.gif) .
.
又2009屆高三第六次月考數(shù)學(xué)理科試題.files/image242.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image370.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image476.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image447.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image449.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image480.gif) 平面
平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image449.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image362.gif) .
.
(Ⅱ)如圖,以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image132.gif) 為原點(diǎn)建立空間直角坐標(biāo)系
為原點(diǎn)建立空間直角坐標(biāo)系2009屆高三第六次月考數(shù)學(xué)理科試題.files/image485.gif) .
.
則2009屆高三第六次月考數(shù)學(xué)理科試題.files/image487.gif) .設(shè)
.設(shè)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image489.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image491.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image493.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image495.gif) .
.
取2009屆高三第六次月考數(shù)學(xué)理科試題.files/image383.gif) 中點(diǎn)
中點(diǎn)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image385.gif) ,連結(jié)
,連結(jié)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image387.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image500.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image502.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image398.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image505.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image400.gif) 是二面角
是二面角2009屆高三第六次月考數(shù)學(xué)理科試題.files/image246.gif) 的平面角.
的平面角.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image509.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image511.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image513.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image515.gif) .
.2009屆高三第六次月考數(shù)學(xué)理科試題.files/image306.gif) 二面角
二面角2009屆高三第六次月考數(shù)學(xué)理科試題.files/image246.gif) 的余弦值為
的余弦值為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image417.gif) .
.
(Ⅲ)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image520.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image522.gif) 在平面
在平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image249.gif) 內(nèi)的射影為正
內(nèi)的射影為正2009屆高三第六次月考數(shù)學(xué)理科試題.files/image525.gif) 的中心
的中心2009屆高三第六次月考數(shù)學(xué)理科試題.files/image429.gif) ,且
,且2009屆高三第六次月考數(shù)學(xué)理科試題.files/image528.gif) 的長為點(diǎn)
的長為點(diǎn)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image132.gif) 到平面
到平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image249.gif) 的距離.
的距離.
如(Ⅱ)建立空間直角坐標(biāo)系2009屆高三第六次月考數(shù)學(xué)理科試題.files/image485.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image533.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image306.gif) 點(diǎn)
點(diǎn)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image429.gif) 的坐標(biāo)為
的坐標(biāo)為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image537.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image539.gif) .
.2009屆高三第六次月考數(shù)學(xué)理科試題.files/image306.gif) 點(diǎn)
點(diǎn)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image132.gif) 到平面
到平面2009屆高三第六次月考數(shù)學(xué)理科試題.files/image249.gif) 的距離為
的距離為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image469.gif) .
.
19.(12分)
解:(Ⅰ)由條件得2009屆高三第六次月考數(shù)學(xué)理科試題.files/image545.gif) ,又
,又2009屆高三第六次月考數(shù)學(xué)理科試題.files/image547.gif) 時,
時,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image549.gif) ,
,
故數(shù)列2009屆高三第六次月考數(shù)學(xué)理科試題.files/image551.gif) 構(gòu)成首項(xiàng)為1,公式為
構(gòu)成首項(xiàng)為1,公式為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image553.gif) 的等比數(shù)列.從而
的等比數(shù)列.從而2009屆高三第六次月考數(shù)學(xué)理科試題.files/image555.gif) ,即
,即2009屆高三第六次月考數(shù)學(xué)理科試題.files/image557.gif) .
.
(Ⅱ)由2009屆高三第六次月考數(shù)學(xué)理科試題.files/image559.gif) 得
得2009屆高三第六次月考數(shù)學(xué)理科試題.files/image561.gif) ,
,
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image563.gif) ,
,
兩式相減得 : 2009屆高三第六次月考數(shù)學(xué)理科試題.files/image565.gif) ,
所以
,
所以 2009屆高三第六次月考數(shù)學(xué)理科試題.files/image567.gif) .
.
(Ⅲ)由2009屆高三第六次月考數(shù)學(xué)理科試題.files/image569.gif) 得
得
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image571.gif)
所以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image573.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image575.gif) .
.
20.(12分)
解:(Ⅰ)①當(dāng)0<t2009屆高三第六次月考數(shù)學(xué)理科試題.files/image577.gif) 10時,V(t)=(-t2+14t-40)
10時,V(t)=(-t2+14t-40)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image579.gif)
化簡得t2-14t+40>0,
解得t<4,或t>10,又0<t2009屆高三第六次月考數(shù)學(xué)理科試題.files/image577.gif) 10,故0<t<4.
10,故0<t<4.
②當(dāng)10<t2009屆高三第六次月考數(shù)學(xué)理科試題.files/image577.gif) 12時,V(t)=4(t-10)(3t-41)+50<50,
12時,V(t)=4(t-10)(3t-41)+50<50,
化簡得(t-10)(3t-41)<0,
解得10<t<2009屆高三第六次月考數(shù)學(xué)理科試題.files/image581.gif) ,又10<t
,又10<t2009屆高三第六次月考數(shù)學(xué)理科試題.files/image577.gif) 12,故 10<t
12,故 10<t2009屆高三第六次月考數(shù)學(xué)理科試題.files/image577.gif) 12.
12.
綜合得0<t<4,或10<t2009屆高三第六次月考數(shù)學(xué)理科試題.files/image577.gif) 12,
12,
故知枯水期為1月,2月, 3月,4月,11月,12月共6個月.
(Ⅱ)由(Ⅰ)知:V(t)的最大值只能在(4,10)內(nèi)達(dá)到.
由V′(t)=2009屆高三第六次月考數(shù)學(xué)理科試題.files/image583.gif)
令V′(t)=0,解得t=8(t=-2舍去).
當(dāng)t變化時,V′(t) 與V (t)的變化情況如下表:
t
(4,8)
8
(8,10)
V′(t)
+
0
-
V(t)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image584.gif)
極大值
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image585.gif)
由上表,V(t)在t=8時取得最大值V(8)=8e2+50-108.32(億立方米).
故知一年內(nèi)該水庫的最大蓄水量是108.32億立方米
21.(12分)
解:(Ⅰ)由題意得直線2009屆高三第六次月考數(shù)學(xué)理科試題.files/image274.gif) 的方程為
的方程為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image588.gif) .
.
因?yàn)樗倪呅?sub>2009屆高三第六次月考數(shù)學(xué)理科試題.files/image268.gif) 為菱形,所以
為菱形,所以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image591.gif) .
.
于是可設(shè)直線2009屆高三第六次月考數(shù)學(xué)理科試題.files/image279.gif) 的方程為
的方程為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image594.gif) .
.
由2009屆高三第六次月考數(shù)學(xué)理科試題.files/image596.gif) 得
得2009屆高三第六次月考數(shù)學(xué)理科試題.files/image598.gif) .
.
因?yàn)?sub>2009屆高三第六次月考數(shù)學(xué)理科試題.files/image270.gif) 在橢圓上,
在橢圓上,
所以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image601.gif) ,解得
,解得2009屆高三第六次月考數(shù)學(xué)理科試題.files/image603.gif) .
.
設(shè)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image270.gif) 兩點(diǎn)坐標(biāo)分別為
兩點(diǎn)坐標(biāo)分別為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image606.gif) ,
,
則2009屆高三第六次月考數(shù)學(xué)理科試題.files/image608.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image610.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image612.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image614.gif) .
.
所以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image616.gif) .
.
所以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image279.gif) 的中點(diǎn)坐標(biāo)為
的中點(diǎn)坐標(biāo)為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image619.gif) .
.
由四邊形2009屆高三第六次月考數(shù)學(xué)理科試題.files/image268.gif) 為菱形可知,點(diǎn)
為菱形可知,點(diǎn)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image619.gif) 在直線
在直線2009屆高三第六次月考數(shù)學(xué)理科試題.files/image588.gif) 上,
上,
所以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image623.gif) ,解得
,解得2009屆高三第六次月考數(shù)學(xué)理科試題.files/image625.gif) .
.
所以直線2009屆高三第六次月考數(shù)學(xué)理科試題.files/image279.gif) 的方程為
的方程為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image628.gif) ,即
,即2009屆高三第六次月考數(shù)學(xué)理科試題.files/image630.gif) .
.
(Ⅱ)因?yàn)樗倪呅?sub>2009屆高三第六次月考數(shù)學(xué)理科試題.files/image268.gif) 為菱形,且
為菱形,且2009屆高三第六次月考數(shù)學(xué)理科試題.files/image281.gif) ,
,
所以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image634.gif) .
.
所以菱形2009屆高三第六次月考數(shù)學(xué)理科試題.files/image268.gif) 的面積
的面積2009屆高三第六次月考數(shù)學(xué)理科試題.files/image637.gif) .
.
由(Ⅰ)可得2009屆高三第六次月考數(shù)學(xué)理科試題.files/image639.gif) ,
,
所以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image641.gif) .
.
所以當(dāng)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image643.gif) 時,菱形
時,菱形2009屆高三第六次月考數(shù)學(xué)理科試題.files/image268.gif) 的面積取得最大值
的面積取得最大值2009屆高三第六次月考數(shù)學(xué)理科試題.files/image646.gif) .
.
22.(10分)解:從⊙O外一點(diǎn)P向圓引兩條切線PA、PB和割線PCD。從A點(diǎn)作弦AE平行于CD,連結(jié)BE交CD于F。求證:BE平分CD.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image648.gif) 【分析1】構(gòu)造兩個全等△.
【分析1】構(gòu)造兩個全等△.
連結(jié)ED、AC、AF。
CF=DF←△ACF≌△EDF←
←2009屆高三第六次月考數(shù)學(xué)理科試題.files/image649.gif)
←∠PAB=∠AEB=∠PFB
【分析2】利用圓中的等量關(guān)系。連結(jié)OF、OP、OB.2009屆高三第六次月考數(shù)學(xué)理科試題.files/image651.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image652.gif)
←∠PFB=∠POB←
←2009屆高三第六次月考數(shù)學(xué)理科試題.files/image653.gif)
23.(10分)解:(Ⅰ)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image655.gif) 是圓,
是圓,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image657.gif) 是直線.
是直線.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image655.gif) 的普通方程為
的普通方程為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image660.gif) ,圓心
,圓心2009屆高三第六次月考數(shù)學(xué)理科試題.files/image662.gif) ,半徑
,半徑2009屆高三第六次月考數(shù)學(xué)理科試題.files/image664.gif) .
.
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image657.gif) 的普通方程為
的普通方程為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image667.gif) .
.
因?yàn)閳A心2009屆高三第六次月考數(shù)學(xué)理科試題.files/image655.gif) 到直線
到直線2009屆高三第六次月考數(shù)學(xué)理科試題.files/image667.gif) 的距離為
的距離為2009屆高三第六次月考數(shù)學(xué)理科試題.files/image671.gif) ,所以
,所以2009屆高三第六次月考數(shù)學(xué)理科試題.files/image657.gif) 與
與2009屆高三第六次月考數(shù)學(xué)理科試題.files/image655.gif) 只有一個公共點(diǎn).
只有一個公共點(diǎn).
(Ⅱ)壓縮后的參數(shù)方程分別為
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image675.gif) :
:2009屆高三第六次月考數(shù)學(xué)理科試題.files/image677.gif) (
(2009屆高三第六次月考數(shù)學(xué)理科試題.files/image160.gif) 為參數(shù));
為參數(shù)); 2009屆高三第六次月考數(shù)學(xué)理科試題.files/image680.gif) :
:2009屆高三第六次月考數(shù)學(xué)理科試題.files/image682.gif) (t為參數(shù)).
(t為參數(shù)).
化為普通方程為:2009屆高三第六次月考數(shù)學(xué)理科試題.files/image675.gif) :
:2009屆高三第六次月考數(shù)學(xué)理科試題.files/image684.gif) ,
,2009屆高三第六次月考數(shù)學(xué)理科試題.files/image680.gif) :
:2009屆高三第六次月考數(shù)學(xué)理科試題.files/image686.gif) ,
,
聯(lián)立消元得2009屆高三第六次月考數(shù)學(xué)理科試題.files/image688.gif) ,其判別式
,其判別式2009屆高三第六次月考數(shù)學(xué)理科試題.files/image690.gif) ,
,
所以壓縮后的直線2009屆高三第六次月考數(shù)學(xué)理科試題.files/image680.gif) 與橢圓
與橢圓2009屆高三第六次月考數(shù)學(xué)理科試題.files/image675.gif) 仍然只有一個公共點(diǎn),和
仍然只有一個公共點(diǎn),和2009屆高三第六次月考數(shù)學(xué)理科試題.files/image655.gif) 與
與2009屆高三第六次月考數(shù)學(xué)理科試題.files/image657.gif) 公共點(diǎn)個數(shù)相同.
公共點(diǎn)個數(shù)相同.
24.(10分)解:
(Ⅰ)2009屆高三第六次月考數(shù)學(xué)理科試題.files/image694.gif)
圖像如下:
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image695.gif)
2009屆高三第六次月考數(shù)學(xué)理科試題.files/image696.gif)
(Ⅱ)不等式
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com