
題目列表(包括答案和解析)
| 2 |
| 2 |
| AM |
| MB |
| 1 |
| 2 |
已知雙曲線的中心在原點,以兩條坐標軸為對稱軸,離心率是![]() ,兩準線間的距離大于
,兩準線間的距離大于![]() ,且雙曲線上動點P到A(2,0)的最近距離為1。
,且雙曲線上動點P到A(2,0)的最近距離為1。
(Ⅰ)求證:該雙曲線的焦點不在y軸上;
(Ⅱ)求雙曲線的方程;
(Ⅲ)如果斜率為k的直線L過點M(0,3),與該雙曲線交于A、B兩點,若![]() ,試用l表示k2,并求當
,試用l表示k2,并求當![]() 時,k的取值范圍。
時,k的取值范圍。
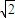 ,兩準線間的距離大于
,兩準線間的距離大于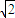 ,且雙曲線上動點P到A(2,0)的最近距離為1.
,且雙曲線上動點P到A(2,0)的最近距離為1.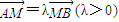 ,試用l表示k2,并求當
,試用l表示k2,并求當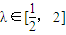 時,k的取值范圍.
時,k的取值范圍.| 1 |
| 2 |
| 3 |
| PS |
| QS |
 ,一條漸近線方程是
,一條漸近線方程是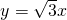 ,線段PQ是過曲線C右焦點F的一條弦,R是弦PQ的中點.
,線段PQ是過曲線C右焦點F的一條弦,R是弦PQ的中點. =0.當點P在曲線C上運動時,求a的取值范圍.
=0.當點P在曲線C上運動時,求a的取值范圍.
19.解:(1) 平面ABC,AB
平面ABC,AB 平面ABC,∵
平面ABC,∵ AB.
AB.
又 平面
平面 ,且AB
,且AB 平面
平面 ,∴
,∴ 又
又
∴ 平面
平面 .
.
(2) BC∥
BC∥ ,∴
,∴ 或其補角就是異面直線
或其補角就是異面直線 與BC所成的角.
與BC所成的角.
由(1)知 又AC=2,∴AB=BC=
又AC=2,∴AB=BC= ,∴
,∴ .
.
在 中,由余弦定理知cos
中,由余弦定理知cos
∴ =
= ,即異面直線
,即異面直線 與BC所成的角的大小為
與BC所成的角的大小為
 (3)過點D作
(3)過點D作 于E,連接CE,由三垂線定理知
于E,連接CE,由三垂線定理知 ,故
,故
 是二面角
是二面角 的平面角,
的平面角,
又 ,∴E為
,∴E為 的中點,∴
的中點,∴ ,又
,又 ,由
,由
得 ,在Rt
,在Rt CDE中,sin
CDE中,sin ,所以二面角
,所以二面角 正弦值的大小為
正弦值的大小為
20.解:(1)因 ,
, ,故可得直線方程為:
,故可得直線方程為:
(2) ,
, ,用數學歸納法可證.
,用數學歸納法可證.
(3) ,
, ,
, ,
,
所以
21.解:(1)∵
函數 是R上的奇函數 ∴
是R上的奇函數 ∴  即
即 ∴
∴  ,由
,由 的任意性知
的任意性知 ∵
函數
∵
函數 在
在 處有極值,又
處有極值,又
∴  是關于
是關于 的方程
的方程 的根,即
的根,即 ①
①
∵  ∴
∴  ②(4分)由①、②解
②(4分)由①、②解 得
得
(2)由(1)知 ,
,
列表如下:






1
(1,3)
3

+
0
-
0
+


增函數
極大值1
減函數
極小值
增函數
9
∴  在
在 上有最大值9,最小值
上有最大值9,最小值
∵ 任意的 都有
都有 ∴
∴
 ,即
,即
∴  的取值范圍是
的取值范圍是
22.(1)
(2)由 得
得
 ①
①
設C ,CD中點為M
,CD中點為M ,則有
,則有 ,
, ,
,
 ,又A(0,-1)且
,又A(0,-1)且 ,
, ,
,
即 ,
,
 (此時
(此時 ) ②
) ②
將②代入①得 ,即
,即 或
或 ,
,
綜上可得 或
或 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com