
題目列表(包括答案和解析)
已知 ,且
,且 .
.
(1)求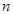 的值;
的值;
(2)求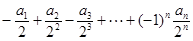 的值.
的值.
【解析】本試題主要考查了二項式定理的運用,以及系數求和的賦值思想的運用。第一問中,因為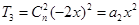 ,所以
,所以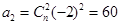 ,可得
,可得 ,第二問中,因為
,第二問中,因為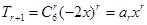 ,所以
,所以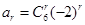 ,所以
,所以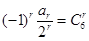 ,利用組合數性質可知。
,利用組合數性質可知。
解:(1)因為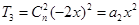 ,所以
,所以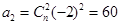 , ……3分
, ……3分
化簡可得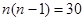 ,且
,且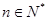 ,解得
,解得 . …………6分
. …………6分
(2)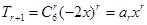 ,所以
,所以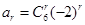 ,
,
所以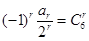 ,
,
| 氣溫(℃) | 18 | 13 | 10 | -1 |
| 用電量(度) | 24 | 34 | 38 | 64 |
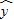 =bx+a中的b=-2,預測當氣溫為-10℃時,該單位用電量的度數約為 度.
=bx+a中的b=-2,預測當氣溫為-10℃時,該單位用電量的度數約為 度.已知過點 的動直線
的動直線 與拋物線
與拋物線 相交于
相交于 兩點.當直線
兩點.當直線 的斜率是
的斜率是 時,
時, .
.
(1)求拋物線 的方程;
的方程;
(2)設線段 的中垂線在
的中垂線在 軸上的截距為
軸上的截距為 ,求
,求 的取值范圍.
的取值范圍.
【解析】(1)B ,C
,C ,當直線
,當直線 的斜率是
的斜率是 時,
時,
 的方程為
的方程為 ,即
,即 (1’)
(1’)
聯立 得
得 ,
, (3’)
(3’)
由已知  ,
, (4’)
(4’)
由韋達定理可得 G方程為
G方程為 (5’)
(5’)
(2)設 :
: ,BC中點坐標為
,BC中點坐標為 (6’)
(6’)
 得
得 由
由 得
得 (8’)
(8’)


BC中垂線為 (10’)
(10’)

 (11’)
(11’)


| 氣溫(℃) | 18 | 13 | 10 | -1 |
| 用電量(度) | 24 | 34 | 38 | 64 |
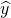 =bx+a中的b=-2,預測當氣溫為-10℃時,該單位用電量的度數約為________度.
=bx+a中的b=-2,預測當氣溫為-10℃時,該單位用電量的度數約為________度.已知函數 .
.
(Ⅰ)求函數 的單調區間;
的單調區間;
(Ⅱ)設 ,若對任意
,若對任意 ,
, ,不等式
,不等式 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
【解析】第一問利用 的定義域是
的定義域是

由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函數 的單調遞增區間是(1,3);單調遞減區間是
的單調遞增區間是(1,3);單調遞減區間是
第二問中,若對任意 不等式
不等式 恒成立,問題等價于
恒成立,問題等價于 只需研究最值即可。
只需研究最值即可。
解: (I) 的定義域是
的定義域是 ......1分
......1分
 ............. 2分
............. 2分
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函數 的單調遞增區間是(1,3);單調遞減區間是
的單調遞增區間是(1,3);單調遞減區間是 ........4分
........4分
(II)若對任意 不等式
不等式 恒成立,
恒成立,
問題等價于 ,
.........5分
,
.........5分
由(I)可知,在 上,x=1是函數極小值點,這個極小值是唯一的極值點,
上,x=1是函數極小值點,這個極小值是唯一的極值點,
故也是最小值點,所以 ; ............6分
; ............6分

當b<1時, ;
;
當 時,
時, ;
;
當b>2時, ;
............8分
;
............8分
問題等價于
 ........11分
........11分
解得b<1 或 或
或  即
即 ,所以實數b的取值范圍是
,所以實數b的取值范圍是
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com