
題目列表(包括答案和解析)
已知函數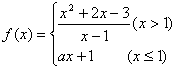 在點
在點![]() 處連續,則
處連續,則![]() 的值是( )
的值是( )
A.2 B.3 C.-2 D.-4
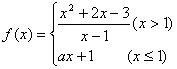 在點
在點A.2 B.3 C.-2 D.-4
設函數 在點
在點![]() 處連續,則實數
處連續,則實數![]() 的值是( )
的值是( )
A、2 B、1 C、0 D、-2
 在點
在點 處連續,則實數
處連續,則實數 的值是( )
的值是( )| A.2 | B.1 | C.0 | D.-2 |
已知函數 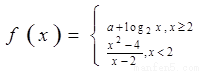 在點
在點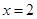 處連續,則常
處連續,則常
數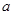 的值是
( )
的值是
( )
 2
2
 3
3
 4
4
 5
5
一、選擇題 1--5 DDCBA 6--10 ADBCA 11-12 AB
二、填空題 13. 14.12 15.
14.12 15. 16.AC
16.AC
三、解答題
17.解:(Ⅰ)  ,
,
 ,
,
 .
.
 ,
,
 ,
,  .
.
(Ⅱ)由余弦定理 ,得
,得  .
.
 ,
,  .
.
所以 的最小值為
的最小值為 ,當且僅當
,當且僅當 時取等號.
時取等號.
18、(Ⅰ)解法一:依據題意,因為隊伍從水路或陸路抵達災區的概率相等,則將“隊伍從水路或陸路抵達災區”視為同一個事件. 記“隊伍從水路或陸路抵達災區”為事件C,且B、C相互獨立,而且 .…………………………………… 2分
.…………………………………… 2分
在5月13日恰有1支隊伍抵達災區的概率是
 . ……………… 5分
. ……………… 5分
解法二:在5月13日恰有1支隊伍抵達災區的概率是

 .……………………………………………………………… 5分
.……………………………………………………………… 5分
(Ⅱ)依據題意,因為隊伍從水路或陸路抵達災區的概率相等,則將“隊伍從水路或陸路抵達災區”視為同一個事件. 記“隊伍從水路或陸路抵達災區”為事件C,且B、C相互獨立,而且 .
.
設5月13日抵達災區的隊伍數為 ,則
,則 =0、1、2、3、4. ……………… 6分
=0、1、2、3、4. ……………… 6分
由已知有: ;………………………………… 7分
;………………………………… 7分
 ;………………………… 8分
;………………………… 8分
 ;………………… 9分
;………………… 9分
 ;……………………… 10分
;……………………… 10分
 . ………………………………………………… 10分
. ………………………………………………… 10分
因此其概率分布為:

0
1
2
3
4
P





……………… 11分
所以在5月13日抵達災區的隊伍數 的數學期望為:
的數學期望為:
 =0×
=0× + 1×
+ 1× + 2×
+ 2× + 3×
+ 3× + 4×
+ 4× =
= .
.
答:在5月13日抵達災區的隊伍數 的數學期望
的數學期望 =
= . ………………
12分
. ………………
12分
19.(I)由已知a2-a1=-2, a3-a2=-1, -1-(-2)=1 ∴an+1-an=(a2-a1)+(n-1)?1=n-3
n≥2時,an=( an-an-1)+( an-1-an-2)+…+( a3-a2)+( a2-a1)+ a1
=(n-4)+(n-5) +…+(-1)+(-2)+6 =
n=1也合適. ∴an= (n∈N*) ……………………3分
(n∈N*) ……………………3分
又b1-2=4、b2-2=2 .而 ∴bn-2=(b1-2)?(
∴bn-2=(b1-2)?( )n-1即bn=2+8?(
)n-1即bn=2+8?( )n
)n
∴數列{an}、{bn}的通項公式為:an= ,bn=2+(
,bn=2+( )n-3…………… 6分
)n-3…………… 6分
(II)設
當k≥4時 為k的增函數,-8?(
為k的增函數,-8?( )k也為k的增函數,…………… 8分
)k也為k的增函數,…………… 8分
 而f(4)=
而f(4)=  ∴當k≥4時ak-bk≥
∴當k≥4時ak-bk≥ ………………10分
………………10分
又f(1)=f(2)=f(3)=0 ∴不存在k, 使f(k)∈(0, )…………12分
)…………12分
20、證(Ⅰ)因為 側面
側面 ,故
,故
在 中,
中, 由余弦定理有
由余弦定理有

 故有
故有

而  且
且 平面
平面

 ……………… 4分
……………… 4分
(Ⅱ)由
從而 且
且 故
故
不妨設  ,則
,則 ,則
,則
又 則
則
在 中有
中有
 從而
從而 (舍去)
(舍去)
故 為
為 的中點時,
的中點時, ……………… 8分
……………… 8分
法二:以 為原點
為原點 為
為 軸,設
軸,設 ,則
,則
 由
由 得
得 
即 
化簡整理得 
 或
或 
當 時
時 與
與 重合不滿足題意
重合不滿足題意
當 時
時 為
為 的中點
的中點
故 為
為 的中點使
的中點使 ……………… 8分
……………… 8分
(Ⅲ)取 的中點
的中點 ,
, 的中點
的中點 ,
, 的中點
的中點 ,
, 的中點
的中點
連 則
則 ,連
,連 則
則 ,連
,連 則
則
連 則
則 ,且
,且 為矩形,
為矩形,
又 故
故 為所求二面角的平面角……………… 10分
為所求二面角的平面角……………… 10分
 在
在 中,
中,

 ……………… 12分
……………… 12分
法二:由已知 ,
所以二面角
,
所以二面角 的平面角
的平面角 的大小為向量
的大小為向量 與
與 的夾角……………… 10分
的夾角……………… 10分
因為

故  ……………… 12分
……………… 12分
21.解:(I)由 ,
,
 ∴直線l的斜率為
∴直線l的斜率為 ,
,
故l的方程為 ,∴點A坐標為(1,0)……… 2分
,∴點A坐標為(1,0)……… 2分
設 則
則 ,
,
由 得
得

整理,得 ……………………4分
……………………4分
∴動點M的軌跡C為以原點為中心,焦點在x軸上,長軸長為 ,短軸長為2的橢圓 …… 5分
,短軸長為2的橢圓 …… 5分
(II)如圖,由題意知直線l的斜率存在且不為零,設l方程為y=k(x-2)(k≠0)①