
題目列表(包括答案和解析)
設函數(shù)![]() 的圖象關于直線
的圖象關于直線![]() 對稱.
對稱.
(1)求![]() 的值;
的值;
(2)判斷并證明函數(shù)![]() 在區(qū)間(1,+∞)上的單調(diào)性;
在區(qū)間(1,+∞)上的單調(diào)性;
(3)若直線![]() =
=![]() (
(![]()
![]() R)與
R)與![]() 的圖象無公共點,且
的圖象無公共點,且![]() <
<![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
已知函數(shù)![]() 的圖象關于直線
的圖象關于直線![]() 對稱,且在區(qū)間
對稱,且在區(qū)間![]() 上,當
上,當![]() 時,
時,![]() 有最小值3,則在區(qū)間
有最小值3,則在區(qū)間![]() 上,當
上,當![]() ____時,
____時,![]() 有最____值為_____.
有最____值為_____.
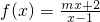 的圖象關于直線y=x對稱.
的圖象關于直線y=x對稱.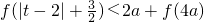 ,求實數(shù)t的取值范圍.
,求實數(shù)t的取值范圍.若R上的奇函數(shù)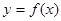 的圖象關于直線
的圖象關于直線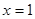 對稱,且當
對稱,且當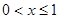 時,
時,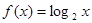 ,則方程
,則方程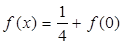 在區(qū)間
在區(qū)間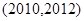 內(nèi)的所有實數(shù)根之和為( )
內(nèi)的所有實數(shù)根之和為( )
A. 4020 B.4022 C.4024 D.4026
若R上的奇函數(shù) 的圖象關于直線
的圖象關于直線 對稱,且當
對稱,且當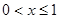 時,
時, ,則方程
,則方程 在區(qū)間
在區(qū)間 內(nèi)的所有實數(shù)根之和為( )
內(nèi)的所有實數(shù)根之和為( )
| A.4020 | B.4022 | C.4024 | D.4026 |
一、選擇題:本大題共10小題,每小題5分,共50分.
CABCA,BCDDC
二、填空題:本大題共5小題,每小題5分 ,共25分,
11. 12; 12. 學理.files/image197.gif) ; 13. 8; 14. x-2y-z+3=0; 15. ②④.
; 13. 8; 14. x-2y-z+3=0; 15. ②④.
三、解答題:本大題共6小題,共75分. 解答應寫出文字說明,證明過程或演算步驟.
16.解:(Ⅰ)
由已知 學理.files/image199.gif) , ∴
, ∴ 學理.files/image201.gif) ,
,
又 ΔABC是銳角三角形, ∴ 學理.files/image203.gif) ………………………………6分
………………………………6分
(Ⅱ) 學理.files/image205.gif)
學理.files/image207.gif)
學理.files/image209.gif)
學理.files/image211.gif) ………………………………12分
………………………………12分
17.解法一:(Ⅰ)∵學理.files/image213.gif) ,
,
且 學理.files/image215.gif) ∴
∴ 學理.files/image217.gif) , ……………………3分
, ……………………3分
∵ 學理.files/image219.gif)
∴ 學理.files/image221.gif) ……………………6分
……………………6分
(Ⅱ)取學理.files/image223.gif) 的中點
的中點學理.files/image225.gif) ,則
,則學理.files/image227.gif) ,連結
,連結學理.files/image229.gif) ,
,
∵學理.files/image231.gif) ,∴
,∴學理.files/image233.gif) ,從而
,從而學理.files/image235.gif)
作學理.files/image237.gif) ,交
,交學理.files/image239.gif) 的延長線于
的延長線于學理.files/image241.gif) ,連結
,連結學理.files/image243.gif) ,則由三垂線定理知, AC⊥MH,
,則由三垂線定理知, AC⊥MH,
從而學理.files/image245.gif) 為二面角
為二面角學理.files/image247.gif) 的平面角
…………………8分
的平面角
…………………8分
直線學理.files/image249.gif) 與直線
與直線學理.files/image251.gif) 所成的角為
所成的角為學理.files/image253.gif) ,∴
,∴學理.files/image255.gif) …………………9分
…………………9分
在學理.files/image257.gif) 中,由余弦定理得
中,由余弦定理得學理.files/image259.gif)
在學理.files/image261.gif) 中,
中,學理.files/image263.gif)
在學理.files/image265.gif) 中,
中,學理.files/image267.gif)
在學理.files/image269.gif) 中,
中,學理.files/image271.gif)
故二面角學理.files/image272.gif) 的平面角大小為
的平面角大小為學理.files/image274.gif) …………………12分
…………………12分
解法二:(Ⅰ)同解法一
學理.files/image276.jpg) (Ⅱ)在平面
(Ⅱ)在平面學理.files/image278.gif) 內(nèi),過
內(nèi),過學理.files/image280.gif) 作
作學理.files/image282.gif) ,建立空間直角坐標系
,建立空間直角坐標系學理.files/image284.gif) (如圖)
(如圖)
由題意有學理.files/image286.gif) ,設
,設學理.files/image288.gif) ,
,
則學理.files/image290.gif) ………5分
………5分
由直線學理.files/image292.gif) 與直線
與直線學理.files/image294.gif) 所成的角為
所成的角為學理.files/image296.gif) ,得
,得
學理.files/image298.gif) ,即
,即學理.files/image300.gif) ,解得
,解得學理.files/image302.gif) ………7分
………7分
∴學理.files/image304.gif) ,設平面
,設平面學理.files/image306.gif) 的一個法向量為
的一個法向量為學理.files/image308.gif) ,
,
則學理.files/image310.gif) ,取
,取學理.files/image312.gif) ,得
,得學理.files/image314.gif) ……………9分
……………9分
又 平面學理.files/image278.gif) 的法向量取為
的法向量取為學理.files/image317.gif) ……………10分
……………10分
設學理.files/image319.gif) 與
與學理.files/image321.gif) 所成的角為
所成的角為學理.files/image323.gif) ,則
,則學理.files/image325.gif) ,
,
故二面角學理.files/image272.gif) 的平面角大小為
的平面角大小為學理.files/image327.gif) ……………12分
……………12分
18. 解:(I)記“幸運觀眾獲得獎金5000元”為事件M,即前兩個問題選擇回答A、C且答對,最后在回答問題B時答錯了.
學理.files/image329.gif)
故 幸運觀眾獲得獎金5000元的概率為 學理.files/image331.gif) ………………6分
………………6分
(II) 設幸運觀眾按A→B→C順序回答問題所得獎金數(shù)為隨機變量ξ,則ξ的取值可以為0元、1000元、3000元和7000元,其分布列為
學理.files/image333.gif)
0
1000
3000
7000
P
學理.files/image334.gif)
學理.files/image336.gif)
學理.files/image338.gif)
學理.files/image340.gif)
∴ 學理.files/image342.gif) 元. ………………9分
元. ………………9分
設幸運觀眾按C→B→A順序回答問題所得獎金數(shù)為隨機變量η,則η的取值可以為0元、4000元、6000元和7000元,其分布列為
η
0
4000
6000
7000
P
學理.files/image344.gif)
學理.files/image346.gif)
學理.files/image348.gif)
學理.files/image348.gif)
∴ 學理.files/image350.gif) 元. ……11分
元. ……11分
故 乙觀眾的選擇所獲獎金期望較大. ………………12分
19.解:(1)∵ 學理.files/image352.gif) ……………………2分
……………………2分
由已知學理.files/image354.gif) 對
對學理.files/image356.gif) 恒成立,即
恒成立,即學理.files/image358.gif) 對
對學理.files/image356.gif) 恒成立
恒成立
又 學理.files/image360.gif) ∴
∴ 學理.files/image362.gif) 為所求 …………………………5分
為所求 …………………………5分
(2)取學理.files/image364.gif) , ∵
, ∵ 學理.files/image366.gif) , ∴
, ∴ 學理.files/image368.gif)
由已知學理.files/image136.gif) 在
在學理.files/image138.gif) 上是增函數(shù),即
上是增函數(shù),即學理.files/image372.gif) ,
,
也就是
學理.files/image374.gif) 即
即 學理.files/image376.gif) …………8分
…………8分
另一方面,設函數(shù)學理.files/image378.gif) ,則
,則 學理.files/image380.gif)
∴
學理.files/image382.gif) 在
在學理.files/image384.gif) 上是增函數(shù),又
上是增函數(shù),又學理.files/image386.gif)
∴
當學理.files/image388.gif) 時,
時,學理.files/image390.gif)
∴
學理.files/image392.gif) ,即
,即 學理.files/image394.gif)
學理.files/image396.gif) 綜上所述,
綜上所述,學理.files/image144.gif) ………………………………………………13分
………………………………………………13分
20.解:(Ⅰ) 由題意可知,平面區(qū)域學理.files/image398.gif) 如圖陰影所示. …3分
如圖陰影所示. …3分
設動點為學理.files/image400.gif) ,則
,則
學理.files/image402.gif) ,即
,即學理.files/image404.gif) .
.
由 學理.files/image406.gif) 知
知學理.files/image408.gif) ,x-y<0,即x2-y2<0.
,x-y<0,即x2-y2<0.
所以 y2-x2=4(y>0),即為曲線學理.files/image280.gif) 的方程 …………6分
的方程 …………6分
(Ⅱ)設學理.files/image411.gif) ,
,學理.files/image413.gif) ,則以線段
,則以線段學理.files/image415.gif) 為直徑的圓的圓心為
為直徑的圓的圓心為學理.files/image417.gif) .
.
因為以線段學理.files/image415.gif) 為直徑的圓
為直徑的圓學理.files/image419.gif) 與
與學理.files/image421.gif) 軸相切,所以半徑
軸相切,所以半徑 學理.files/image423.gif) ,
,
即 學理.files/image425.gif) ………………………8分
………………………8分
因為直線AB過點學理.files/image427.gif) ,當AB ^ x軸時,不合題意.
,當AB ^ x軸時,不合題意.
所以設直線AB的方程為 y=k(x-2).
代入雙曲線方程y2-x2=4 (y>0)得: (k2-1)x2-4k2x+(8k2-4)=0.
因為直線l與雙曲線交于A,B兩點,所以k≠±1.于是
x1+x2=,x1x2=.
∴ |AB|=學理.files/image429.gif)
∴ 學理.files/image431.gif)
化簡得:k4+2k2-1=0 ……………………………11分
解得: k2=-1 (k2=--1不合題意,舍去).
由△=(4k2)2-4(k2-1)(8k2-4)=3k2-1>0,又由于y>0,所以-1<k<- .
所以直線l存在,其斜率為 k=-. …………………13分
21. 解:(1) 因為 學理.files/image433.gif) ,所以
,所以學理.files/image435.gif) ,
,
于是: 學理.files/image437.gif) , 即
, 即學理.files/image439.gif) 是以2為公比的等比數(shù)列.
是以2為公比的等比數(shù)列.