
題目列表(包括答案和解析)
銳角三角形的內角![]() 、
、![]() 滿足
滿足![]() ,則有 ( )
,則有 ( )
(A)![]() ;(B)
;(B)![]() ;
;
(C)![]() ; D)
; D)![]() .
.
銳角三角形的內角![]() 、
、![]() 滿足
滿足![]() ,則有 ( )
,則有 ( )
(A)![]() ;(B)
;(B)![]() ;
;
(C)![]() ; D)
; D)![]() .
.
銳角三角形的內角 、
、 滿足
滿足 ,則有
( )
,則有
( )
A、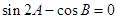 ; B、
; B、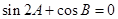 ;
;
C、 ; D、
; D、 .
.
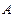 、
、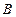 滿足
滿足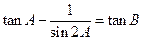 ,則有( )
,則有( )A.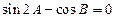 ; ; | B.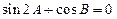 ; ; |
C.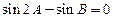 ; ; | D.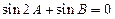 . . |
(05年全國卷Ⅱ理)銳角三角形的內角![]() 、
、![]() 滿足
滿足![]() ,則有
,則有
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
一.選擇題:DABDA CDCBC
解析:1:由條件“函數(shù)是奇函數(shù)”可排除(B)、(C), 又 在區(qū)間
在區(qū)間 上不是單調遞減, 可淘汰(A),所以選(D).
上不是單調遞減, 可淘汰(A),所以選(D).
2:取滿足題設的特殊數(shù)值 a= ,
, ,
,
0> ,檢驗不等式(B),(C),(D)均不成立,選 (A).
,檢驗不等式(B),(C),(D)均不成立,選 (A).
3:由已知得

4:把x=1代入不等式組驗算得x=1是不等式組的解,則排除(B)、(C), 再把x=-3代入不等式組驗算得x=-3是不等式組的解,則排除(B),所以選(D).
5:本題學生很容易去分母得 ,然后解方程,不易實現(xiàn)目標。
,然后解方程,不易實現(xiàn)目標。
事實上,只要利用數(shù)形結合的思想,分別畫出 的圖象,容易發(fā)現(xiàn)在第一象限沒有交點。故選A。
的圖象,容易發(fā)現(xiàn)在第一象限沒有交點。故選A。
6:當m=0時,顯然有 ;若
;若 時,由
時,由 ,得
,得
 ,方程無解,m不存在。故選C。
,方程無解,m不存在。故選C。
7:由已知不妨設長 寬
寬 高
高 ,則對角線的長為
,則對角線的長為 .故選
.故選
8:由 得sin(x-
得sin(x- )>0,即2 kπ<x-
)>0,即2 kπ<x- <2kπ+π,取k=0即知選C.
<2kπ+π,取k=0即知選C.
9:用特值法:當n=2時,代入得C +C
+C =2,排除答案A、C;當n=4時,代入得C
=2,排除答案A、C;當n=4時,代入得C +C
+C +C
+C =8,排除答案D。所以選B。
=8,排除答案D。所以選B。
10:考慮由P0射到BC的中點上,這樣依次反射最終回到P0,此時容易求出tan =
= ,由題設條件知,1<x4<2,則tan
,由題設條件知,1<x4<2,則tan ≠
≠ ,排除A、B、D,故選C.
,排除A、B、D,故選C.
二.填空題:11、1;12、-1;13、23; 14、 ;15、
;15、 ;
;
解析:
11: 將已知方程變形為  ,
,
解這個一元二次方程,得

顯然有 , 而
, 而 ,于是
,于是
原式= =
= =
=
12: 由條件得 ,其中
,其中 .
.

 是已知函數(shù)的對稱軸,
是已知函數(shù)的對稱軸,
 , 即
, 即  ,
,
于是  故應填
故應填  .
.
13:因為正方體是對稱的幾何體,所以四邊形BFD1E在該正方體的面上的射影可分為:上下、左右、前后三個方向的射影,也就是在面ABCD、面ABB1A1、面ADD1A1上的射影.
四邊形BFD1E在面ABCD和面ABB1A1上的射影相同,如圖2所示;
四邊形BFD1E在該正方體對角面的ABC1D1內,它在面ADD1A1上的射影顯然是一條線段,如圖3所示. 故應填23.
14.(略)
15.解:由條件不難得 為等腰直角三角形,設圓的半徑為1,則
為等腰直角三角形,設圓的半徑為1,則 ,
, ,
,

 ,
,
 sin∠ACO=
sin∠ACO= )=
)=
三.解答題:
16.解:(1)將 ,
, 代入函數(shù)
代入函數(shù) 得
得 ,因為
,因為 ,所以
,所以 .
------------------2分
.
------------------2分
又因為 ,
, ,
, ,所以
,所以 ,
,
因此 .
------------------5分
.
------------------5分
(2)因為點 ,
, 是
是 的中點,
的中點, , 所以點
, 所以點 的坐標為
的坐標為 . ------------------7分
. ------------------7分
又因為點 在
在 的圖象上,
的圖象上,
所以 .------------------9分
.------------------9分
因為 ,所以
,所以 ,
,
從而得 或
或 .即
.即 或
或 ------------------12分
------------------12分
17.解:(Ⅰ)設“甲投球一次命中”為事件A,“乙投球一次命中”為事件B
由題意得  , 解得
, 解得 或
或 (舍去),
(舍去),
所以乙投球的命中率為 ------------------3分
------------------3分
(Ⅱ)由題設和(Ⅰ)知 -------------4分
-------------4分
 可能的取值為0,1,2,3,故
可能的取值為0,1,2,3,故 


 ,
, 
 的分布列為
的分布列為

0
1
2
3





 的數(shù)學期望
的數(shù)學期望 ------------------12分
------------------12分
18.解:(1)∵
 -------------------------------------------------1分
-------------------------------------------------1分
當 時,
時,
∴函數(shù) 在
在 上為增函數(shù)-----------------------------------------3分
上為增函數(shù)-----------------------------------------3分
∴ ,
, --------------------------4分
--------------------------4分
(2)證明:令
則
∵當 時
時 ,∴函數(shù)
,∴函數(shù) 在區(qū)間
在區(qū)間 上為減函數(shù)
上為減函數(shù)
∴
即在 上,
上,
∴在區(qū)間 上,函數(shù)
上,函數(shù) 的圖象在函數(shù)
的圖象在函數(shù) 的圖象的下方-----8分
的圖象的下方-----8分
(3)證明:∵
當 時,不等式顯然成立
時,不等式顯然成立
當 時
時
∵ =
= -----①
-----①

 -------------②-----10分
-------------②-----10分
①+②得

≥ (當且僅當
(當且僅當 時“=”成立)---------------13分
時“=”成立)---------------13分
∴當 時,不等式成立
時,不等式成立
綜上所述得 ≥
≥
 .--------------------------14分
.--------------------------14分
19.解:(Ⅰ)設 的坐標為
的坐標為 ,則
,則 且
且 .
.
解得 , 因此,點
, 因此,點  的坐標為
的坐標為 .
.
(Ⅱ) ,根據(jù)橢圓定義,
,根據(jù)橢圓定義,
得
 ,
,
 ,
, . ∴所求橢圓方程為
. ∴所求橢圓方程為 .
.
(Ⅲ) ,
, 橢圓的準線方程為
橢圓的準線方程為 .
.
設點 的坐標為
的坐標為
 ,
, 表示點
表示點 到
到 的距離,
的距離, 表示點
表示點 到橢圓的右準線的距離.
到橢圓的右準線的距離.
則 ,
, .
.
 , 令
, 令
 ,則
,則 ,
,
 當
當 ,
, ,
,  ,
, .
.
∴  在
在 時取得最小值.
時取得最小值.
因此, 最小值=
最小值= ,此時點
,此時點 的坐標為
的坐標為 -----------------14分
-----------------14分
20.解:(Ⅰ)取 中點
中點 ,連結
,連結 .
.
 為正三角形,
為正三角形, .
.
 在正三棱柱
在正三棱柱 中,平面
中,平面 平面
平面 ,
,  平面
平面 .
.
 取
取 中點
中點 ,以
,以 為原點,
為原點, ,
, ,
, 的方向為
的方向為 軸的正方向建立空間直角坐標系,則
軸的正方向建立空間直角坐標系,則 ,
, ,
, ,
, ,
,  ,
,
 ,
, ,
, .
.
 ,
, ,
,
 ,
, .
.
 平面
平面 .--------------------6分
.--------------------6分
(Ⅱ)設平面 的法向量為
的法向量為 .
.
 ,
, .
.  ,
, ,
,



令 得
得 為平面
為平面 的一個法向量.--------------------9分
的一個法向量.--------------------9分
由(Ⅰ)知 平面
平面 ,
,  為平面
為平面 的法向量.
的法向量.
 ,
, .
.
 二面角
二面角 的大小為
的大小為 . --------------------11分
. --------------------11分
(Ⅲ) 中,
中, ,
, .
.
在正三棱柱中, 到平面
到平面 的距離為
的距離為 .設點
.設點 到平面
到平面 的距離為
的距離為 .
.
由 得
得 ,
,  .
.
 點
點 到平面
到平面 的距離為
的距離為 --------------------14分
--------------------14分
21.解(1)∵不等式 ≤0的解集有且只有一個元素
≤0的解集有且只有一個元素
∴ 解得
解得 或
或 --------------------2分
--------------------2分
當 時函數(shù)
時函數(shù) 在
在 遞增,不滿足條件②--------------------3分
遞增,不滿足條件②--------------------3分
當 時函數(shù)
時函數(shù) 在(0,2)上遞減,滿足條件②--------------------4分
在(0,2)上遞減,滿足條件②--------------------4分
綜上得 ,即
,即 --------------------5分
--------------------5分
(2)由(1)知 , 當
, 當 時,
時,
當 ≥2時
≥2時 =
= =
= --------------------7分
--------------------7分
∴ --------------------8分
--------------------8分
(3)由題設可得 --------------------9分
--------------------9分
∵ ,
, ,
,
∴ ,
, 都滿足
都滿足 --------------------11分
--------------------11分
∵當 ≥3時,
≥3時,

即當 ≥3時,數(shù)列{
≥3時,數(shù)列{ }遞增,
}遞增,
∵
 ,由
,由
 ,可知
,可知 滿足
滿足 ----------------13分
----------------13分
∴數(shù)列{ }的變號數(shù)為3. ------------------14分
}的變號數(shù)為3. ------------------14分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com