
題目列表(包括答案和解析)
關(guān)于函數(shù)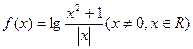 有下列命題:
有下列命題:
①函數(shù)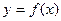 的圖象關(guān)于y軸對稱 ②在
的圖象關(guān)于y軸對稱 ②在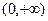 上
上 是增函數(shù);在
是增函數(shù);在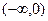 上
上 是減函數(shù) ③函數(shù)
是減函數(shù) ③函數(shù) 的最小值是
的最小值是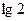 ④在
④在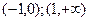 上
上 為增函數(shù)
為增函數(shù)
⑤ 無最大值,也無最小值 ,其中正確命題的序號是_________
無最大值,也無最小值 ,其中正確命題的序號是_________
關(guān)于函數(shù)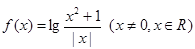 有下列命題:①函數(shù)
有下列命題:①函數(shù)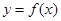 的圖像關(guān)于y軸對稱;②在區(qū)間(-∞,0)上,函數(shù)
的圖像關(guān)于y軸對稱;②在區(qū)間(-∞,0)上,函數(shù)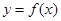 是減函數(shù);③函數(shù)
是減函數(shù);③函數(shù)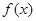 的最小值為lg2;④在區(qū)間(1,+∞)上,函數(shù)
的最小值為lg2;④在區(qū)間(1,+∞)上,函數(shù)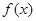 是增函數(shù)。其中是真命題的序號為
。
是增函數(shù)。其中是真命題的序號為
。
關(guān)于函數(shù)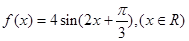 有下列命題:
有下列命題:
①由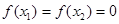 可得
可得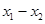 必是
必是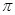 的整數(shù)倍;②
的整數(shù)倍;②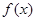 的表達式可改寫為
的表達式可改寫為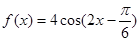 ;③
;③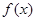 的圖象關(guān)于點
的圖象關(guān)于點 對稱;④
對稱;④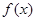 的圖象關(guān)于直線
的圖象關(guān)于直線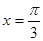 對稱;⑤
對稱;⑤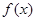 在區(qū)間
在區(qū)間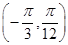 上是增函數(shù);其中正確的是( )
上是增函數(shù);其中正確的是( )
A.②③⑤ B.①② ③ C.②③ ④ D.①③⑤
關(guān)于函數(shù) 有下列命題:
有下列命題:
① 是以
是以 為最小正周期的周期函數(shù);
為最小正周期的周期函數(shù);
② 可改寫為
可改寫為 ;
;
③ 的圖象關(guān)于
的圖象關(guān)于 對稱;
對稱;
④ 的圖象關(guān)于直線
的圖象關(guān)于直線 對稱;其中正確的序號為 。
對稱;其中正確的序號為 。
關(guān)于函數(shù) 有下列命題:
有下列命題:
(1) 的表達式可改寫為
的表達式可改寫為 ;
;
(2) 是以
是以 為最小正周期的周期函數(shù);
為最小正周期的周期函數(shù);
(3) 的圖象關(guān)于點
的圖象關(guān)于點 對稱;
對稱;
(4) 的圖象關(guān)于直線
的圖象關(guān)于直線 對稱。
對稱。
其中正確的命題序號是 。
一、填空題 (每題5分)
1)2009年高考模擬考試%20數(shù)學(xué)理科.files/image134.gif) 2)
2)2009年高考模擬考試%20數(shù)學(xué)理科.files/image136.gif) 3)0 4)
3)0 4) 2009年高考模擬考試%20數(shù)學(xué)理科.files/image138.gif) 5)
5)2009年高考模擬考試%20數(shù)學(xué)理科.files/image140.gif) 6)
6) 2009年高考模擬考試%20數(shù)學(xué)理科.files/image142.gif) 7)②④ 8)
7)②④ 8)2009年高考模擬考試%20數(shù)學(xué)理科.files/image144.gif) 9)
9)2009年高考模擬考試%20數(shù)學(xué)理科.files/image146.gif) 10)
10)2009年高考模擬考試%20數(shù)學(xué)理科.files/image148.gif) 11)7
11)7
二、選擇題(每題5分)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image089.jpg) 12、A 13、B 14、D 15、D
12、A 13、B 14、D 15、D
三、解答題
16、16、
(1)因為2009年高考模擬考試%20數(shù)學(xué)理科.files/image150.gif) ,所以∠BCA(或其補角)即為異面直線
,所以∠BCA(或其補角)即為異面直線2009年高考模擬考試%20數(shù)學(xué)理科.files/image152.gif) 與
與2009年高考模擬考試%20數(shù)學(xué)理科.files/image154.gif) 所成角
-------(3分)
所成角
-------(3分)
∠ABC=90°, AB=BC=1,所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image156.gif) , -------(2分)
, -------(2分)
即異面直線2009年高考模擬考試%20數(shù)學(xué)理科.files/image152.gif) 與
與2009年高考模擬考試%20數(shù)學(xué)理科.files/image154.gif) 所成角大小為
所成角大小為2009年高考模擬考試%20數(shù)學(xué)理科.files/image024.gif) 。
-------(1分)
。
-------(1分)
(2)直三棱柱ABC-A1B2009年高考模擬考試%20數(shù)學(xué)理科.files/image159.gif) ,所以
,所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image161.gif) 即為直線A
即為直線A2009年高考模擬考試%20數(shù)學(xué)理科.files/image163.gif) 。 -------(2分)
。 -------(2分)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image165.gif) 中,AB=BC=1得到
中,AB=BC=1得到2009年高考模擬考試%20數(shù)學(xué)理科.files/image167.gif) ,
,2009年高考模擬考試%20數(shù)學(xué)理科.files/image169.gif) 中,得到
中,得到2009年高考模擬考試%20數(shù)學(xué)理科.files/image171.gif) , -------(2分)
, -------(2分)
所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image173.gif) -------(2分)
-------(2分)
17、2009年高考模擬考試%20數(shù)學(xué)理科.files/image175.gif) -------(1分)
-------(1分)
=2009年高考模擬考試%20數(shù)學(xué)理科.files/image177.gif) -------(1分)
-------(1分)
=2009年高考模擬考試%20數(shù)學(xué)理科.files/image179.gif) -------(1分)
-------(1分)
若2009年高考模擬考試%20數(shù)學(xué)理科.files/image095.gif) 為其圖象對稱中心的橫坐標(biāo),即
為其圖象對稱中心的橫坐標(biāo),即2009年高考模擬考試%20數(shù)學(xué)理科.files/image182.gif) =0, -------(1分)
=0, -------(1分)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image184.gif) , -------(1分)
, -------(1分)
解得:2009年高考模擬考試%20數(shù)學(xué)理科.files/image186.gif) -------(1分)
-------(1分)
(2)2009年高考模擬考試%20數(shù)學(xué)理科.files/image188.gif) , -------(2分)
, -------(2分)
即2009年高考模擬考試%20數(shù)學(xué)理科.files/image190.gif) ,而
,而2009年高考模擬考試%20數(shù)學(xué)理科.files/image192.gif) ,所以
,所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image194.gif) 。
-------(2分)
。
-------(2分)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image196.gif) ,
,2009年高考模擬考試%20數(shù)學(xué)理科.files/image198.gif) , -------(2分)
, -------(2分)
所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image200.gif) ------(2分)
------(2分)
18、2009年高考模擬考試%20數(shù)學(xué)理科.files/image202.gif) ,顧客得到的優(yōu)惠率是
,顧客得到的優(yōu)惠率是2009年高考模擬考試%20數(shù)學(xué)理科.files/image204.gif) 。 -------(5分)
。 -------(5分)
(2)、設(shè)商品的標(biāo)價為x元,則500≤x≤800 ----- -(2分)
消費金額: 400≤0.8x≤640
由題意可得:
(1)2009年高考模擬考試%20數(shù)學(xué)理科.files/image205.jpg) ≥
≥2009年高考模擬考試%20數(shù)學(xué)理科.files/image206.jpg) 無解
------(3分)
無解
------(3分)
或(2)2009年高考模擬考試%20數(shù)學(xué)理科.files/image207.jpg) ≥
≥2009年高考模擬考試%20數(shù)學(xué)理科.files/image206.jpg) 得:625≤x≤750 ------(3分)
得:625≤x≤750 ------(3分)
因此,當(dāng)顧客購買標(biāo)價在2009年高考模擬考試%20數(shù)學(xué)理科.files/image208.jpg) 元內(nèi)的商品時,可得到不小于
元內(nèi)的商品時,可得到不小于2009年高考模擬考試%20數(shù)學(xué)理科.files/image206.jpg) 的優(yōu)惠率。------(1分)
的優(yōu)惠率。------(1分)
19、(1)y=2009年高考模擬考試%20數(shù)學(xué)理科.files/image209.jpg) ?
?2009年高考模擬考試%20數(shù)學(xué)理科.files/image210.jpg) =(2x-b)+(b+1)=2x+1
-----(1分)
=(2x-b)+(b+1)=2x+1
-----(1分)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image212.gif) 與
與2009年高考模擬考試%20數(shù)學(xué)理科.files/image095.gif) 軸的交點
軸的交點2009年高考模擬考試%20數(shù)學(xué)理科.files/image215.gif) 為
為2009年高考模擬考試%20數(shù)學(xué)理科.files/image217.gif) ,所以
,所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image219.gif) ;
-----(1分)
;
-----(1分)
所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image221.gif) ,即
,即2009年高考模擬考試%20數(shù)學(xué)理科.files/image223.gif) ,
-----(1分)
,
-----(1分)
因為2009年高考模擬考試%20數(shù)學(xué)理科.files/image225.gif) 在
在2009年高考模擬考試%20數(shù)學(xué)理科.files/image212.gif) 上,所以
上,所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image227.gif) ,即
,即2009年高考模擬考試%20數(shù)學(xué)理科.files/image229.gif) -----(1分)
-----(1分)
(2)設(shè)2009年高考模擬考試%20數(shù)學(xué)理科.files/image231.gif)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image233.gif) (
(2009年高考模擬考試%20數(shù)學(xué)理科.files/image235.gif) ),
),
即2009年高考模擬考試%20數(shù)學(xué)理科.files/image237.gif)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image233.gif) (
(2009年高考模擬考試%20數(shù)學(xué)理科.files/image235.gif) ) ----(1分)
) ----(1分)
(A)當(dāng)2009年高考模擬考試%20數(shù)學(xué)理科.files/image241.gif) 時,
時,2009年高考模擬考試%20數(shù)學(xué)理科.files/image243.gif)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image245.gif) ----(1分)
----(1分)
=2009年高考模擬考試%20數(shù)學(xué)理科.files/image247.gif) =
=2009年高考模擬考試%20數(shù)學(xué)理科.files/image249.gif) ,而
,而2009年高考模擬考試%20數(shù)學(xué)理科.files/image251.gif) ,所以
,所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image253.gif) ----(1分)
----(1分)
(B)當(dāng)2009年高考模擬考試%20數(shù)學(xué)理科.files/image255.gif) 時,
時,2009年高考模擬考試%20數(shù)學(xué)理科.files/image257.gif) ----(1分)
----(1分)
= 2009年高考模擬考試%20數(shù)學(xué)理科.files/image259.gif) =
=2009年高考模擬考試%20數(shù)學(xué)理科.files/image261.gif) ,
----(1分)
,
----(1分)
而2009年高考模擬考試%20數(shù)學(xué)理科.files/image263.gif) ,所以
,所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image265.gif) ----(1分)
----(1分)
因此2009年高考模擬考試%20數(shù)學(xué)理科.files/image267.gif) (
(2009年高考模擬考試%20數(shù)學(xué)理科.files/image235.gif) )
----(1分)
)
----(1分)
(3)假設(shè)2009年高考模擬考試%20數(shù)學(xué)理科.files/image126.gif) ,使得
,使得2009年高考模擬考試%20數(shù)學(xué)理科.files/image128.gif) ,
,
(A)2009年高考模擬考試%20數(shù)學(xué)理科.files/image269.gif) 為奇數(shù)
為奇數(shù)
(一)2009年高考模擬考試%20數(shù)學(xué)理科.files/image130.gif) 為奇數(shù),則
為奇數(shù),則2009年高考模擬考試%20數(shù)學(xué)理科.files/image272.gif) 為偶數(shù)。則
為偶數(shù)。則2009年高考模擬考試%20數(shù)學(xué)理科.files/image274.gif) ,
,2009年高考模擬考試%20數(shù)學(xué)理科.files/image276.gif) 。則
。則2009年高考模擬考試%20數(shù)學(xué)理科.files/image278.gif) ,解得:
,解得:2009年高考模擬考試%20數(shù)學(xué)理科.files/image280.gif) 與
與2009年高考模擬考試%20數(shù)學(xué)理科.files/image235.gif) 矛盾。
----(1分)
矛盾。
----(1分)
(二)2009年高考模擬考試%20數(shù)學(xué)理科.files/image130.gif) 為偶數(shù),則
為偶數(shù),則2009年高考模擬考試%20數(shù)學(xué)理科.files/image272.gif) 為奇數(shù)。則
為奇數(shù)。則2009年高考模擬考試%20數(shù)學(xué)理科.files/image283.gif) ,
,2009年高考模擬考試%20數(shù)學(xué)理科.files/image285.gif) 。則
。則2009年高考模擬考試%20數(shù)學(xué)理科.files/image287.gif) ,解得:
,解得:2009年高考模擬考試%20數(shù)學(xué)理科.files/image289.gif) (
(2009年高考模擬考試%20數(shù)學(xué)理科.files/image291.gif) 是正偶數(shù))。 ----(1分)
是正偶數(shù))。 ----(1分)
(B)2009年高考模擬考試%20數(shù)學(xué)理科.files/image269.gif) 為偶數(shù)
為偶數(shù)
(一)2009年高考模擬考試%20數(shù)學(xué)理科.files/image130.gif) 為奇數(shù),則
為奇數(shù),則2009年高考模擬考試%20數(shù)學(xué)理科.files/image272.gif) 為奇數(shù)。則
為奇數(shù)。則2009年高考模擬考試%20數(shù)學(xué)理科.files/image274.gif) ,
,2009年高考模擬考試%20數(shù)學(xué)理科.files/image285.gif) 。則
。則2009年高考模擬考試%20數(shù)學(xué)理科.files/image294.gif) ,解得:
,解得:2009年高考模擬考試%20數(shù)學(xué)理科.files/image296.gif) (
(2009年高考模擬考試%20數(shù)學(xué)理科.files/image298.gif) 是正奇數(shù))。
----(1分)
是正奇數(shù))。
----(1分)
(二)2009年高考模擬考試%20數(shù)學(xué)理科.files/image130.gif) 為偶數(shù),則
為偶數(shù),則2009年高考模擬考試%20數(shù)學(xué)理科.files/image272.gif) 為偶數(shù)。則
為偶數(shù)。則2009年高考模擬考試%20數(shù)學(xué)理科.files/image283.gif) ,
,2009年高考模擬考試%20數(shù)學(xué)理科.files/image276.gif) 。則
。則2009年高考模擬考試%20數(shù)學(xué)理科.files/image301.gif) ,解得:
,解得:2009年高考模擬考試%20數(shù)學(xué)理科.files/image303.gif) 與
與2009年高考模擬考試%20數(shù)學(xué)理科.files/image235.gif) 矛盾。 ----(1分)
矛盾。 ----(1分)
由此得:對于給定常數(shù)m(2009年高考模擬考試%20數(shù)學(xué)理科.files/image124.gif) ),這樣的
),這樣的2009年高考模擬考試%20數(shù)學(xué)理科.files/image130.gif) 總存在;當(dāng)
總存在;當(dāng)2009年高考模擬考試%20數(shù)學(xué)理科.files/image269.gif) 是奇數(shù)時,
是奇數(shù)時,2009年高考模擬考試%20數(shù)學(xué)理科.files/image289.gif) ;當(dāng)
;當(dāng)2009年高考模擬考試%20數(shù)學(xué)理科.files/image269.gif) 是偶數(shù)時,
是偶數(shù)時,2009年高考模擬考試%20數(shù)學(xué)理科.files/image296.gif) 。
----(1分)
。
----(1分)
20、(1)解法(A):點P與點F(2,0)的距離比它到直線2009年高考模擬考試%20數(shù)學(xué)理科.files/image095.gif) +4=0的距離小2,所以點P與點F(2,0)的距離與它到直線
+4=0的距離小2,所以點P與點F(2,0)的距離與它到直線2009年高考模擬考試%20數(shù)學(xué)理科.files/image095.gif) +2=0的距離相等。 ----(1分)
+2=0的距離相等。 ----(1分)
由拋物線定義得:點2009年高考模擬考試%20數(shù)學(xué)理科.files/image309.gif) 在以
在以2009年高考模擬考試%20數(shù)學(xué)理科.files/image311.gif) 為焦點直線
為焦點直線2009年高考模擬考試%20數(shù)學(xué)理科.files/image095.gif) +2=0為準(zhǔn)線的拋物線上, ----(1分)
+2=0為準(zhǔn)線的拋物線上, ----(1分)
拋物線方程為2009年高考模擬考試%20數(shù)學(xué)理科.files/image313.gif) 。 ----(2分)
。 ----(2分)
解法(B):設(shè)動點2009年高考模擬考試%20數(shù)學(xué)理科.files/image315.gif) ,則
,則2009年高考模擬考試%20數(shù)學(xué)理科.files/image317.gif) 。當(dāng)
。當(dāng)2009年高考模擬考試%20數(shù)學(xué)理科.files/image319.gif) 時,
時,2009年高考模擬考試%20數(shù)學(xué)理科.files/image321.gif) ,化簡得:
,化簡得:2009年高考模擬考試%20數(shù)學(xué)理科.files/image323.gif) ,顯然
,顯然2009年高考模擬考試%20數(shù)學(xué)理科.files/image325.gif) ,而
,而2009年高考模擬考試%20數(shù)學(xué)理科.files/image319.gif) ,此時曲線不存在。當(dāng)
,此時曲線不存在。當(dāng)2009年高考模擬考試%20數(shù)學(xué)理科.files/image136.gif) 時,
時,2009年高考模擬考試%20數(shù)學(xué)理科.files/image328.gif) ,化簡得:
,化簡得:2009年高考模擬考試%20數(shù)學(xué)理科.files/image313.gif) 。
。
(2)2009年高考模擬考試%20數(shù)學(xué)理科.files/image330.gif) ,
,
2009年高考模擬考試%20數(shù)學(xué)理科.files/image332.gif) ,
,
2009年高考模擬考試%20數(shù)學(xué)理科.files/image334.gif) ,
----(1分)
,
----(1分)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image336.gif) ,
,
2009年高考模擬考試%20數(shù)學(xué)理科.files/image338.gif) ,即
,即2009年高考模擬考試%20數(shù)學(xué)理科.files/image340.gif) ,
,2009年高考模擬考試%20數(shù)學(xué)理科.files/image342.gif) ,
----(2分)
,
----(2分)
直線為2009年高考模擬考試%20數(shù)學(xué)理科.files/image344.gif) ,所以
,所以2009年高考模擬考試%20數(shù)學(xué)理科.files/image346.gif) ----(1分)
----(1分)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image348.gif)
2009年高考模擬考試%20數(shù)學(xué)理科.files/image350.gif) ----(1分)
----(1分)
由(a)(b)得:直線恒過定點2009年高考模擬考試%20數(shù)學(xué)理科.files/image352.gif) 。
----(1分)
。
----(1分)
1、(逆命題)如果直線2009年高考模擬考試%20數(shù)學(xué)理科.files/image346.gif) ,且與拋物線
,且與拋物線2009年高考模擬考試%20數(shù)學(xué)理科.files/image313.gif) 相交于A、B兩點,O為坐標(biāo)原點。求證:OA⊥OB (評分:提出問題得1分,解答正確得1分)
相交于A、B兩點,O為坐標(biāo)原點。求證:OA⊥OB (評分:提出問題得1分,解答正確得1分)
(若,求證:2009年高考模擬考試%20數(shù)學(xué)理科.files/image353.jpg) ?
?2009年高考模擬考試%20數(shù)學(xué)理科.files/image354.jpg) =0,得分相同)
=0,得分相同)
2、(簡單推廣命題)如果直線L與拋物線2009年高考模擬考試%20數(shù)學(xué)理科.files/image355.jpg) =2px(p>0)相交于A、B兩點,且OA⊥OB。求證:直線L過定點(2p,0)
=2px(p>0)相交于A、B兩點,且OA⊥OB。求證:直線L過定點(2p,0)
或:它的逆命題(評分:提出問題得2分,解答正確得1分)
3、(類比)
3.1(1)如果直線L與橢圓2009年高考模擬考試%20數(shù)學(xué)理科.files/image356.jpg) +
+2009年高考模擬考試%20數(shù)學(xué)理科.files/image357.jpg) =1(a>b>0)相交于A、B兩點,M是其右頂點,當(dāng)MA⊥MB。求證:直線L過定點(
=1(a>b>0)相交于A、B兩點,M是其右頂點,當(dāng)MA⊥MB。求證:直線L過定點(2009年高考模擬考試%20數(shù)學(xué)理科.files/image358.jpg) ,0)
,0)
3.1(2)如果直線L與橢圓2009年高考模擬考試%20數(shù)學(xué)理科.files/image356.jpg) +
+2009年高考模擬考試%20數(shù)學(xué)理科.files/image357.jpg) =1(a>b>0)相交于A、B兩點,M是其左頂點,當(dāng)MA⊥MB。求證:直線L過定點(
=1(a>b>0)相交于A、B兩點,M是其左頂點,當(dāng)MA⊥MB。求證:直線L過定點(2009年高考模擬考試%20數(shù)學(xué)理科.files/image359.jpg) ,0)
,0)
3.1(3)或它的逆命題
3.2(1)如果直線L與雙曲線2009年高考模擬考試%20數(shù)學(xué)理科.files/image360.jpg) -
-2009年高考模擬考試%20數(shù)學(xué)理科.files/image361.jpg) =1(a>0,b>0)相交于A、B兩點,M是其右頂點,當(dāng)MA⊥MB。求證:直線L過定點(
=1(a>0,b>0)相交于A、B兩點,M是其右頂點,當(dāng)MA⊥MB。求證:直線L過定點(2009年高考模擬考試%20數(shù)學(xué)理科.files/image362.jpg) ,0)(a≠b)
,0)(a≠b)
3.2(2)如果直線L與雙曲線2009年高考模擬考試%20數(shù)學(xué)理科.files/image360.jpg) -
-2009年高考模擬考試%20數(shù)學(xué)理科.files/image361.jpg) =1(a>0,b>0)相交于A、B兩點,M是其左頂點,當(dāng)MA⊥MB。求證:直線L過定點(
=1(a>0,b>0)相交于A、B兩點,M是其左頂點,當(dāng)MA⊥MB。求證:直線L過定點(2009年高考模擬考試%20數(shù)學(xué)理科.files/image363.jpg) ,0)(a≠b)
,0)(a≠b)
3.2(3)或它的逆命題
(評分:提出問題得3分,解答正確得3分)
4、(再推廣)
直角頂點在圓錐曲線上運動
如:如果直線L與拋物線2009年高考模擬考試%20數(shù)學(xué)理科.files/image355.jpg) =2px(p>0)相交于A、B兩點,P是拋物線上一定點(
=2px(p>0)相交于A、B兩點,P是拋物線上一定點(2009年高考模擬考試%20數(shù)學(xué)理科.files/image364.jpg) ,
,2009年高考模擬考試%20數(shù)學(xué)理科.files/image365.jpg) ),且PA⊥PB。求證:直線L過定點(
),且PA⊥PB。求證:直線L過定點(2009年高考模擬考試%20數(shù)學(xué)理科.files/image364.jpg) +2p,-
+2p,-2009年高考模擬考試%20數(shù)學(xué)理科.files/image365.jpg) )
)
(評分:提出問題得4分,解答正確得3分)
5、(再推廣)
如果直線L與拋物線2009年高考模擬考試%20數(shù)學(xué)理科.files/image355.jpg) =2px(p>0)相交于A、B兩點,P是拋物線上一定點(
=2px(p>0)相交于A、B兩點,P是拋物線上一定點(2009年高考模擬考試%20數(shù)學(xué)理科.files/image364.jpg) ,
,2009年高考模擬考試%20數(shù)學(xué)理科.files/image365.jpg) ),PA與PB的斜率乘積是常數(shù)m。求證:直線L過定點(
),PA與PB的斜率乘積是常數(shù)m。求證:直線L過定點(2009年高考模擬考試%20數(shù)學(xué)理科.files/image364.jpg) -
-2009年高考模擬考試%20數(shù)學(xué)理科.files/image366.jpg) ,-
,-2009年高考模擬考試%20數(shù)學(xué)理科.files/image365.jpg) )
)
(評分:提出問題得5分,解答正確得4分)
或2009年高考模擬考試%20數(shù)學(xué)理科.files/image367.jpg) ?
?2009年高考模擬考試%20數(shù)學(xué)理科.files/image368.jpg) 為常數(shù)
為常數(shù)
頂點在圓錐曲線上運動并把直角改為一般定角或OA與OB的斜率乘積是常數(shù)或2009年高考模擬考試%20數(shù)學(xué)理科.files/image353.jpg) ?
?2009年高考模擬考試%20數(shù)學(xué)理科.files/image354.jpg) 為常數(shù)
為常數(shù)
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com