
題目列表(包括答案和解析)
(22) (本小題滿分14分)
如圖,橢圓![]() (a>b>0)的一個焦點為F(1,0),且過點(2,0).
(a>b>0)的一個焦點為F(1,0),且過點(2,0).
(Ⅰ)求橢圓C的方程;
(Ⅱ)若AB為垂直于x軸的動弦,直線l:x=4與x軸交于點N,直線AF與BN交于點M.
(ⅰ)求證:點M恒在橢圓C上;
(ⅱ)求△AMN面積的最大值.

(本小題12分)
已知某商品的價格 (元)與需求量
(元)與需求量 (件)之間的關系有如下一組數(shù)據(jù):
(件)之間的關系有如下一組數(shù)據(jù):
|
|
14 |
16 |
18 |
20 |
22 |
|
|
12 |
10 |
7 |
5 |
3 |
(1)畫出 關于
關于 的散點圖
的散點圖
(2)用最小二乘法求出回歸直線方程
(3)計算 的值,并說明回歸模型擬合程度的好壞。
的值,并說明回歸模型擬合程度的好壞。
(本小題12分)
已知某商品的價格 (元)與需求量
(元)與需求量 (件)之間的關系有如下一組數(shù)據(jù):
(件)之間的關系有如下一組數(shù)據(jù):
 | 14 | 16 | 18 | 20 | 22 |
 | 12 | 10 | 7 | 5 | 3 |
 關于
關于 的散點圖
的散點圖 的值,并說明回歸模型擬合程度的好壞。
的值,并說明回歸模型擬合程度的好壞。(本小題滿分14分)
某興趣小組欲研究晝夜溫差大小與患感冒人數(shù)多少之間的關系,他們分別到氣象局與某醫(yī)院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數(shù),得到如下資料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 晝夜溫差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就診人數(shù)y(個) | 22 | 25 | 29 | 26 | 16 | 12 |
該興趣小組確定的研究方案是:先從這六組數(shù)據(jù)中選取2組,用剩下的4組數(shù)據(jù)求線性回歸方程,再用被選取的2組數(shù)據(jù)進行檢驗.
(Ⅰ)求選取的2組數(shù)據(jù)恰好是相鄰兩個月的概率;(5分)
(Ⅱ)若選取的是1月與6月的兩組數(shù)據(jù),請根據(jù)2至5月份的數(shù)據(jù),求出y關于x的線性回歸方程![]() ;(6分)
;(6分)
(Ⅲ)若由線性回歸方程得到的估計數(shù)據(jù)與所選出的檢驗數(shù)據(jù)的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?(3分)
(參考公式:  )
)
(本小題滿分12分)在第9屆校園文化藝術節(jié)棋類比賽項目報名過程中,我校高二(2)班共有16名男生和14名女生預報名參加,調查發(fā)現(xiàn),男、女選手中分別有10人和6人會圍棋.
(I)根據(jù)以上數(shù)據(jù)完成以下2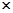 2列聯(lián)表:
2列聯(lián)表:
|
|
會圍棋 |
不會圍棋 |
總計 |
|
男 |
|
|
|
|
女 |
|
|
|
|
總計 |
|
|
30 |
并回答能否在犯錯的概率不超過0.10的前提下認為性別與會圍棋有關?
參考公式: 其中n=a+b+c+d
其中n=a+b+c+d
參考數(shù)據(jù):
|
|
0.40 |
0.25 |
0.10 |
0.010 |
|
|
0.708 |
1.323 |
2.706 |
6.635 |
(Ⅱ)若從會圍棋的選手中隨機抽取3人成立該班圍棋代表隊,則該代表隊中既有男又
有女的概率是多少?
(Ⅲ)若從14名女棋手中隨機抽取2人參加棋類比賽,記會圍棋的人數(shù)為 ,求
,求 的期望.
的期望.
一、1 B 2 D 3 A 4 D 5 C 6 B
7 A 8 A 9 C 10 D 11 C 12 B
二、13、3 14、學模擬%20(文).files/image216.gif) 15、-160 16、
15、-160 16、 學模擬%20(文).files/image218.gif)
三、17、解: (1)學模擬%20(文).files/image220.gif)
學模擬%20(文).files/image002.gif) ……… 3分
……… 3分
學模擬%20(文).files/image222.gif)
學模擬%20(文).files/image152.gif) 的最小正周期為
的最小正周期為學模擬%20(文).files/image041.gif)
學模擬%20(文).files/image002.gif) …………………
5分
…………………
5分
(2)學模擬%20(文).files/image002.gif)
學模擬%20(文).files/image225.gif) , ………………… 7分
, ………………… 7分
學模擬%20(文).files/image227.gif) …………………
10分
…………………
10分
學模擬%20(文).files/image222.gif)
學模擬%20(文).files/image229.gif)
學模擬%20(文).files/image002.gif) ………………… 11分
………………… 11分
學模擬%20(文).files/image222.gif) 當
當學模擬%20(文).files/image154.gif) 時,函數(shù)
時,函數(shù)學模擬%20(文).files/image152.gif) 的最大值為1,最小值
的最大值為1,最小值學模擬%20(文).files/image231.gif)
學模擬%20(文).files/image002.gif) ……… 12分
……… 12分
18.解:(1)P1=學模擬%20(文).files/image233.gif) ;
……… 6分
;
……… 6分
(2)方法一:P2=學模擬%20(文).files/image235.gif)
方法二:P2=學模擬%20(文).files/image237.gif)
方法三:P2=1-學模擬%20(文).files/image239.gif) ……… 12分
……… 12分
19、解法一:
(Ⅰ)連結學模擬%20(文).files/image162.gif) C交BC
C交BC學模擬%20(文).files/image242.gif) 于O,則O是B
于O,則O是B 學模擬%20(文).files/image244.gif) C的中點,連結DO。
C的中點,連結DO。
學模擬%20(文).files/image246.jpg) ∵在△A
∵在△A學模擬%20(文).files/image248.gif) C中,O、D均為中點,
C中,O、D均為中點,
∴A學模擬%20(文).files/image248.gif) ∥DO…………………………2分
∥DO…………………………2分
∵A學模擬%20(文).files/image248.gif)
學模擬%20(文).files/image250.gif) 平面B
平面B學模擬%20(文).files/image158.gif) D,DO
D,DO學模擬%20(文).files/image253.gif) 平面B
平面B學模擬%20(文).files/image158.gif) D,
D,
∴A學模擬%20(文).files/image248.gif) ∥平面B
∥平面B學模擬%20(文).files/image158.gif) D。…………………4分
D。…………………4分
(Ⅱ)設正三棱柱底面邊長為2,則DC = 1。
∵∠學模擬%20(文).files/image158.gif) DC = 60°,∴C
DC = 60°,∴C學模擬%20(文).files/image158.gif) =
= 學模擬%20(文).files/image255.gif) 。
。
作DE⊥BC于E。
∵平面BC學模擬%20(文).files/image158.gif) ⊥平面ABC,
⊥平面ABC,
∴DE⊥平面BC學模擬%20(文).files/image158.gif)
學模擬%20(文).files/image248.gif)
作EF⊥B學模擬%20(文).files/image158.gif) 于F,連結DF,則 DF⊥B
于F,連結DF,則 DF⊥B學模擬%20(文).files/image158.gif)
∴∠DFE是二面角D-B學模擬%20(文).files/image158.gif) -C的平面角………………8分
-C的平面角………………8分
在Rt△DEC中,DE=學模擬%20(文).files/image259.gif)
在Rt△BFE中,EF =
BE?sin學模擬%20(文).files/image261.gif)
∴在Rt△DEF中,tan∠DFE = 學模擬%20(文).files/image263.gif)
學模擬%20(文).files/image265.gif) ∴二面角D-B
∴二面角D-B學模擬%20(文).files/image158.gif) -C的大小為arctan
-C的大小為arctan學模擬%20(文).files/image268.gif) ………………12分
………………12分
解法二:以AC的中D為原點建立坐標系,如圖,
設| AD | = 1∵∠學模擬%20(文).files/image158.gif) DC =60°∴| C
DC =60°∴| C學模擬%20(文).files/image158.gif) |
=
|
= 學模擬%20(文).files/image255.gif) 。
。
則A(1,0,0),B(0,學模擬%20(文).files/image255.gif) ,0),C(-1,0,0),
,0),C(-1,0,0),
學模擬%20(文).files/image273.gif) (1,0
(1,0學模擬%20(文).files/image255.gif) ),
),學模擬%20(文).files/image276.gif) ,
,學模擬%20(文).files/image278.gif)
(Ⅰ)連結學模擬%20(文).files/image248.gif) C交B
C交B學模擬%20(文).files/image281.gif) 于O是
于O是學模擬%20(文).files/image248.gif) C的中點,連結DO,則
C的中點,連結DO,則
O學模擬%20(文).files/image284.gif) .
. 學模擬%20(文).files/image286.gif) =
=學模擬%20(文).files/image288.gif)
∵A學模擬%20(文).files/image248.gif)
學模擬%20(文).files/image250.gif) 平面B
平面B學模擬%20(文).files/image281.gif) D,
D,
∴A學模擬%20(文).files/image248.gif) ∥平面B
∥平面B學模擬%20(文).files/image281.gif) D.………………………………………………4分
D.………………………………………………4分
(Ⅱ)學模擬%20(文).files/image294.gif) =(-1,0,
=(-1,0,學模擬%20(文).files/image255.gif) ),
),學模擬%20(文).files/image297.gif)
設平面B學模擬%20(文).files/image281.gif) D的法向量為n = ( x , y , z ),則
D的法向量為n = ( x , y , z ),則學模擬%20(文).files/image300.gif)
即學模擬%20(文).files/image302.gif) 則有
則有學模擬%20(文).files/image304.gif) = 0令z = 1
= 0令z = 1
則n = (學模擬%20(文).files/image255.gif) ,0,1)
…………………………………8分
,0,1)
…………………………………8分
設平面BC學模擬%20(文).files/image158.gif)
學模擬%20(文).files/image248.gif) 的法向量為m = ( x′
,y′,z′)
的法向量為m = ( x′
,y′,z′)