題目列表(包括答案和解析)
(17) （本小題滿分12分）在△ABC中，BC=2
，
，
.
（Ⅰ）求AB的值；w.w.（Ⅱ）求
的值.
17（本小題滿分12分）
設等差數列
滿足
，
。
（Ⅰ）求的通項公式；
（Ⅱ）求的前
項和
及使得最大的序號的值。
（本小題滿分12分）
已知斜率為1的直線1與雙曲線C：
相交于B、D兩點，且BD的中點為M（1.3）
（Ⅰ）（Ⅰ）求C的離心率；
（Ⅱ）（Ⅱ）設C的右頂點為A，右焦點為F，|DF|·|BF|=17證明：過A、B、D三點的圓與x軸相切。
（本小題滿分12分）
已知斜率為1的直線1與雙曲線C：
相交于B、D兩點，且BD的中點為M（1.3）
（Ⅰ）（Ⅰ）求C的離心率；
（Ⅱ）（Ⅱ）設C的右頂點為A，右焦點為F，|DF|·|BF|=17證明：過A、B、D三點的圓與x軸相切。
（本小題滿分12分）某港口海水的深度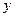
（米）是時間
（時）（
）的函數，記為：
已知某日海水深度的數據如下：
| （時） | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
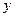| （米） | 10．0 | 13．0 | 9．9 | 7．0 | 10．0 | 13．0 | 10．1 | 7．0 | 10．0 |
的曲線可近似地看成函數
的圖象
（1）試根據以上數據，求出函數
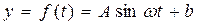的振幅A、最小正周期T和表達式；（2）一般情況下，船舶航行時，船底離海底的距離為
米或米以上時認為是安全的（船舶停靠時，船底只需不碰海底即可）。某船吃水深度（船底離水面的距離）為
米，如果該船希望在同一天內安全進出港，請問，它至多能在港內停留多長時間（忽略進出港所需時間）？一、1 B 2 D 3 A 4 D 5 C 6 B
7 A 8 A 9 C 10 D 11 C 12 B
二、13、3 14、
15、-160 16、 
三、17、解: (1)
……… 3分
的最小正周期為
…………………
5分
(2) 
, ………………… 7分
…………………
10分
………………… 11分
當
時,函數的最大值為1,最小值
……… 12分
18.解：(1)P1=
；
……… 6分
（2）方法一：P2=
方法二：P2=
方法三：P2=1-
……… 12分
19、解法一：
（Ⅰ）連結
C交BC
于O，則O是B 
C的中點，連結DO。
∵在△A
C中，O、D均為中點，
∴A∥DO…………………………2分
∵A
平面B
D，DO
平面BD，
∴A∥平面BD。…………………4分
（Ⅱ）設正三棱柱底面邊長為2，則DC = 1。
∵∠DC = 60°，∴C= 
。
作DE⊥BC于E。
∵平面BC⊥平面ABC，
∴DE⊥平面BC
作EF⊥B于F，連結DF，則 DF⊥B
∴∠DFE是二面角D-B-C的平面角………………8分
在Rt△DEC中，DE=
在Rt△BFE中，EF =
BE?sin
∴在Rt△DEF中，tan∠DFE = 
∴二面角D－B－C的大小為arctan
………………12分
解法二：以AC的中D為原點建立坐標系，如圖，
設| AD | = 1∵∠DC =60°∴| C|
= 。
則A（1，0，0），B（0，，0），C（-1，0，0），
（1，0），
，
（Ⅰ）連結C交B
于O是C的中點，連結DO，則
O
. 
=
∵A平面BD，
∴A∥平面BD.………………………………………………4分
（Ⅱ）
=（-1，0，），
設平面BD的法向量為n = （ x , y , z ），則
即
則有
= 0令z = 1
則n = （，0，1）
…………………………………8分
設平面BC的法向量為m = ( x′
,y′，z′)
令y = -1，解得m = （
…………１２分
)=
a+b=0, f′(1)=3+2a+b=0,得
，b=－2，………… ３分
+c為極大值，
的兩個根為
，
，
時，
，所以
；
時，
，
，所以
；
時，
，
，所以
時；
時，
，
，所以
．
…………
4分
． ………… 8分
=
…………
12分
的軌跡是以點
為焦點、直線
為其相應準線,
，
，∴點
,且
則
3
,
為橢圓的對稱中心
,設直線
的方程為
,代入
,
………… 6分
,
,
,
(舍)
…………8分
,由
知,
的斜率為
時,
;
時,
,
時取“=”）或
時取“=”），
………… 12分
………… 14分