
題目列表(包括答案和解析)
試求曲線![]() 在矩陣MN變換下的函數(shù)解析式,其中M =
在矩陣MN變換下的函數(shù)解析式,其中M =![]() ,N =
,N =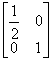 .
.
|
|
試求曲線y=sinx在矩陣MN變換下的函數(shù)解析式,其中M=![]() ,N=
,N=![]() .
.
 ,N=
,N=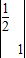 .
. ,N=
,N=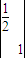 .
.A.必做題部分
一、填空題:(本大題共14小題,每小題5分,共70分.)
1.中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image263.gif) 2.
2.中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image265.gif) 3.共線 4.20 5.
3.共線 4.20 5.中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image267.gif) 6.
6.中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image269.gif) 7.
7.中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image271.gif) 8.2,5,10 9.16.4 10.1 11.7 12.
8.2,5,10 9.16.4 10.1 11.7 12.中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image273.gif) 13.2 14.
13.2 14.中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image275.gif)
二、解答題:
15.解:(1)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image277.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image279.gif)
(2)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image281.gif)
余弦定理中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image283.gif) 可得
可得中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image285.gif)
又∵中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image287.gif)
∴中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image289.gif)
16.證明中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image113.gif) (1)∵PA⊥底面ABCD,∴AD是PD在平面ABCD內(nèi)的射影,
(1)∵PA⊥底面ABCD,∴AD是PD在平面ABCD內(nèi)的射影,
(2)取CD中點G,連EG、FG,
∵E、F分別是AB、PC的中點,∴EG∥AD,F(xiàn)G∥PD
∴平面EFG∥平面PAD,故EF∥平面PAD
(3)解中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image113.gif) 當(dāng)平面PCD與平面ABCD成45°角時,直線EF⊥面PCD
當(dāng)平面PCD與平面ABCD成45°角時,直線EF⊥面PCD
證明中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image113.gif) G為CD中點,則EG⊥CD,由(1)知FG⊥CD,故∠EGF為平面PCD與平面ABCD所成二面角的平面角
G為CD中點,則EG⊥CD,由(1)知FG⊥CD,故∠EGF為平面PCD與平面ABCD所成二面角的平面角中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image109.gif) 即∠EGF=45°,從而得∠ADP=45°,AD=AP
即∠EGF=45°,從而得∠ADP=45°,AD=AP
由Rt△PAE≌Rt△CBE,得PE=CE
又F是PC的中點,∴EF⊥PC,由CD⊥EG,CD⊥FG,得CD⊥平面EFG,CD⊥EF即EF⊥CD,故EF⊥平面PCD中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image109.gif)
17.解:(1)依題意,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image128.gif) 到
到中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image123.gif) 距離等于
距離等于中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image128.gif) 到直線
到直線中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image296.gif) 的距離,曲線
的距離,曲線中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image130.gif) 是以原點為頂點,
是以原點為頂點,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image123.gif) 為焦點的拋物線
為焦點的拋物線
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image300.gif) 曲線
曲線中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image130.gif) 方程是
方程是中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image302.gif)
(2)設(shè)圓心中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image304.gif) ,因為圓
,因為圓中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image132.gif) 過
過中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image134.gif)
故設(shè)圓的方程中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image308.gif)
令中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image310.gif) 得:
得:中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image312.gif)
設(shè)圓與中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image056.gif) 軸的兩交點為
軸的兩交點為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image315.gif) ,則
,則中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image317.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image319.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image304.gif) 在拋物線
在拋物線中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image302.gif) 上,
上,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image323.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image325.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image327.gif)
所以,當(dāng)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image132.gif) 運動時,弦長
運動時,弦長中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image140.gif) 為定值2
為定值2
18.解(1)設(shè)日銷售量為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image331.gif)
則日利潤中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image333.gif)
(2)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image335.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image337.jpg) ①當(dāng)2≤a≤4時,33≤a+31≤35,當(dāng)35 <x<41時,
①當(dāng)2≤a≤4時,33≤a+31≤35,當(dāng)35 <x<41時,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image339.gif)
∴當(dāng)x=35時,L(x)取最大值為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image341.gif)
②當(dāng)4<a≤5時,35≤a+31≤36,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image343.gif)
易知當(dāng)x=a+31時,L(x)取最大值為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image345.gif) 綜合上得
綜合上得中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image347.gif)
19.解(1)據(jù)題意: 中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image349.gif)
可行域如圖(暫缺)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image148.gif) 的幾何意義是定點
的幾何意義是定點中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image351.gif) 到區(qū)域內(nèi)的點
到區(qū)域內(nèi)的點中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image353.gif) 連線的斜率
連線的斜率中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image153.gif) ,
,
又中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image356.gif)
故中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image148.gif) 的取值范圍為
的取值范圍為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image358.gif)
(2)當(dāng)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image070.gif) 有零點時,
有零點時,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image360.gif) ,滿足條件為
,滿足條件為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image362.gif)
由拋物線的下方與中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image364.gif) 圍成的區(qū)域面積
圍成的區(qū)域面積
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image366.gif)
由直線中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image368.gif) 圍成的區(qū)域面積
圍成的區(qū)域面積中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image370.gif)
故中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image070.gif) 有零點的概率
有零點的概率中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image372.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image374.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image070.gif) 無零點的概率為
無零點的概率為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image376.gif)
(3)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image164.gif) 是
是中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image160.gif) 函數(shù).
函數(shù).
證明: 中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image378.gif) 符合條件.
符合條件.
因為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image380.gif) ,
,
同理:中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image382.gif) ;
;
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image384.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image386.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image388.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image390.gif) .
.
所以, 中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image378.gif) 符合條件.
符合條件.
20.(1)解:由已知:對于中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image393.gif) ,總有
,總有中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image395.gif) ①成立
①成立
∴中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image397.gif) (n ≥ 2)②
(n ≥ 2)②
①--②得中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image399.gif)
∴中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image401.gif)
∵中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image403.gif) 均為正數(shù),∴
均為正數(shù),∴中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image405.gif) (n ≥ 2)
(n ≥ 2)
∴數(shù)列中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image166.gif) 是公差為1的等差數(shù)列
又n=1時,
是公差為1的等差數(shù)列
又n=1時,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image407.gif) ,
解得
,
解得中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image409.gif) =1
=1
∴中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image411.gif) .(
.(中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image393.gif) )
)
(2)證明:∵對任意實數(shù)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image182.gif) 和任意正整數(shù)n,總有
和任意正整數(shù)n,總有中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image180.gif) ≤
≤中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image414.gif) .……6分
.……6分
∴中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image416.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image418.gif)
(3)解:由已知 中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image420.gif) ,
,
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image422.gif)
易得 中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image424.gif)
猜想 n≥2 時,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image192.gif) 是遞減數(shù)列.
是遞減數(shù)列.
令中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image426.gif)
∵當(dāng)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image428.gif)
∴在中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image430.gif) 內(nèi)
內(nèi)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image432.gif) 為單調(diào)遞減函數(shù).
為單調(diào)遞減函數(shù).
由中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image434.gif) .
.
∴n≥2 時, 中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image436.gif) 是遞減數(shù)列.即
是遞減數(shù)列.即中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image192.gif) 是遞減數(shù)列.
是遞減數(shù)列.
又中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image438.gif) , ∴數(shù)列
, ∴數(shù)列中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image192.gif) 中的最大項為
中的最大項為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image440.gif) .
.
B.附加題部分
三、附加題部分:
21.(必做題)(本小題滿分12分)
解:(1)將中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image196.gif) 代入
代入中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image198.gif) 得
得中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image442.gif) ,
,
由△中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image444.gif) 可知
可知中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image446.gif) ,
,
另一方面,弦長AB中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image448.gif) ,解得
,解得中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image450.gif) ;
;
(2)當(dāng)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image450.gif) 時,直線為
時,直線為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image452.gif) ,要使得內(nèi)接△ABC面積最大,
,要使得內(nèi)接△ABC面積最大,
則只須使得中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image454.gif) ,
,
即中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image456.gif) ,即
,即中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image130.gif) 位于(4,4)點處.
位于(4,4)點處.
22.(必做題)(本小題滿分12分)
解:(1)分別記甲、乙、丙三個同學(xué)筆試合格為事件中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image459.gif) 、
、中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image461.gif) 、
、中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image463.gif) ;
;
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image222.gif) 表示事件“恰有一人通過筆試”
表示事件“恰有一人通過筆試”
則中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image466.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image468.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image470.gif)
(2)解法一:因為甲、乙、丙三個同學(xué)經(jīng)過兩次考試后合格的概率均為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image472.gif) ,
,
所以中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image474.gif) ,故
,故中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image476.gif) .
.
解法二:分別記甲、乙、丙三個同學(xué)經(jīng)過兩次考試后合格為事件中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image478.gif) ,
,
則中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image480.gif)
所以中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image482.gif) ,
,
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image484.gif) ,
,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image486.gif) .
.
于是,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image488.gif) .
.
23.(選做題)(本小題滿分8分)
證明:(1)過D點作DG∥BC,并交AF于G點,
∵E是BD的中點,∴BE=DE,
又∵∠EBF=∠EDG,∠BEF=∠DEG,
∴△BEF≌△DEG,則BF=DG,
∴BF:FC=DG:FC,
又∵D是AC的中點,則DG:FC=1:2,
則BF:FC=1:2;
(2)若△BEF以BF為底,△BDC以BC為底,
則由(1)知BF:BC=1:3,
又由BE:BD=1:2可知中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image490.gif) :
:中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image492.gif) =1:2,其中
=1:2,其中中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image490.gif) 、
、中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image492.gif) 分別為△BEF和△BDC的高,
分別為△BEF和△BDC的高,
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image496.gif) 則
則中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image498.gif) ,則
,則中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image244.gif) =1:5.
=1:5.
24.(選做題)(本小題滿分8分)
解:(1)消去參數(shù)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image250.gif) ,得直線
,得直線中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image246.gif) 的普通方程為
的普通方程為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image452.gif) ;-----------------------2分
;-----------------------2分
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image501.gif) 即
即中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image503.gif) ,
,
兩邊同乘以中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image505.gif) 得
得中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image507.gif) ,
,
消去參數(shù)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image509.gif) ,得⊙
,得⊙中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image130.gif) 的直角坐標(biāo)方程為:
的直角坐標(biāo)方程為:
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image511.gif)
(2)圓心中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image130.gif) 到直線
到直線中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image246.gif) 的距離
的距離中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image514.gif) ,
,
所以直線中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image246.gif) 和⊙
和⊙中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image130.gif) 相交.
相交.
25.(選做題)(本小題滿分8分)
解:MN = 中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image257.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image259.gif) =
=中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image516.gif) ,
,
即在矩陣MN變換下中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image518.gif) ,
,
則中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image520.gif) ,
,
即曲線中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image255.gif) 在矩陣MN變換下的函數(shù)解析式為
在矩陣MN變換下的函數(shù)解析式為中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image522.gif) .
.
26.(選做題)(本小題滿分8分)
證明:(1)當(dāng)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image524.gif) 時,左邊=
時,左邊=中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image526.gif) ,
,中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image374.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image524.gif) 時成立
時成立
(2)假設(shè)當(dāng)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image530.gif) 時成立,即
時成立,即中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image532.gif)
那么當(dāng)中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image534.gif) 時,左邊
時,左邊中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image536.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image538.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image540.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image374.gif)
中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image534.gif) 時也成立
時也成立
根據(jù)(1)(2)可得不等式對所有的中學(xué)09屆高三3月份月考數(shù)學(xué)試題2009-03-30.files/image544.gif) 都成立
都成立
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com