
題目列表(包括答案和解析)
已知數列![]() 滿足
滿足![]()
(1)求數列![]() 的通項公式;
的通項公式;
(2)設b![]() =
=![]() (n∈N
(n∈N![]() ,n≥2), b
,n≥2), b![]() ,
,
求證:b1+b2……+bn< 3;
(3)設點M![]() (n,b
(n,b![]() )((n∈N
)((n∈N![]() ,n>2)在這些點中是否存在兩個不同的點同時在函數
,n>2)在這些點中是否存在兩個不同的點同時在函數
y =![]() (k>0)的圖象上,如果存在,求出點的坐標,若不存在,請說明理由.
(k>0)的圖象上,如果存在,求出點的坐標,若不存在,請說明理由.
(1)求數列{bn}的通項公式;
(2)設cn=bn+8n+3,數列{dn}滿足d1=c1,dn+1=cdn(n∈N*).求數列{dn}的前n項和Dn;
(3)設g(x)是定義在正整數集上的函數,對于任意的正整數x1,x2恒有g(x1x2)=x1g(x2)+x2g(x1)成立,且g(2)=a(a為常數,a≠0),試判斷數列{ }是否為等差數列,并說明理由.
}是否為等差數列,并說明理由.
| 1 |
| n+a1 |
| 1 |
| n+a2 |
| 1 |
| n+a3 |
| 1 |
| n+an |
| 1 |
| 2 |
| 1 |
| 2 |
已知數列{an}中,a1=1,且點P(an,an+1)在直線x-y+1=0上。
(1)求數列{an}的通項公式;
(2)若函數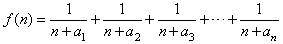 (n∈N,且n≥2),求函數f(n)的最小值;
(n∈N,且n≥2),求函數f(n)的最小值;
(3)設bn=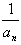 ,Sn表示數列{bn}的前n項和。試問:是否存在關于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)·g(n)對于一切不小于2的自然數n恒成立? 若存在,寫出g(n)的解析式,并加以證明;若不存在,試說明理由。
,Sn表示數列{bn}的前n項和。試問:是否存在關于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)·g(n)對于一切不小于2的自然數n恒成立? 若存在,寫出g(n)的解析式,并加以證明;若不存在,試說明理由。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com