
題目列表(包括答案和解析)
函數 .
.
(1)當 時,對任意
時,對任意 R,存在
R,存在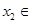 R,使
R,使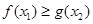 ,求實數
,求實數 的取值范圍;
的取值范圍;
(2)若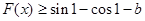 對任意
對任意 恒成立,求實數
恒成立,求實數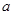 的取值范圍.
的取值范圍.
函數 .
.
(1)當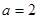 時,對任意
時,對任意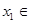 R,存在
R,存在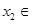 R,使
R,使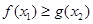 ,求實數
,求實數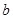 的取值范圍;
的取值范圍;
(2)若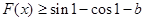 對任意
對任意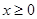 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
已知函數![]()
(1)若![]() 對任意的
對任意的![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,設函數
時,設函數![]() ,若
,若![]() ,求證
,求證![]()
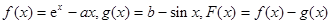 .
.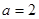 時,對任意
時,對任意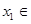 R,存在
R,存在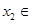 R,使
R,使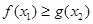 ,求實數
,求實數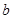 的取值范圍;
的取值范圍;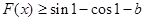 對任意
對任意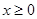 恒成立,求實數
恒成立,求實數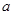 的取值范圍.
的取值范圍.已知函數
(Ⅰ)當 時,求
時,求 的單調區間;
的單調區間;
(Ⅱ)若對任意 ,
,  恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
(一)
【解題思路】:設f(x)的二次項系數為m,其圖象上兩點為(1-x,有詳細的答案或解析.files/image196.gif) )、B(1+x,
)、B(1+x,有詳細的答案或解析.files/image198.gif) )因為
)因為有詳細的答案或解析.files/image200.gif) ,
,有詳細的答案或解析.files/image006.gif) ,所以
,所以有詳細的答案或解析.files/image203.gif) ,由x的任意性得f(x)的圖象關于直線x=1對稱, ………………………………………………………………(2分)
,由x的任意性得f(x)的圖象關于直線x=1對稱, ………………………………………………………………(2分)
∵ 有詳細的答案或解析.files/image205.gif) ,
,有詳細的答案或解析.files/image207.gif) ,
,有詳細的答案或解析.files/image209.gif) ,
,
有詳細的答案或解析.files/image211.gif) ,
,有詳細的答案或解析.files/image213.gif) ,
,有詳細的答案或解析.files/image215.gif)
有詳細的答案或解析.files/image217.gif) ,………………………………(4分)
,………………………………(4分)
∴ 當有詳細的答案或解析.files/image219.gif) 時,∵f(x)在x≥1內是增函數,
時,∵f(x)在x≥1內是增函數,
有詳細的答案或解析.files/image221.gif)
有詳細的答案或解析.files/image223.gif)
有詳細的答案或解析.files/image225.gif)
有詳細的答案或解析.files/image227.gif)
有詳細的答案或解析.files/image229.gif)
有詳細的答案或解析.files/image231.gif) ,
,有詳細的答案或解析.files/image233.gif) .
.
∵ 有詳細的答案或解析.files/image235.gif) , ∴
, ∴ 有詳細的答案或解析.files/image237.gif) .………………………………………………(8分)
.………………………………………………(8分)
當有詳細的答案或解析.files/image239.gif) 時,∵f(x)在x≥1內是減函數.
時,∵f(x)在x≥1內是減函數.
同理可得有詳細的答案或解析.files/image241.gif) 或
或有詳細的答案或解析.files/image243.gif) ,
,有詳細的答案或解析.files/image233.gif) .………………………………………(11分)
.………………………………………(11分)
綜上:有詳細的答案或解析.files/image245.gif) 的解集是當
的解集是當有詳細的答案或解析.files/image219.gif) 時,為
時,為有詳細的答案或解析.files/image248.gif)
當有詳細的答案或解析.files/image239.gif) 時,為
時,為有詳細的答案或解析.files/image251.gif) ,或
,或有詳細的答案或解析.files/image253.gif) .…………………………(12分)
.…………………………(12分)
【試題評析】:本小題主要考查最簡單三角不等式的解法等基本知識,涉及到分類討論、二次函數的對稱性、向量的數量積、函數的單調性等基本知識和方法的綜合運用,考查運算能力及邏輯思維能力。
18.(理)【解題思路】:(1)設甲隊在第五場比賽后獲得冠軍為事件M,則第五場比賽甲隊獲勝,前四場比賽甲隊獲勝三場,
依題意得有詳細的答案或解析.files/image255.gif) .……………………………(6分)
.……………………………(6分)
(2)設甲隊獲得冠軍為事件E,則E包含第四、第五、第六、第七場獲得冠軍四種情況,且它們彼此互斥.
∴ 有詳細的答案或解析.files/image257.gif) .
.
………………………………………………………………(12分)
【試題評析】:考查互斥事件有一個發生的概率,相互獨立事件同時發生的概率,n次獨立重復實驗恰好k次發生的概率。考查邏輯思維能力,要求考生具有較強的辨別雷同信息的能力。
19.【解題思路】:解法一:(1)取PC中點M,連結ME、MF,則MF∥CD,MF=有詳細的答案或解析.files/image012.gif) CD,又AE∥CD,AE=
CD,又AE∥CD,AE=有詳細的答案或解析.files/image012.gif) CD,∴AE∥MF,且AE=MF,∴四邊形AFME是平行四邊形,∴AF∥EM,∵AF
CD,∴AE∥MF,且AE=MF,∴四邊形AFME是平行四邊形,∴AF∥EM,∵AF有詳細的答案或解析.files/image261.gif) 平面PCE,∴AF∥平面PCE.
…………………………………(4分)
平面PCE,∴AF∥平面PCE.
…………………………………(4分)
(2)∵PA⊥平面ABCD,CD⊥AD. ∴CD⊥PD,∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°, ………………………………………………………………(6分)
∴△PAD是等腰直角三角形,∴AF⊥PD,又AF⊥CD,∴AF⊥平面PCD,而EM∥AF,∴EM⊥平面PCD.
又EM有詳細的答案或解析.files/image263.gif) 平面PEC,∴面PEC⊥面PCD.
在平面PCD內過F作FH⊥PC于H,則FH就是點F到平面PCE的距離.
…………………………………(10分)
平面PEC,∴面PEC⊥面PCD.
在平面PCD內過F作FH⊥PC于H,則FH就是點F到平面PCE的距離.
…………………………………(10分)
由已知,PD=有詳細的答案或解析.files/image265.gif) ,PF=
,PF=有詳細的答案或解析.files/image267.gif) ,PC=
,PC=有詳細的答案或解析.files/image269.gif) ,△PFH∽△PCD,∴
,△PFH∽△PCD,∴有詳細的答案或解析.files/image271.gif) ,
,
∴FH=有詳細的答案或解析.files/image273.gif) .
………………………………………………………………(12分)
.
………………………………………………………………(12分)
解法二:(1)取PC中點M,連結EM,有詳細的答案或解析.files/image275.gif)
有詳細的答案或解析.files/image012.gif)
有詳細的答案或解析.files/image278.gif)
有詳細的答案或解析.files/image280.gif)
有詳細的答案或解析.files/image282.gif) =
=有詳細的答案或解析.files/image284.gif) +
+有詳細的答案或解析.files/image012.gif)
有詳細的答案或解析.files/image287.gif) =
=有詳細的答案或解析.files/image289.gif) ,∴AF∥EM,又EM
,∴AF∥EM,又EM有詳細的答案或解析.files/image263.gif) 平面PEC,AF
平面PEC,AF有詳細的答案或解析.files/image261.gif) 平面PEC,∴AF∥平面PEC.
………………………………………………(4分)
平面PEC,∴AF∥平面PEC.
………………………………………………(4分)
有詳細的答案或解析.files/image293.jpg) (2)以A為坐標原點,分別以
(2)以A為坐標原點,分別以有詳細的答案或解析.files/image295.gif) 所在直線為x、y、z
所在直線為x、y、z
軸建立坐標系. ∵PA⊥平面ABCD,CD⊥AD,∴CD⊥PD,
∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°. ……(6分)
∴A(0, 0, 0), P(0, 0,
2), D(0, 2, 0), F(0, 1, 1), E有詳細的答案或解析.files/image297.gif) ,
C(3, 2, 0),設平面PCE的法向量為
,
C(3, 2, 0),設平面PCE的法向量為有詳細的答案或解析.files/image299.gif) =(x, y, z),則
=(x, y, z),則有詳細的答案或解析.files/image299.gif) ⊥
⊥有詳細的答案或解析.files/image302.gif) ,
,有詳細的答案或解析.files/image299.gif) ⊥
⊥有詳細的答案或解析.files/image304.gif) ,而
,而有詳細的答案或解析.files/image302.gif) =(-
=(-有詳細的答案或解析.files/image307.gif) ,0,2),
,0,2),
有詳細的答案或解析.files/image304.gif) =(
=(有詳細的答案或解析.files/image307.gif) ,2,0),∴-
,2,0),∴-有詳細的答案或解析.files/image307.gif) x+2z=0,且
x+2z=0,且有詳細的答案或解析.files/image307.gif) x+2y=0,解得y=-
x+2y=0,解得y=-有詳細的答案或解析.files/image310.gif) x,z=
x,z=有詳細的答案或解析.files/image310.gif) x.
取x=4
x.
取x=4
得有詳細的答案或解析.files/image299.gif) =(4, -3, 3),………………………………………………………………(10分)
=(4, -3, 3),………………………………………………………………(10分)
又有詳細的答案或解析.files/image312.gif) =(0,1,-1),
=(0,1,-1),
故點F到平面PCE的距離為d=有詳細的答案或解析.files/image314.gif) .…………(12分)
.…………(12分)
【試題評析】:本小題主要考查直線與平面的位置關系等基本知識,是否利用空間向量供考生選擇。考查空間想象能力、邏輯推理能力和運算能力有詳細的答案或解析.files/image316.gif)
(二)
17. 解:(1) 設有詳細的答案或解析.files/image318.gif) ,則
,則有詳細的答案或解析.files/image320.gif) …………………1分
…………………1分
有詳細的答案或解析.files/image322.gif) …………………2分
…………………2分
又有詳細的答案或解析.files/image002.gif) 是奇函數,所以
是奇函數,所以有詳細的答案或解析.files/image325.gif) …………………3分
…………………3分
有詳細的答案或解析.files/image327.gif)
有詳細的答案或解析.files/image329.gif) =
=有詳細的答案或解析.files/image331.gif) ……4分
……4分
………………5分
有詳細的答案或解析.files/image002.gif) 是[-1,1]上增函數………………6分
是[-1,1]上增函數………………6分
(2)有詳細的答案或解析.files/image333.gif) 是[-1,1]上增函數,由已知得:
是[-1,1]上增函數,由已知得:有詳細的答案或解析.files/image335.gif) …………7分
…………7分
等價于有詳細的答案或解析.files/image337.gif) …………10分
…………10分
解得:有詳細的答案或解析.files/image339.gif) ,所以
,所以有詳細的答案或解析.files/image341.gif) …………12分
…………12分
有詳細的答案或解析.files/image343.gif)
有詳細的答案或解析.files/image345.gif) 二次函數
二次函數有詳細的答案或解析.files/image347.gif) 在
在有詳細的答案或解析.files/image349.gif) 上遞減………………………12分
上遞減………………………12分
故有詳細的答案或解析.files/image351.gif) 時,
時,有詳細的答案或解析.files/image353.gif)
有詳細的答案或解析.files/image355.gif) ……………………13分
……………………13分
有詳細的答案或解析.files/image357.gif) ,
,有詳細的答案或解析.files/image359.gif) …………………………14分
…………………………14分
(三)
16.解: 由題意,得有詳細的答案或解析.files/image361.gif) 為銳角,
為銳角,有詳細的答案或解析.files/image363.gif) , 3分
, 3分
有詳細的答案或解析.files/image365.gif) , 6分
, 6分
由正弦定理得 有詳細的答案或解析.files/image367.gif) , 9分
, 9分
有詳細的答案或解析.files/image345.gif)
有詳細的答案或解析.files/image370.gif) . 12分
. 12分
17.(本題滿分12分)
有紅藍兩粒質地均勻的正方體形狀骰子,紅色骰子有兩個面是8,四個面是2,藍色骰子有三個面是7,三個面是1,兩人各取一只骰子分別隨機擲一次,所得點數較大者獲勝.
(1)分別求出兩只骰子投擲所得點數的分布列及期望;
(2)求投擲藍色骰子者獲勝的概率是多少?
17.解:(1)設紅色骰子投擲所得點數為有詳細的答案或解析.files/image372.gif) ,其分布如下:
,其分布如下:
有詳細的答案或解析.files/image374.gif)
8
2
P
有詳細的答案或解析.files/image092.gif)
|