
題目列表(包括答案和解析)
| cn+1 |
| cn |
| 5 |
| 4 |
| 1 |
| 100 |
已知數(shù)列{an}中,a1=,點(diǎn)(n,2an+1-an)(n∈N*)在直線y=x上。
(I)計(jì)算a2,a3,a4的值;
(II)令bn=an+1-an-1,求證:數(shù)列{bn}是等比數(shù)列;
(III)設(shè)Sn、Tn分別為數(shù)列{an}、{bn}的前n項(xiàng)和,是否存在實(shí)數(shù)λ,使得數(shù)列{}為等差數(shù)列?若存在,試求出λ的值;若不存在,請(qǐng)說(shuō)明理由。
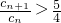 的正整數(shù)n的個(gè)數(shù);
的正整數(shù)n的個(gè)數(shù);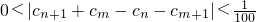 成立.
成立.已知數(shù)列![]() 的首項(xiàng)
的首項(xiàng)![]() 前
前![]() 項(xiàng)和為
項(xiàng)和為![]() ,且
,且![]()
(I)證明:數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(II)令![]() ,求函數(shù)
,求函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的導(dǎo)數(shù)
處的導(dǎo)數(shù)![]() ,并比較
,并比較![]() 與
與![]() 的大小.
的大小.
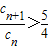 的正整數(shù)n的個(gè)數(shù);
的正整數(shù)n的個(gè)數(shù);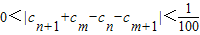 成立.
成立.一、選擇題(每小題5分,共計(jì)60分)
ABADD CACAC AB
二、填空題(每小題4分,共計(jì)16分)
(13)4;(14)學(xué)理科.files/image179.gif) ;(15)
;(15)學(xué)理科.files/image252.gif) ;(16)①④.
;(16)①④.
三、解答題:
17.解:(本小題滿分12分)
(Ⅰ) 由題意學(xué)理科.files/image254.gif)
學(xué)理科.files/image256.gif)
學(xué)理科.files/image258.gif)
學(xué)理科.files/image260.gif)
由題意,函數(shù)周期為3學(xué)理科.files/image262.gif) ,又
,又學(xué)理科.files/image164.gif) >0,
>0,學(xué)理科.files/image265.gif) ;
;
(Ⅱ) 由(Ⅰ)知學(xué)理科.files/image267.gif)
學(xué)理科.files/image269.gif)
學(xué)理科.files/image271.gif)
又x學(xué)理科.files/image273.gif) ,
,學(xué)理科.files/image275.gif)
學(xué)理科.files/image031.gif) 的減區(qū)間是
的減區(qū)間是學(xué)理科.files/image278.gif) .
.
(18) (本小題滿分12分)
解:(1)隨機(jī)變量學(xué)理科.files/image181.gif) 的所有可能取值為
的所有可能取值為學(xué)理科.files/image280.gif)
學(xué)理科.files/image282.gif)
學(xué)理科.files/image284.gif)
學(xué)理科.files/image286.gif)
學(xué)理科.files/image288.gif)
學(xué)理科.files/image290.gif)
學(xué)理科.files/image292.gif)
所以隨機(jī)變量學(xué)理科.files/image181.gif) 的分布列為
的分布列為
學(xué)理科.files/image181.gif)
0
1
2
3
4
5
學(xué)理科.files/image098.gif)
學(xué)理科.files/image295.gif)
學(xué)理科.files/image297.gif)
學(xué)理科.files/image297.gif)
學(xué)理科.files/image300.gif)
學(xué)理科.files/image302.gif)
學(xué)理科.files/image304.gif)
(2)∵隨機(jī)變量學(xué)理科.files/image306.gif)
∴學(xué)理科.files/image308.gif)
19. (本小題滿分12分)
解:(Ⅰ)學(xué)理科.files/image310.gif) ∵ 底面ABCD是正方形,
∵ 底面ABCD是正方形,
∴AB⊥BC,
又平面PBC⊥底面ABCD
平面PBC ∩ 平面ABCD=BC
∴AB ⊥平面PBC
又PC學(xué)理科.files/image312.gif) 平面PBC
平面PBC
∴AB ⊥CP ………………3分
(Ⅱ)解法一:體積法.由題意,面學(xué)理科.files/image314.gif) 面
面學(xué)理科.files/image316.gif) ,
,
取學(xué)理科.files/image318.gif) 中點(diǎn)
中點(diǎn)學(xué)理科.files/image320.gif) ,則
,則學(xué)理科.files/image322.gif)
學(xué)理科.files/image324.gif) 面
面學(xué)理科.files/image316.gif) .
.
再取學(xué)理科.files/image326.gif) 中點(diǎn)
中點(diǎn)學(xué)理科.files/image093.gif) ,則
,則學(xué)理科.files/image329.gif) ………………5分
………………5分
設(shè)點(diǎn)學(xué)理科.files/image091.gif) 到平面
到平面學(xué)理科.files/image189.gif) 的距離為
的距離為學(xué)理科.files/image331.gif) ,則由
,則由學(xué)理科.files/image333.gif)
學(xué)理科.files/image335.gif)
學(xué)理科.files/image337.gif)
學(xué)理科.files/image339.gif)
學(xué)理科.files/image341.gif) .
………………7分
.
………………7分
學(xué)理科.files/image342.gif) 解法二:
解法二:學(xué)理科.files/image344.gif) 面
面學(xué)理科.files/image189.gif)
取學(xué)理科.files/image318.gif) 中點(diǎn)
中點(diǎn)學(xué)理科.files/image320.gif) ,再取
,再取學(xué)理科.files/image326.gif) 中點(diǎn)
中點(diǎn)學(xué)理科.files/image093.gif)
學(xué)理科.files/image346.gif)
學(xué)理科.files/image348.gif) ,
,學(xué)理科.files/image350.gif)
學(xué)理科.files/image335.gif)
學(xué)理科.files/image353.gif)
過(guò)點(diǎn)學(xué)理科.files/image320.gif) 作
作學(xué)理科.files/image356.gif) ,則
,則學(xué)理科.files/image358.gif)
在學(xué)理科.files/image360.gif) 中,
中,
由學(xué)理科.files/image362.gif)
∴點(diǎn)學(xué)理科.files/image091.gif) 到平面
到平面學(xué)理科.files/image189.gif) 的距離為
的距離為學(xué)理科.files/image016.gif) 。 ………………7分
。 ………………7分
解法三:向量法(略)
(Ⅲ)學(xué)理科.files/image365.gif)
學(xué)理科.files/image344.gif) 面
面學(xué)理科.files/image189.gif)
學(xué)理科.files/image368.gif)
學(xué)理科.files/image370.gif)
學(xué)理科.files/image372.gif) 就是二面角
就是二面角學(xué)理科.files/image196.gif) 的平面角.
的平面角.
學(xué)理科.files/image374.gif)
學(xué)理科.files/image376.gif)
∴二面角學(xué)理科.files/image196.gif) 的大小為45°. ………………12分
的大小為45°. ………………12分
方法二:向量法(略).
(20)(本小題滿分12分)
解:(Ⅰ)方法一:∵學(xué)理科.files/image378.gif) ,
,
∴學(xué)理科.files/image380.gif) .
.
設(shè)直線學(xué)理科.files/image382.gif) ,
,
并設(shè)l與g(x)=x2相切于點(diǎn)M(學(xué)理科.files/image384.gif) )
)
∵學(xué)理科.files/image310.gif)
學(xué)理科.files/image386.gif) ∴2
∴2學(xué)理科.files/image388.gif)
∴學(xué)理科.files/image390.gif)
代入直線l方程解得p=1或p=3.
方法二:
將直線方程l代入 學(xué)理科.files/image392.gif) 得
得
學(xué)理科.files/image394.gif)
∴學(xué)理科.files/image396.gif)
解得p=1或p=3 .
(Ⅱ)∵學(xué)理科.files/image398.gif) ,
,
①要使學(xué)理科.files/image031.gif) 為單調(diào)增函數(shù),須
為單調(diào)增函數(shù),須學(xué)理科.files/image401.gif) 在
在學(xué)理科.files/image403.gif) 恒成立,
恒成立,
即學(xué)理科.files/image405.gif) 在
在學(xué)理科.files/image403.gif) 恒成立,即
恒成立,即學(xué)理科.files/image407.gif) 在
在學(xué)理科.files/image403.gif) 恒成立,
恒成立,
又學(xué)理科.files/image409.gif) ,所以當(dāng)
,所以當(dāng)學(xué)理科.files/image411.gif) 時(shí),
時(shí),學(xué)理科.files/image031.gif) 在
在學(xué)理科.files/image403.gif) 為單調(diào)增函數(shù); …………6分
為單調(diào)增函數(shù); …………6分
②要使學(xué)理科.files/image031.gif) 為單調(diào)減函數(shù),須
為單調(diào)減函數(shù),須學(xué)理科.files/image414.gif) 在
在學(xué)理科.files/image403.gif) 恒成立,
恒成立,
即學(xué)理科.files/image416.gif) 在
在學(xué)理科.files/image403.gif) 恒成立,即
恒成立,即學(xué)理科.files/image418.gif) 在
在學(xué)理科.files/image403.gif) 恒成立,
恒成立,
又學(xué)理科.files/image420.gif) ,所以當(dāng)
,所以當(dāng)學(xué)理科.files/image422.gif) 時(shí),
時(shí),學(xué)理科.files/image031.gif) 在
在學(xué)理科.files/image403.gif) 為單調(diào)減函數(shù).
為單調(diào)減函數(shù).
綜上,若學(xué)理科.files/image031.gif) 在
在學(xué)理科.files/image403.gif) 為單調(diào)函數(shù),則
為單調(diào)函數(shù),則學(xué)理科.files/image424.gif) 的取值范圍為
的取值范圍為學(xué)理科.files/image411.gif) 或
或學(xué)理科.files/image422.gif) .………8分
.………8分
(21) (本小題滿分12分)
(1)∵直線學(xué)理科.files/image194.gif) 的方向向量為
的方向向量為學(xué)理科.files/image204.gif)
∴直線學(xué)理科.files/image194.gif) 的斜率為
的斜率為學(xué)理科.files/image426.gif) ,又∵直線
,又∵直線學(xué)理科.files/image194.gif) 過(guò)點(diǎn)
過(guò)點(diǎn)學(xué)理科.files/image207.gif)
∴直線學(xué)理科.files/image194.gif) 的方程為
的方程為學(xué)理科.files/image428.gif)
∵學(xué)理科.files/image430.gif) ,∴橢圓的焦點(diǎn)為直線
,∴橢圓的焦點(diǎn)為直線學(xué)理科.files/image194.gif) 與
與學(xué)理科.files/image119.gif) 軸的交點(diǎn)
軸的交點(diǎn)
∴橢圓的焦點(diǎn)為學(xué)理科.files/image433.gif)
∴學(xué)理科.files/image435.gif) ,又∵
,又∵學(xué)理科.files/image437.gif)
∴學(xué)理科.files/image439.gif) ,∴
,∴學(xué)理科.files/image441.gif)
∴橢圓方程為學(xué)理科.files/image443.gif)
(2)設(shè)直線MN的方程為學(xué)理科.files/image445.gif)
由學(xué)理科.files/image447.gif) ,
,學(xué)理科.files/image310.gif) 得
得
學(xué)理科.files/image449.gif)
設(shè)學(xué)理科.files/image216.gif) 坐標(biāo)分別為
坐標(biāo)分別為學(xué)理科.files/image452.gif)
則學(xué)理科.files/image310.gif)
學(xué)理科.files/image454.gif) (1)
(1) 學(xué)理科.files/image456.gif) (2)
(2)
學(xué)理科.files/image458.gif) >0
>0
∴學(xué)理科.files/image310.gif)
學(xué)理科.files/image460.gif) ,
,
∵學(xué)理科.files/image462.gif) ,顯然
,顯然學(xué)理科.files/image464.gif) ,且
,且學(xué)理科.files/image466.gif)
∴學(xué)理科.files/image468.gif)
∴學(xué)理科.files/image470.gif)
代入(1) (2),得
學(xué)理科.files/image310.gif)
學(xué)理科.files/image472.gif)
∵學(xué)理科.files/image310.gif)
學(xué)理科.files/image460.gif) ,得
,得
學(xué)理科.files/image474.gif) ,即
,即
學(xué)理科.files/image476.gif)
解得學(xué)理科.files/image478.gif) 且
且學(xué)理科.files/image480.gif) .
.
(22) (本小題滿分14分)
(1) 解:過(guò)學(xué)理科.files/image226.gif) 的直線方程為
的直線方程為學(xué)理科.files/image482.gif)
聯(lián)立方程學(xué)理科.files/image484.gif) 消去
消去學(xué)理科.files/image036.gif) 得
得
學(xué)理科.files/image487.gif)
∴學(xué)理科.files/image489.gif)
即學(xué)理科.files/image491.gif)
(2)學(xué)理科.files/image493.gif)
∴學(xué)理科.files/image495.gif) 是等比數(shù)列
是等比數(shù)列
學(xué)理科.files/image497.gif) ,
,學(xué)理科.files/image499.gif) ;
;
(III)學(xué)理科.files/image310.gif) 由(II)知,
由(II)知,學(xué)理科.files/image501.gif) ,要使
,要使學(xué)理科.files/image503.gif) 恒成立由
恒成立由學(xué)理科.files/image505.gif)
學(xué)理科.files/image507.gif) =
=學(xué)理科.files/image509.gif) >0恒成立,
>0恒成立,
即(-1)nλ>-(學(xué)理科.files/image511.gif) )n-1恒成立.
)n-1恒成立.
?。當(dāng)n為奇數(shù)時(shí),即λ<(學(xué)理科.files/image511.gif) )n-1恒成立.
)n-1恒成立.
又(學(xué)理科.files/image511.gif) )n-1的最小值為1.∴λ<1. 10分
)n-1的最小值為1.∴λ<1. 10分
?。當(dāng)n為偶數(shù)時(shí),即λ>-(學(xué)理科.files/image511.gif) )n-1恒成立,
)n-1恒成立,
又-(學(xué)理科.files/image511.gif) )n-1的最大值為-
)n-1的最大值為-學(xué)理科.files/image511.gif) ,∴λ>-
,∴λ>-學(xué)理科.files/image511.gif) . 11分
. 11分
即-學(xué)理科.files/image511.gif) <λ<1,又λ≠0,λ為整數(shù),
<λ<1,又λ≠0,λ為整數(shù),
∴λ=-1,使得對(duì)任意n∈N*,都有學(xué)理科.files/image503.gif) .
.
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com