
題目列表(包括答案和解析)
若n為大于1的自然數(shù),求證:![]() .
.
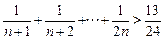 .
.若n為大于1的自然數(shù),求證:![]() +
+![]() +…+
+…+![]() >
>![]() 。
。
難點磁場
解:假設(shè)存在a、b、c使題設(shè)的等式成立,這時令n=1,2,3,有
于是,對n=1,2,3下面等式成立
記Sn=1?22+2?32+…+n(n+1)2
設(shè)n=k時上式成立,即Sk= (3k2+11k+10)
(3k2+11k+10)
那么Sk+1=Sk+(k+1)(k+2)2= (k+2)(3k+5)+(k+1)(k+2)2
(k+2)(3k+5)+(k+1)(k+2)2
也就是說,等式對n=k+1也成立.
綜上所述,當(dāng)a=3,b=11,c=10時,題設(shè)對一切自然數(shù)n均成立.
殲滅難點訓(xùn)練
一、1.解析:∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36
∴f(1),f(2),f(3)能被36整除,猜想f(n)能被36整除.
證明:n=1,2時,由上得證,設(shè)n=k(k≥2)時,
f(k)=(2k+7)?3k+9能被36整除,則n=k+1時,
f(k+1)-f(k)=(2k+9)?3k+1?-(2k+7)?3k
=(6k+27)?3k-(2k+7)?3k
=(4k+20)?3k=36(k+5)?3k-2?(k≥2)
∵f(1)不能被大于36的數(shù)整除,∴所求最大的m值等于36.
答案:C
2.解析:由題意知n≥3,∴應(yīng)驗證n=3.
答案:C
三、5.證明:(1)當(dāng)n=1時,42×1+1+31+2=91能被13整除
(2)假設(shè)當(dāng)n=k時,42k+1+3k+2能被13整除,則當(dāng)n=k+1時,
42(k+1)+1+3k+3=42k+1?42+3k+2?3-42k+1?3+42k+1?3
=42k+1?13+3?(42k+1+3k+2?)
∵42k+1?13能被13整除,42k+1+3k+2能被13整除
∴當(dāng)n=k+1時也成立.
由①②知,當(dāng)n∈N*時,42n+1+3n+2能被13整除.
7.(1)解:設(shè)數(shù)列{bn}的公差為d,由題意得 ,∴bn=3n-2
,∴bn=3n-2
(2)證明:由bn=3n-2知
Sn=loga(1+1)+loga(1+ )+…+loga(1+
)+…+loga(1+ )
)
而 logabn+1=loga
logabn+1=loga ,于是,比較Sn與
,于是,比較Sn與 logabn+1?的大小
logabn+1?的大小 比較(1+1)(1+
比較(1+1)(1+ )…(1+
)…(1+ )與
)與 的大小.
的大小.
①當(dāng)n=1時,已驗證(*)式成立.
②假設(shè)n=k(k≥1)時(*)式成立,即(1+1)(1+ )…(1+
)…(1+ )>
)>
由①②知,(*)式對任意正整數(shù)n都成立.
于是,當(dāng)a>1時,Sn> logabn+1?,當(dāng) 0<a<1時,Sn<
logabn+1?,當(dāng) 0<a<1時,Sn< logabn+1?
logabn+1?
8.解:∵a1?a2=-q,a1=2,a2≠0,
∵an?an+1=-qn,an+1?an+2=-qn+1?
于是,a1=2,a3=2?q,a5=2?qn…猜想:a2n+1=- qn(n=1,2,3,…)
qn(n=1,2,3,…)
下證:(1)當(dāng)n=1,2時猜想成立
(2)設(shè)n=2k-1時,a2k-1=2?qk-1則n=2k+1時,由于a2k+1=q?a2k-1?
∴a2k+1=2?qk即n=2k-1成立.
可推知n=2k+1也成立.
設(shè)n=2k時,a2k=- qk,則n=2k+2時,由于a2k+2=q?a2k?,
qk,則n=2k+2時,由于a2k+2=q?a2k?,
所以a2k+2=- qk+1,這說明n=2k成立,可推知n=2k+2也成立.
qk+1,這說明n=2k成立,可推知n=2k+2也成立.
綜上所述,對一切自然數(shù)n,猜想都成立.
S2n=(a1+a3…+a2n-1)+(a2+a4+…+a2n)
=2(1+q+q2+…+qn-1?)- (q+q2+…+qn)
(q+q2+…+qn)
依題意知 <3,并注意1-q>0,|q|<1解得-1<q<0或0<q<
<3,并注意1-q>0,|q|<1解得-1<q<0或0<q<
難點31 數(shù)學(xué)歸納法解題
數(shù)學(xué)歸納法是高考考查的重點內(nèi)容之一.類比與猜想是應(yīng)用數(shù)學(xué)歸納法所體現(xiàn)的比較突出的思想,抽象與概括,從特殊到一般是應(yīng)用的一種主要思想方法.
●難點磁場
(★★★★)是否存在a、b、c使得等式1?22+2?32+…+n(n+1)2= (an2+bn+c).
(an2+bn+c).
●案例探究
[例1]試證明:不論正數(shù)a、b、c是等差數(shù)列還是等比數(shù)列,當(dāng)n>1,n∈N*且a、b、c互不相等時,均有:an+cn>2bn.
命題意圖:本題主要考查數(shù)學(xué)歸納法證明不等式,屬★★★★級題目.
知識依托:等差數(shù)列、等比數(shù)列的性質(zhì)及數(shù)學(xué)歸納法證明不等式的一般步驟.
錯解分析:應(yīng)分別證明不等式對等比數(shù)列或等差數(shù)列均成立,不應(yīng)只證明一種情況.
技巧與方法:本題中使用到結(jié)論:(ak-ck)(a-c)>0恒成立(a、b、c為正數(shù)),從而ak+1+ck+1>ak?c+ck?a.
證明:(1)設(shè)a、b、c為等比數(shù)列,a= ,c=bq(q>0且q≠1)
,c=bq(q>0且q≠1)
(2)設(shè)a、b、c為等差數(shù)列,則2b=a+c猜想 >(
>( )n(n≥2且n∈N*)
)n(n≥2且n∈N*)
下面用數(shù)學(xué)歸納法證明:
①當(dāng)n=2時,由2(a2+c2)>(a+c)2,∴
則當(dāng)n=k+1時, (ak+1+ck+1+ak+1+ck+1)
(ak+1+ck+1+ak+1+ck+1)
> (ak+1+ck+1+ak?c+ck?a)=
(ak+1+ck+1+ak?c+ck?a)= (ak+ck)(a+c)
(ak+ck)(a+c)
[例2]在數(shù)列{an}中,a1=1,當(dāng)n≥2時,an,Sn,Sn- 成等比數(shù)列.
成等比數(shù)列.
(1)求a2,a3,a4,并推出an的表達(dá)式;
(2)用數(shù)學(xué)歸納法證明所得的結(jié)論;
(3)求數(shù)列{an}所有項的和.
命題意圖:本題考查了數(shù)列、數(shù)學(xué)歸納法、數(shù)列極限等基礎(chǔ)知識.
知識依托:等比數(shù)列的性質(zhì)及數(shù)學(xué)歸納法的一般步驟.采用的方法是歸納、猜想、證明.
錯解分析:(2)中,Sk=- 應(yīng)舍去,這一點往往容易被忽視.
應(yīng)舍去,這一點往往容易被忽視.
技巧與方法:求通項可證明{ }是以{
}是以{ }為首項,
}為首項, 為公差的等差數(shù)列,進(jìn)而求得通項公式.
為公差的等差數(shù)列,進(jìn)而求得通項公式.
解:∵an,Sn,Sn- 成等比數(shù)列,∴Sn2=an?(Sn-
成等比數(shù)列,∴Sn2=an?(Sn- )(n≥2)
(*)
)(n≥2)
(*)
(1)由a1=1,S2=a1+a2=1+a2,代入(*)式得:a2=-
(2)①當(dāng)n=1,2,3,4時,由(*)知猜想成立.
∴(2k-3)(2k-1)Sk2+2Sk-1=0
由Sk+12=ak+1?(Sk+1- ),得(Sk+ak+1)2=ak+1(ak+1+Sk-
),得(Sk+ak+1)2=ak+1(ak+1+Sk- )
)
(3)由(2)得數(shù)列前n項和Sn= ,∴S=
,∴S= Sn=0.
Sn=0.
●錦囊妙記
(1)數(shù)學(xué)歸納法的基本形式
設(shè)P(n)是關(guān)于自然數(shù)n的命題,若
1°P(n0)成立(奠基)
2°假設(shè)P(k)成立(k≥n0),可以推出P(k+1)成立(歸納),則P(n)對一切大于等于n0的自然數(shù)n都成立.
(2)數(shù)學(xué)歸納法的應(yīng)用
具體常用數(shù)學(xué)歸納法證明:恒等式,不等式,數(shù)的整除性,幾何中計算問題,數(shù)列的通項與和等.
●殲滅難點訓(xùn)練
一、選擇題
1.(★★★★★)已知f(n)=(2n+7)?3n+9,存在自然數(shù)m,使得對任意n∈N,都能使m整除f(n),則最大的m的值為( )
A.30 B.26 C.36 D.6
2.(★★★★)用數(shù)學(xué)歸納法證明3k≥n3(n≥3,n∈N)第一步應(yīng)驗證( )
A.n=1 B.n=2 C.n=3 D.n=4
二、填空題
3.(★★★★★)觀察下列式子: …則可歸納出_________.
…則可歸納出_________.
4.(★★★★)已知a1= ,an+1=
,an+1= ,則a2,a3,a4,a5的值分別為_________,由此猜想an=_________.
,則a2,a3,a4,a5的值分別為_________,由此猜想an=_________.
三、解答題
5.(★★★★)用數(shù)學(xué)歸納法證明4 +3n+2能被13整除,其中n∈N*.
+3n+2能被13整除,其中n∈N*.
7.(★★★★★)已知數(shù)列{bn}是等差數(shù)列,b1=1,b1+b2+…+b10=145.
(1)求數(shù)列{bn}的通項公式bn;
(2)設(shè)數(shù)列{an}的通項an=loga(1+ )(其中a>0且a≠1)記Sn是數(shù)列{an}的前n項和,試比較Sn與
)(其中a>0且a≠1)記Sn是數(shù)列{an}的前n項和,試比較Sn與 logabn+1的大小,并證明你的結(jié)論.
logabn+1的大小,并證明你的結(jié)論.
8.(★★★★★)設(shè)實數(shù)q滿足|q|<1,數(shù)列{an}滿足:a1=2,a2≠0,an?an+1=-qn,求an表達(dá)式,又如果 S2n<3,求q的取值范圍.
S2n<3,求q的取值范圍.
參考答案
難點磁場
解:假設(shè)存在a、b、c使題設(shè)的等式成立,這時令n=1,2,3,有
于是,對n=1,2,3下面等式成立
記Sn=1?22+2?32+…+n(n+1)2
設(shè)n=k時上式成立,即Sk= (3k2+11k+10)
(3k2+11k+10)
那么Sk+1=Sk+(k+1)(k+2)2= (k+2)(3k+5)+(k+1)(k+2)2
(k+2)(3k+5)+(k+1)(k+2)2
也就是說,等式對n=k+1也成立.
綜上所述,當(dāng)a=3,b=11,c=10時,題設(shè)對一切自然數(shù)n均成立.
殲滅難點訓(xùn)練
一、1.解析:∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36
∴f(1),f(2),f(3)能被36整除,猜想f(n)能被36整除.
證明:n=1,2時,由上得證,設(shè)n=k(k≥2)時,
f(k)=(2k+7)?3k+9能被36整除,則n=k+1時,
f(k+1)-f(k)=(2k+9)?3k+1?-(2k+7)?3k
=(6k+27)?3k-(2k+7)?3k
=(4k+20)?3k=36(k+5)?3k-2?(k≥2)
∵f(1)不能被大于36的數(shù)整除,∴所求最大的m值等于36.
答案:C
2.解析:由題意知n≥3,∴應(yīng)驗證n=3.
答案:C
三、5.證明:(1)當(dāng)n=1時,42×1+1+31+2=91能被13整除
(2)假設(shè)當(dāng)n=k時,42k+1+3k+2能被13整除,則當(dāng)n=k+1時,
42(k+1)+1+3k+3=42k+1?42+3k+2?3-42k+1?3+42k+1?3
=42k+1?13+3?(42k+1+3k+2?)
∵42k+1?13能被13整除,42k+1+3k+2能被13整除
∴當(dāng)n=k+1時也成立.
由①②知,當(dāng)n∈N*時,42n+1+3n+2能被13整除.
7.(1)解:設(shè)數(shù)列{bn}的公差為d,由題意得 ,∴bn=3n-2
,∴bn=3n-2
(2)證明:由bn=3n-2知
Sn=loga(1+1)+loga(1+ )+…+loga(1+
)+…+loga(1+ )
)
而 logabn+1=loga
logabn+1=loga ,于是,比較Sn與
,于是,比較Sn與 logabn+1?的大小
logabn+1?的大小 比較(1+1)(1+
比較(1+1)(1+ )…(1+
)…(1+ )與
)與 的大小.
的大小.
①當(dāng)n=1時,已驗證(*)式成立.
②假設(shè)n=k(k≥1)時(*)式成立,即(1+1)(1+ )…(1+
)…(1+ )>
)>
由①②知,(*)式對任意正整數(shù)n都成立.
于是,當(dāng)a>1時,Sn> logabn+1?,當(dāng) 0<a<1時,Sn<
logabn+1?,當(dāng) 0<a<1時,Sn< logabn+1?
logabn+1?
8.解:∵a1?a2=-q,a1=2,a2≠0,
∵an?an+1=-qn,an+1?an+2=-qn+1?
于是,a1=2,a3=2?q,a5=2?qn…猜想:a2n+1=- qn(n=1,2,3,…)
qn(n=1,2,3,…)
下證:(1)當(dāng)n=1,2時猜想成立
(2)設(shè)n=2k-1時,a2k-1=2?qk-1則n=2k+1時,由于a2k+1=q?a2k-1?
∴a2k+1=2?qk即n=2k-1成立.
可推知n=2k+1也成立.
設(shè)n=2k時,a2k=- qk,則n=2k+2時,由于a2k+2=q?a2k?,
qk,則n=2k+2時,由于a2k+2=q?a2k?,
所以a2k+2=- qk+1,這說明n=2k成立,可推知n=2k+2也成立.
qk+1,這說明n=2k成立,可推知n=2k+2也成立.
綜上所述,對一切自然數(shù)n,猜想都成立.
S2n=(a1+a3…+a2n-1)+(a2+a4+…+a2n)
=2(1+q+q2+…+qn-1?)- (q+q2+…+qn)
(q+q2+…+qn)
依題意知 <3,并注意1-q>0,|q|<1解得-1<q<0或0<q<
<3,并注意1-q>0,|q|<1解得-1<q<0或0<q<
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com