
題目列表(包括答案和解析)
解關于 的不等式:
的不等式:

【解析】解:當 時,原不等式可變為
時,原不等式可變為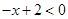 ,即
,即 (2分)
(2分)
當 時,原不等式可變為
時,原不等式可變為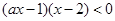
 (5分) 若
(5分) 若 時,
時, 的解為
的解為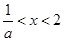 (7分)
(7分)
若 時,
時, 的解為
的解為 (9分) 若
(9分) 若 時,
時, 無解(10分) 若
無解(10分) 若 時,
時, 的解為
的解為 (12分綜上所述
(12分綜上所述
當 時,原不等式的解為
時,原不等式的解為
當 時,原不等式的解為
時,原不等式的解為
當 時,原不等式的解為
時,原不等式的解為
當 時,原不等式的解為
時,原不等式的解為
當 時,原不等式的解為:
時,原不等式的解為: 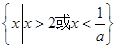
已知 ,設
,設
 和
和 是方程
是方程 的兩個根,不等式
的兩個根,不等式 對任意實數
對任意實數 恒成立;
恒成立; 函數
函數 有兩個不同的零點.求使“P且Q”為真命題的實數
有兩個不同的零點.求使“P且Q”為真命題的實數 的取值范圍.
的取值范圍.
【解析】本試題主要考查了命題和函數零點的運用。由題設x1+x2=a,x1x2=-2,
∴|x1-x2|= =
= .
.
當a∈[1,2]時, 的最小值為3. 當a∈[1,2]時,
的最小值為3. 當a∈[1,2]時, 的最小值為3.
的最小值為3.
要使|m-5|≤|x1-x2|對任意實數a∈[1,2]恒成立,只須|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判別式
=0的判別式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
可得到要使“P∧Q”為真命題,只需P真Q真即可。
解:由題設x1+x2=a,x1x2=-2,
∴|x1-x2|= =
= .
.
當a∈[1,2]時, 的最小值為3.
的最小值為3.
要使|m-5|≤|x1-x2|對任意實數a∈[1,2]恒成立,只須|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判別式
=0的判別式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
綜上,要使“P∧Q”為真命題,只需P真Q真,即
解得實數m的取值范圍是(4,8]
| 3 |
| π |
| 6 |
| π |
| 6 |
( 本題滿分12分) 已知函數

(1)求 的最小正周期、單調增區間、對稱軸和對稱中心;
的最小正周期、單調增區間、對稱軸和對稱中心;
(2)該函數圖象可由 的圖象經過怎樣的平移和伸縮變換得到?
的圖象經過怎樣的平移和伸縮變換得到?
(1)證明F(x)可化為Φ(x0)計算.
(2)利用正態曲線的性質說明:當x取何值時,正態總體N(μ,σ2)相應的函數f(x)=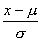 (x∈R)有最大值,其最大值是多少?
(x∈R)有最大值,其最大值是多少?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com