精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

如圖,三棱錐中,側(cè)面底面, ,且,.(Ⅰ)求證:平面;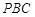

(Ⅱ)若為側(cè)棱PB的中點(diǎn),求直線AE與底面所成角的正弦值.

【解析】第一問(wèn)中，利用由知, ,

又AP=PC=2,所以AC=2,

又AB=4, BC=2,,所以,所以,即,

又平面平面ABC,平面平面ABC=AC, 平面ABC,

平面ACP,所以第二問(wèn)中結(jié)合取AC中點(diǎn)O,連接PO、OB,并取OB中點(diǎn)H,連接AH、EH,因?yàn)镻A=PC,所以PO⊥AC,同(Ⅰ)易證平面ABC,又EH//PO,所以EH平面ABC ,

則為直線AE與底面ABC 所成角,

解

 (Ⅰ) 證明:由用由知, ,

又AP=PC=2,所以AC=2,

又AB=4, BC=2,,所以,所以,即,

又平面平面ABC,平面平面ABC=AC, 平面ABC,

平面ACP,所以

………………………………………………6分

(Ⅱ)如圖, 取AC中點(diǎn)O,連接PO、OB,并取OB中點(diǎn)H,連接AH、EH,

因?yàn)镻A=PC,所以PO⊥AC,同(Ⅰ)易證平面ABC,

又EH//PO,所以EH平面ABC ,

則為直線AE與底面ABC 所成角,

且………………………………………10分

又PO=1/2AC=,也所以有EH=1/2PO=,

由(Ⅰ)已證平面PBC,所以,即,

故,

于是

所以直線AE與底面ABC 所成角的正弦值為

 

已知橢圓x²+by²=3a與直線x+y-1=0相交于A、B兩點(diǎn)
（1）當(dāng)時(shí)，求實(shí)數(shù)b的取值范圍；
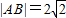（2）當(dāng)時(shí)，AB的中點(diǎn)M與橢圓中心連線的斜率為時(shí)，求橢圓的方程．

已知橢圓

x2

a2

+y²=1（a≥2），直線l與橢圓交于A、B兩點(diǎn)，M是線段AB的中點(diǎn)，連接OM并延長(zhǎng)交橢圓于點(diǎn)C．
（Ⅰ）設(shè)直線AB與直線OM的斜率分別為k₁、k₂，且k₁•k₂=-

1

2

，求橢圓的離心率．
（Ⅱ）若直線AB經(jīng)過(guò)橢圓的右焦點(diǎn)F，且四邊形OACB是平行四邊形，求直線AB斜率的取值范圍．

在任意八邊形ABCDEFGT中，取各邊中點(diǎn)，如圖，H、I、J、K、L、M、N、O分別是GT、TA、AB、BC、CD、DE、EF、FG的中點(diǎn)，連接IK、JL、MO、NH，P、Q、R、S分別是NH、MO、JL、IK的中點(diǎn)．求證：以P、Q、R、S為頂點(diǎn)的四邊形SRQP是平行四邊形．

（本題滿分13分）學(xué)科網(wǎng) 已知橢圓，直線與橢圓交于、兩點(diǎn)，是線段的中點(diǎn)，連接并延長(zhǎng)交橢圓于點(diǎn)．設(shè)直線與直線的斜率分別為、，且，求橢圓的離心率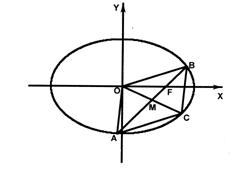． 若直線經(jīng)過(guò)橢圓的右焦點(diǎn)，且四邊形是平行四邊形，求直線斜率的取值范圍．學(xué)科網(wǎng)

學(xué)科網(wǎng)