
題目列表(包括答案和解析)
在△ABC中,已知AB=,BC=2。
(Ⅰ)若cosB=-,求sinC的值;
(Ⅱ)求角C的取值范圍.
在△ABC中,已知AB=,BC=2。
(Ⅰ)若cosB=-,求sinC的值;
(Ⅱ)求角C的取值范圍.
已知函數 , 其中
, 其中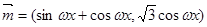
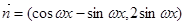 ,其中
,其中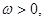 若
若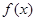 相鄰兩對稱軸間的距離不小于
相鄰兩對稱軸間的距離不小于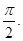
(1)求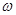 的取值范圍;
的取值范圍;
(2)在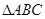 中,
中,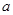 、
、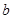 、
、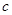 分別是角A、B、C的對邊,
分別是角A、B、C的對邊,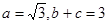 ,當
,當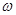 最大時,
最大時,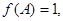 求
求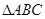 的面積。
的面積。
已知函數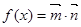 , 其中
, 其中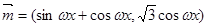 ,
,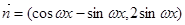 ,其中
,其中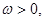 若
若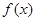 相鄰兩對稱軸間的距離不小于
相鄰兩對稱軸間的距離不小于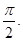
(1)求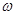 的取值范圍;
的取值范圍;
(2)在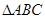 中,
中,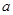 、
、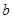 、
、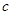 分別是角A、B、C的對邊,
分別是角A、B、C的對邊,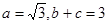 ,當
,當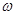 最大時,
最大時,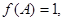 求
求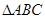 的面積。
的面積。
已知 其中
其中 ,
,
 ,若
,若 圖象中相鄰的兩條對稱軸間的距離不小于
圖象中相鄰的兩條對稱軸間的距離不小于 。
。
(1)求 的取值范圍
的取值范圍
(2)在 中,a,b,c分別為角A,B,C的對邊,
中,a,b,c分別為角A,B,C的對邊, 。當
。當 取最大值時,f(A)=1,求b,c的值。
取最大值時,f(A)=1,求b,c的值。
 1.1 2.
1.1 2. 3.
3. 4.-8 5.
4.-8 5. 6.20
7.
6.20
7.
 8.1 9.0 10.
8.1 9.0 10. 11.
11. 12.
12. 13.
13. 14.(1005,1004)
14.(1005,1004)
 15.⑴ ∵
15.⑴ ∵ 
 ,……………………………… 2分
,……………………………… 2分
 又∵
又∵  ,∴
,∴  而
而 為斜三角形,
為斜三角形,
 ∵
∵ ,∴
,∴ . ……………………………………………………………… 4分
. ……………………………………………………………… 4分
∵ ,∴
,∴ . …………………………………………………… 6分
. …………………………………………………… 6分
⑵∵ ,∴
,∴ …12分
…12分
即 ,∵
,∵ ,∴
,∴ .…………………………………14分
.…………………………………14分
16.⑴∵ 平面
平面 ,
, 平面
平面 ,所以
,所以 ,…2分
,…2分
∵ 是菱形,∴
是菱形,∴ ,又
,又 ,
,
∴ 平面
平面 ,……………………………………………………4分
,……………………………………………………4分
又∵ 平面
平面 ,∴平面
,∴平面 平面
平面 . ……………………………………6分
. ……………………………………6分

 ⑵取
⑵取 中點
中點 ,連接
,連接 ,則
,則 ,
,
∵ 是菱形,∴
是菱形,∴ ,
,
∵ 為
為 的中點,∴
的中點,∴ ,………………10分
,………………10分
∴ .
.
∴四邊形 是平行四邊形,∴
是平行四邊形,∴ ,………………12分
,………………12分
又∵ 平面
平面 ,
, 平面
平面 .
.
∴ 平面
平面 . ………………………………………………………………14分
. ………………………………………………………………14分
17.(1)∵直線 過點
過點 ,且與圓
,且與圓 :
: 相切,
相切,
設直線 的方程為
的方程為 ,即
,即 , …………………………2分
, …………………………2分
則圓心 到直線
到直線 的距離為
的距離為 ,解得
,解得 ,
,
∴直線 的方程為
的方程為 ,即
,即 . …… …………………4分
. …… …………………4分
(2)對于圓方程 ,令
,令 ,得
,得 ,即
,即 .又直線
.又直線 過點
過點 且與
且與 軸垂直,∴直線
軸垂直,∴直線 方程為
方程為 ,設
,設 ,則直線
,則直線 方程為
方程為
解方程組 ,得
,得 同理可得,
同理可得, ……………… 10分
……………… 10分
∴以 為直徑的圓
為直徑的圓 的方程為
的方程為 ,
,
又 ,∴整理得
,∴整理得 ,……………………… 12分
,……………………… 12分
若圓 經過定點,只需令
經過定點,只需令 ,從而有
,從而有 ,解得
,解得 ,
,
∴圓 總經過定點坐標為
總經過定點坐標為 . …………………………………………… 14分
. …………………………………………… 14分
18.⑴因為當 時,
時, ,所以
,所以 , ……4分
, ……4分
∴ ………………………………………………………6分
………………………………………………………6分
⑵設每小時通過的車輛為 ,則
,則 .即
.即
 ……12分
……12分
∵ ,…………………………………………………14分
,…………………………………………………14分
 ∴
∴ ,當且僅當
,當且僅當 ,即
,即 時,
時, 取最大值
取最大值 .
.
答:當 時,大橋每小時通過的車輛最多.………16分
時,大橋每小時通過的車輛最多.………16分
19.(1)由 ,得
,得
∴b、c所滿足的關系式為 .……………………2分
.……………………2分
(2)由 ,
, ,可得
,可得 .
.
方程 ,即
,即 ,可化為
,可化為 ,
,
令 ,則由題意可得,
,則由題意可得, 在
在 上有唯一解,…4分
上有唯一解,…4分
令
 ,由
,由 ,可得
,可得 ,
,
當 時,由
時,由 ,可知
,可知 是增函數;
是增函數;
當 時,由
時,由 ,可知
,可知 是減函數.故當
是減函數.故當 時,
時, 取極大值
取極大值 .………6分
.………6分
由函數 的圖象可知,當
的圖象可知,當 或
或 時,方程
時,方程 有且僅有一個正實數解.
有且僅有一個正實數解.
故所求 的取值范圍是
的取值范圍是 或
或 . ……………………………………………8分
. ……………………………………………8分
(3)由 ,
, ,可得
,可得 .由
.由 且
且
 且
且
 且
且 .…10分
.…10分
當 時,
時,  ;當
;當 時,
時, ;
;
當 時(
時( ),
), ;當
;當 時,
時,
 且
且 ;
;
當 時,
時, ∪
∪ . ………………………16分
. ………………………16分
注:可直接通過研究函數 與
與 的圖象來解決問題.
的圖象來解決問題.
20.(1)由 ,且等差數列
,且等差數列 的公差為
的公差為 ,可知
,可知 ,
,
若插入的一個數在 之間,則
之間,則 ,
, ,
,
消去 可得
可得 ,其正根為
,其正根為 . ………………………………2分
. ………………………………2分
若插入的一個數在 之間,則
之間,則 ,
, ,
,
消去 可得
可得 ,此方程無正根.故所求公差
,此方程無正根.故所求公差 .………4分
.………4分
(2)設在 之間插入
之間插入 個數,在
個數,在 之間插入
之間插入 個數,則
個數,則 ,在等比數列
,在等比數列 中,
中,
∵ ,
, …,
…, ,
,
∴ …
… …
… ………………8分
………………8分
又∵ ,
, ,
, 都為奇數,∴
都為奇數,∴ 可以為正數,也可以為負數.
可以為正數,也可以為負數.
①若 為正數,則
為正數,則 …
… ,所插入
,所插入 個數的積為
個數的積為 ;
;
②若 為負數,
為負數, …
… 中共有
中共有 個負數,
個負數,
當 是奇數,即
是奇數,即 N*)時,所插入
N*)時,所插入 個數的積為
個數的積為 ;
;
當 是偶數,即
是偶數,即 N*)時,所插入
N*)時,所插入 個數的積為
個數的積為 .
.
綜上所述,當 N*)時,所插入
N*)時,所插入 個數的積為
個數的積為 ;
;
當 N*)時,所插入
N*)時,所插入 個數的積為
個數的積為 .…………10分
.…………10分
注:可先將 …
… 用
用 和
和 表示,然后再利用條件消去
表示,然后再利用條件消去 進行求解.
進行求解.
(3)∵在等比數列 ,由
,由 ,可得
,可得 ,同理可得
,同理可得 ,
,
∴ ,即
,即
 , …………………………12分
, …………………………12分
假設 是有理數,若
是有理數,若 為整數,∵
為整數,∵ 是正數,且
是正數,且 ,∴
,∴ ,
,
在 中,∵
中,∵ 是
是 的倍數,故1也是
的倍數,故1也是 的倍數,矛盾.
的倍數,矛盾.
若 不是整數,可設
不是整數,可設 (其中
(其中 為互素的整數,
為互素的整數, ),
),
則有 ,即
,即 ,
,
∵ ,可得
,可得 ,∴
,∴ 是x的倍數,即
是x的倍數,即 是x的倍數,矛盾.
是x的倍數,矛盾.
∴  是無理數.……………………………………16分
是無理數.……………………………………16分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com