
題目列表(包括答案和解析)
(本小題共13分)
已知集合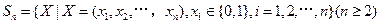 對于
對于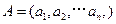 ,
,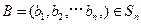 ,定義A與B的差為
,定義A與B的差為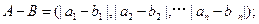
A與B之間的距離為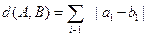
(Ⅰ)證明: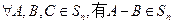 ,且
,且 ;
;
(Ⅱ)證明: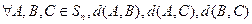 三個數中至少有一個是偶數
三個數中至少有一個是偶數
(Ⅲ) 設P ,P中有m(m≥2)個元素,記P中所有兩元素間距離的平均值為
,P中有m(m≥2)個元素,記P中所有兩元素間距離的平均值為 (P).
(P). 證明:
證明: (P)≤
(P)≤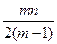 .
.
(考生務必將答案答在答題卡上,在試卷上作答無效)
已知a、b、c是互不相等的非零實數.若用反證法證明三個方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一個方程有兩個相異實根.
【解析】本試題主要考查了二次方程根的問題的綜合運用。運用反證法思想進行證明。
先反設,然后推理論證,最后退出矛盾。證明:假設三個方程中都沒有兩個相異實根,
則Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0.顯然不成立。
證明:假設三個方程中都沒有兩個相異實根,
則Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0.
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0. ①
由題意a、b、c互不相等,∴①式不能成立.
∴假設不成立,即三個方程中至少有一個方程有兩個相異實根.
已知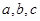 均為實數,且
均為實數,且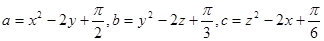 ,
,
求證: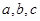 中至少有一個大于
中至少有一個大于 。
。
【解析】利用反證法的思想進行證明即可。首先否定結論假設a,b,c都不大于0然后在假設的前提下,即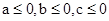 ,得
,得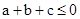 ,而
,而 ,即
,即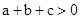 ,與
,與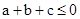 矛盾從而得到矛盾,假設不成立。
矛盾從而得到矛盾,假設不成立。
| 方式 | 實施地點 | 大雨 | 中雨 | 小雨 | 摸擬試驗總次數 |
| A | 甲 | 4次 | 6次 | 2次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
某研究小組在電腦上進行人工降雨摸擬試驗,準備用 三種人工降雨方式分別對甲、乙、丙三地實施人工降雨,其試驗數據統計如下:
三種人工降雨方式分別對甲、乙、丙三地實施人工降雨,其試驗數據統計如下:
|
方式 |
實施地點 |
大雨 |
中雨 |
小雨 |
摸擬試驗總次數 |
|
|
甲 |
4次 |
6次 |
2次 |
12次 |
|
|
乙 |
3次 |
6次 |
3次 |
12次 |
|
|
丙 |
2次 |
2次 |
8次 |
12次 |
假設甲、乙、丙三地實施的人工降雨彼此互不影響.
(Ⅰ)求甲、乙兩地恰為中雨且丙地為小雨的概率;
(Ⅱ)考慮到旱情和水土流失,如果甲地恰需中雨即能達到理想狀態,乙地必須是大雨才能達到理想狀態,丙地只要是小雨或中雨就能達到理想狀態,求甲、乙、丙三地中至少有兩地降雨量達到理想狀態的概率.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com