
題目列表(包括答案和解析)
設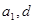 為實數,首項為
為實數,首項為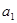 ,公差為
,公差為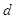 的等差數列
的等差數列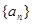 的前n項和為
的前n項和為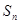 ,滿足
,滿足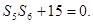
(1)若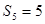 ,求
,求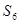 及
及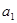 ;
;
(2)求d的取值范圍.
【解析】本試題主要考查了數列的求和的運用以及通項公式的運用。第一問中,利用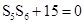 和已知的
和已知的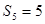 ,得到結論
,得到結論
第二問中,利用首項和公差表示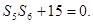 ,則方程是一個有解的方程,因此判別式大于等于零,因此得到d的范圍。
,則方程是一個有解的方程,因此判別式大于等于零,因此得到d的范圍。
解:(1)因為設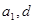 為實數,首項為
為實數,首項為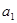 ,公差為
,公差為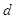 的等差數列
的等差數列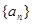 的前n項和為
的前n項和為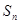 ,滿足
,滿足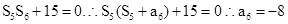
所以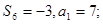
(2)因為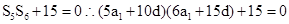
得到關于首項的一個二次方程,則方程必定有解,結合判別式求解得到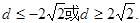
一支車隊有15輛車,某天依次出發執行運輸任務,第一輛車于下午2時出發,第二輛車于下午2時10分出發,第三輛車于下午2時20分出發,依此類推。假設所有的司機都連續開車,并都在下午6時停下來休息。
(1)到下午6時最后一輛車行駛了多長時間?
(2)如果每輛車的行駛速度都是60 ,這個車隊當天一共行駛了多少千米?
,這個車隊當天一共行駛了多少千米?
【解析】第一問中,利用第一輛車出發時間為下午2時,每隔10分鐘即 小時出發一輛
小時出發一輛
則第15輛車在 小時,最后一輛車出發時間為:
小時,最后一輛車出發時間為: 小時
小時
第15輛車行駛時間為: 小時(1時40分)
小時(1時40分)
第二問中,設每輛車行駛的時間為: ,由題意得到
,由題意得到
 是以
是以 為首項,
為首項, 為公差的等差數列
為公差的等差數列
則行駛的總時間為:
則行駛的總里程為: 運用等差數列求和得到。
運用等差數列求和得到。
解:(1)第一輛車出發時間為下午2時,每隔10分鐘即 小時出發一輛
小時出發一輛
則第15輛車在 小時,最后一輛車出發時間為:
小時,最后一輛車出發時間為: 小時
小時
第15輛車行駛時間為: 小時(1時40分)
……5分
小時(1時40分)
……5分
(2)設每輛車行駛的時間為: ,由題意得到
,由題意得到
 是以
是以 為首項,
為首項, 為公差的等差數列
為公差的等差數列
則行駛的總時間為: ……10分
……10分
則行駛的總里程為:
一、選擇題
1. D
解析:∵a3+a7+a11=3a7為常數,
∴S13= =13a7,也是常數.
=13a7,也是常數.
2. C
解析:∵易知q≠1,S6∶S3=1∶2
 =
= ,q3=-
,q3=- ,
,
∴S9∶S3= =1+q3+q6=1-
=1+q3+q6=1- +(-
+(- )2=
)2= .
.
3.A  ,
,
又


4.D 數列 是以2為首項,以
是以2為首項,以 為公比的等比數列,項數為
為公比的等比數列,項數為 故選D。
故選D。
5.B
6. D
解析:當q=1時,Sn,Sn+1,Sn+2構成等差數列;
當q=-2時,Sn+1,Sn,Sn+2構成等差數列;
當q=- 時,Sn,Sn+2,Sn+1構成等差數列.
時,Sn,Sn+2,Sn+1構成等差數列.
7.A 僅②不需要分情況討論,即不需要用條件語句
8. D
9. D
解析:易知an=
∴a13+a23+…+an3=23+81+82+…+8n-1=8+ =
= (8n-1+6).
(8n-1+6).
10.A提示:依題意 可得.
可得.
11.B, 指輸入的數據.
指輸入的數據.
12.D
(法一)輾轉相除法:


∴ 是
是 和
和 的最大公約數.
的最大公約數.
(法二)更相減損術:





 ∴
∴ 是
是 和
和 的最大公約數.
的最大公約數.
二、填空題
13.

14. 

當 時,
時, 是正整數。
是正整數。
15.
解析:bn= =
= =a1
=a1 ,bn+1=a1
,bn+1=a1 ,
, =
= (常數).
(常數).
16.-6
三、解答題
17.解(1)

 以3為公比的等比數列.
以3為公比的等比數列.
(2)由(1)知, .
. .
.
 不適合上式,
不適合上式,
 .
.
18.解:(1)an=
 (2)
(2) .
.
19.解:(1) ,
, ;
;
(2)由(1)得 ,假設數列{bn}中存在三項bp,bq,br(p,q,r互不相等)成等比數列,則
,假設數列{bn}中存在三項bp,bq,br(p,q,r互不相等)成等比數列,則 即
即
∴ ,
, ,
, ,得
,得
∴p=r,矛盾. ∴數列{bn}中任意三項都不可能成等比數列.
20.解:設未贈禮品時的銷售量為a0個,而贈送禮品價值n元時銷售量為an個,
 ,
,
又設銷售利潤為數列 ,
,
當 ,
,
考察 的單調性,
的單調性,

 當n=9或10時,
當n=9或10時, 最大
最大
答:禮品價值為9元或10元時商品獲得最大利潤.
21.解析:(1) 時,
時,
 即
即
兩式相減:
即 故有
故有
 。
。
 數列
數列 為首項
為首項 公比
公比 的等比數列。
的等比數列。

(2)
 則
則

又
(3)
 ①
①
而 ②
②
①-②得:

22.解:(1)b4=b1+3d 即11=2+3d, ∴b1=2,
b2=5, b3=8, b4=11,
b5=8, b6=5, b7=2;
∴b1=2,
b2=5, b3=8, b4=11,
b5=8, b6=5, b7=2;
(2)S=C1+C2+…+C49=2(C25+C26+…+C49)-C25= ;
;
(3) ,d100=2+3×49=149,∴d1, d2,…d50是首項為149,公差為-3的等差數列.
,d100=2+3×49=149,∴d1, d2,…d50是首項為149,公差為-3的等差數列.
當n≤50時,
當51≤n≤100時,Sn=d1+d2+…d50=S50+(d51+d52+…dn)
=3775+(n-50)×2+ =
=
∴綜上所述, .
.
w.w.w.k.s.5.u.c.o.m

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com