
題目列表(包括答案和解析)
已知直線 和平面
和平面 , 則下列命題正確的是
, 則下列命題正確的是
A.若 ∥
∥ ,
, ,則
,則 ∥
∥ B.若
B.若 ∥
∥ ,
, ,則
,則 ∥
∥
C.若 ⊥
⊥ ,
, ,則
,則 ⊥
⊥ D.若
D.若 ⊥
⊥ ,
, ⊥
⊥ ,則
,則 ∥
∥
已知直線 和平面
和平面 ,在下列命題中真命題是
,在下列命題中真命題是
A.
若 內有無數多條直線垂直于
內有無數多條直線垂直于 內的一條直線,則
內的一條直線,則
B. 若 內有不共線的三點到
內有不共線的三點到 的距離相等,則
的距離相等,則
C. 若 是兩條相交直線,
是兩條相交直線, ,
, ,則
,則
D. 若
已知直線 和平面
和平面 .給定下列四個命題:
.給定下列四個命題:
①若 ∥
∥ ,
, ,那么
,那么 ∥
∥ ;
;
②若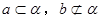 ,且
,且 ,則
,則 ;
;
③若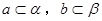 ,且
,且 ,則
,則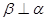 ;
;
④若 ,且
,且 ∥
∥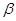 ,
, ∥
∥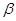 ,則
,則 ∥
∥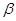 .
.
其中真命題的序號是
A.①② B.①
C.①④ D.③
已知直線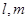 和平面
和平面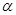 , 則下列命題正確的是
, 則下列命題正確的是
A.若 ∥ ∥ , ,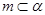 ,則 ,則 ∥ ∥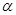 | B.若 ∥ ∥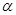 , ,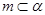 ,則 ,則 ∥ ∥ |
C.若 ⊥ ⊥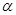 , ,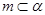 ,則 ,則 ⊥ ⊥ | D.若 ⊥ ⊥ , , ⊥ ⊥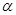 ,則 ,則 ∥ ∥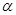 |
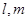 和平面
和平面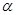 , 則下列命題正確的是
, 則下列命題正確的是A.若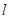 ∥ ∥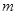 , ,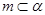 ,則 ,則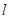 ∥ ∥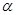 | B.若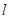 ∥ ∥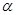 , ,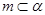 ,則 ,則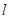 ∥ ∥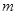 |
C.若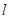 ⊥ ⊥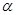 , ,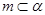 ,則 ,則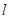 ⊥ ⊥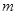 | D.若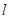 ⊥ ⊥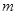 , ,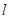 ⊥ ⊥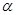 ,則 ,則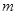 ∥ ∥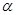 |
第 Ⅰ 卷(共50分)
一、選擇題:
題號
1
2
3
4
5
6
7
8
9
10
答案
B
B
C
C
A
B
D
D
C
A
二、填空題:
11. 20 12. 4 13. 22 14. 24 15. 
三、解答題:
16.解:(1)由 得
得
 ………………………………………2分
………………………………………2分




 …………………………6分
…………………………6分
(2)




 …………………………10分
…………………………10分



 ……………12分
……………12分
 17.解:(1)取SA的中點H,連結EH,BH
17.解:(1)取SA的中點H,連結EH,BH
 E是SD的中點
E是SD的中點




 四邊形EFBH為平行四邊形
四邊形EFBH為平行四邊形
 又
又
 ………………………4分
………………………4分
(2)


以 為原點,
為原點, 為
為 軸,
軸, 為
為 軸,
軸, 為
為 軸,如圖所示建立直角坐標系,
軸,如圖所示建立直角坐標系,
則

設 是平面
是平面 的法向量,則
的法向量,則


 取
取
則 到平面
到平面 的距離為
的距離為 …………………………8分
…………………………8分
(3)設 ,則
,則


設 是平面
是平面 的法向量,則
的法向量,則

 取
取
由 得
得
 , 故存在G點滿足要求,
, 故存在G點滿足要求, .
…………………………12分
.
…………………………12分
18.解:


由已知,得
 …………………………3分
…………………………3分
(1)
由 ,得
,得 或
或
由 ,得
,得
 的遞增區間是
的遞增區間是 ,遞減區間是
,遞減區間是 ……………………6分
……………………6分
(2)不等式即 


由 ,得
,得
又


 在
在 內最大值為6,最小值為-14
內最大值為6,最小值為-14


 的取值范圍為
的取值范圍為 …………………………12分
…………………………12分
19.解:(1) …………………………2分
…………………………2分


 隨
隨 的增大而增大
的增大而增大
 當
當 時,
時, …………………………6分
…………………………6分
(2)連續操作四次“獲勝”的概率記作 ,則
,則



當且僅當  即
即 時取“=”
時取“=”
由 ,得
,得


 當
當 時,“獲勝”的概率最大.
…………………………12分
時,“獲勝”的概率最大.
…………………………12分
20.解:設A、B的坐標分別為
 的方程為:
的方程為:
(1)N點坐標





所求 的方程為:
的方程為: …………………………6分
…………………………6分
(2)由 得
得 

 ,
, ,
, 



設 點坐標為
點坐標為 , 顯然
, 顯然 




 …………………………13分
…………………………13分
21.解:(1)欲使 為等差數列,只需
為等差數列,只需
即 
令 得
得 
 存在實數
存在實數 ,使
,使 是等差數列.
…………………………3分
是等差數列.
…………………………3分
(2)

 是等差數列,
是等差數列,


 …………………………5分
…………………………5分




故 …………………………8分
…………………………8分
(3)當 時,
時,
又 ,
,


 左式
左式 .
…………………………14分
.
…………………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com