
題目列表(包括答案和解析)
把函數 的圖象按向量
的圖象按向量 平移得到函數
平移得到函數 的圖象.
的圖象.
(1)求函數 的解析式; (2)若
的解析式; (2)若 ,證明:
,證明: .
.
【解析】本試題主要考查了函數 平抑變換和運用函數思想證明不等式。第一問中,利用設 上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入
上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入 ,便可以得到結論。第二問中,令
,便可以得到結論。第二問中,令 ,然后求導,利用最小值大于零得到。
,然后求導,利用最小值大于零得到。
(1)解:設 上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入
上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 證明:令 ,……6分
,……6分
則 ……8分
……8分
 ,∴
,∴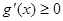 ,∴
,∴ 在
在 上單調遞增.……10分
上單調遞增.……10分
故 ,即
,即
已知點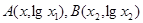 是函數
是函數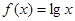 的圖象上任意不同兩點,依據圖象可知,段段AB總是位于A,B兩點之間函數圖象的下方,因此有結論
的圖象上任意不同兩點,依據圖象可知,段段AB總是位于A,B兩點之間函數圖象的下方,因此有結論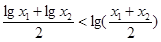 成立。運用類比思想方法可知,若點
成立。運用類比思想方法可知,若點 ,
, 是函數
是函數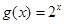 的圖象上的不同兩點,則類似地有成立 。
的圖象上的不同兩點,則類似地有成立 。
將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位,得到函數
個單位,得到函數![]() 即
即![]() 的圖象,再向上平移1個單位,所得圖象的函數解析式為
的圖象,再向上平移1個單位,所得圖象的函數解析式為![]() ,故選B.
,故選B.
答案:B
【命題立意】:本題考查三角函數的圖象的平移和利用誘導公式及二倍角公式進行化簡解析式的基本知識和基本技能,學會公式的變形. w.w.w.k.s.5.u.c.o.m
已知函數 。
。
(1)求函數的最小正周期和最大值;
(2)求函數的增區間;
(3)函數的圖象可以由函數 的圖象經過怎樣的變換得到?
的圖象經過怎樣的變換得到?
【解析】本試題考查了三角函數的圖像與性質的運用。第一問中,利用 可知函數的周期為
可知函數的周期為 ,最大值為
,最大值為 。
。
第二問中,函數 的單調區間與函數
的單調區間與函數 的單調區間相同。故當
的單調區間相同。故當 ,解得x的范圍即為所求的區間。
,解得x的范圍即為所求的區間。
第三問中,利用圖像將 的圖象先向右平移
的圖象先向右平移 個單位長度,再把橫坐標縮短為原來的
個單位長度,再把橫坐標縮短為原來的 (縱坐標不變),然后把縱坐標伸長為原來的
(縱坐標不變),然后把縱坐標伸長為原來的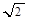 倍(橫坐標不變),再向上平移1個單位即可。
倍(橫坐標不變),再向上平移1個單位即可。
解:(1)函數 的最小正周期為
的最小正周期為 ,最大值為
,最大值為 。
。
(2)函數 的單調區間與函數
的單調區間與函數 的單調區間相同。
的單調區間相同。
 即
即
 所求的增區間為
所求的增區間為 ,
,
 即
即
 所求的減區間為
所求的減區間為 ,
, 。
。
(3)將 的圖象先向右平移
的圖象先向右平移 個單位長度,再把橫坐標縮短為原來的
個單位長度,再把橫坐標縮短為原來的 (縱坐標不變),然后把縱坐標伸長為原來的
(縱坐標不變),然后把縱坐標伸長為原來的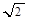 倍(橫坐標不變),再向上平移1個單位即可。
倍(橫坐標不變),再向上平移1個單位即可。
已知函數
(1)若函數 的圖象經過P(3,4)點,求a的值;
的圖象經過P(3,4)點,求a的值;
(2)比較 大小,并寫出比較過程;
大小,并寫出比較過程;
(3)若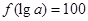 ,求a的值.
,求a的值.
【解析】本試題主要考查了指數函數的性質的運用。第一問中,因為函數 的圖象經過P(3,4)點,所以
的圖象經過P(3,4)點,所以 ,解得
,解得 ,因為
,因為 ,所以
,所以 .
.
(2)問中,對底數a進行分類討論,利用單調性求解得到。
(3)中,由 知,
知, .,指對數互化得到
.,指對數互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函數 的圖象經過
的圖象經過 ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵當 時,
時, ;
;
當 時,
時, . ……………… 6分
. ……………… 6分
因為, ,
,
當 時,
時, 在
在 上為增函數,∵
上為增函數,∵ ,∴
,∴ .
.
即 .當
.當 時,
時, 在
在 上為減函數,
上為減函數,
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com