
題目列表(包括答案和解析)
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| y2 |
| t |
| n |
| OA |
| OB |
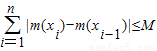 恒成立,則稱函數m(x)為在[p,q]上的有界變差函數,試判斷函數f(x)是否為在[1,3]上的有界變差函數?若是,求M的最小值;若不是,請說明理由.(參考公式:
恒成立,則稱函數m(x)為在[p,q]上的有界變差函數,試判斷函數f(x)是否為在[1,3]上的有界變差函數?若是,求M的最小值;若不是,請說明理由.(參考公式: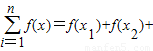 …+f(xn))
…+f(xn))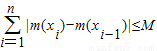 恒成立,則稱函數m(x)為在[p,q]上的有界變差函數,試判斷函數f(x)是否為在[1,3]上的有界變差函數?若是,求M的最小值;若不是,請說明理由.(參考公式:
恒成立,則稱函數m(x)為在[p,q]上的有界變差函數,試判斷函數f(x)是否為在[1,3]上的有界變差函數?若是,求M的最小值;若不是,請說明理由.(參考公式: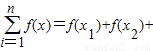 …+f(xn))
…+f(xn))湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com