
題目列表(包括答案和解析)
已知數列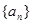 的前n項和
的前n項和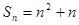 ,數列
,數列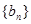 有
有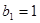 ,
,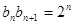
(1)求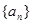 的通項;
的通項;
(2)若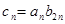 ,求數列
,求數列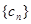 的前n項和
的前n項和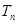 .
.
【解析】第一問中,利用當n=1時,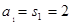
當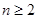 時,
時,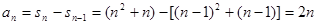
得到通項公式
第二問中,∵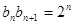 ∴
∴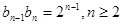 ∴數列
∴數列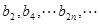 是以2為首項,2為公比的等比數列,利用錯位相減法得到。
是以2為首項,2為公比的等比數列,利用錯位相減法得到。
解:(1)當n=1時,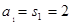 ……………………1分
……………………1分
當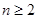 時,
時,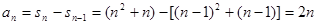 ……4分
……4分
又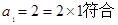
∴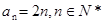 ……………………5分
……………………5分
(2)∵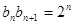 ∴
∴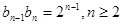
∴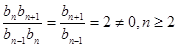 ……………………7分
……………………7分
又∵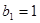 ,
,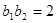 ∴
∴ 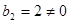
∴數列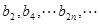 是以2為首項,2為公比的等比數列,
是以2為首項,2為公比的等比數列,
∴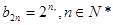 ……………………9分
……………………9分
∴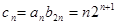
∴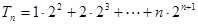 ①
①
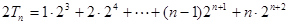 ②
②
①-②得: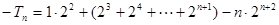
∴
(本小題滿分13分)
隨機變量X的分布列如下表如示,若數列 是以
是以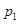 為首項,以
為首項,以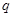 為公比的等比數列,則稱隨機變量X服從等比分布,記為Q(
為公比的等比數列,則稱隨機變量X服從等比分布,記為Q(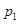 ,
,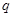 ).現隨機變量X∽Q(
).現隨機變量X∽Q( ,2).
,2).
|
X |
1 |
2 |
… |
n |
|
|
|
|
… |
|
(Ⅰ)求n 的值并求隨機變量X的數學期望EX;
(Ⅱ)一個盒子里裝有標號為1,2,…,n且質地相同的標簽若干張,從中任取1張標簽所得的標號為隨機變量X.現有放回的從中每次抽取一張,共抽取三次,求恰好2次取得標簽的標號不大于3的概率.
(本小題滿分13分)
隨機變量X的分布列如下表如示,若數列 是以
是以 為首項,以
為首項,以 為公比的等比數列,則稱隨機變量X服從等比分布,記為Q(
為公比的等比數列,則稱隨機變量X服從等比分布,記為Q( ,
, ).現隨機變量X∽Q(
).現隨機變量X∽Q( ,2).
,2).
|
X |
1 |
2 |
… |
n |
|
|
|
|
… |
|
(Ⅰ)求n 的值并求隨機變量X的數學期望EX;
(Ⅱ)一個盒子里裝有標號為1,2,…,n且質地相同的標簽若干張,從中任取1張標簽所得的標號為隨機變量X.現有放回的從中每次抽取一張,共抽取三次,求恰好2次取得標簽的標號不大于3的概率.
如圖是一個具有n行n列的數表,第一行是首項為1,公比為q的等比數列,第一列是首項為1,公差為d的等差數列,其它空格按照“任意一格的數是它上面一格的數與它左邊一格的數之和”的規則填寫.設aij表示第i行第j列的數.
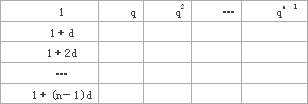
(1)求a22,a32及an2的表達式;
(2)第二行能否構成等比數列?若能,求出q,d滿足的條件;若不能,請說明理由.
(3)請根據這張數表提出一個與問題(2)相類似的問題,并加以研究和解決(根據所提問題的難度及解答情況評分).
某項游戲活動的獎勵分成一、二、三等獎且相應獲獎概率是以![]() 為首項公比為2的等比數列,相應獲得的獎金是以700元為首項,公差為
為首項公比為2的等比數列,相應獲得的獎金是以700元為首項,公差為![]() 元的等差數列,則參與該游戲獲得獎金的期望為________元。
元的等差數列,則參與該游戲獲得獎金的期望為________元。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com