
�}Ŀ�б�(�����𰸺ͽ���)
����С�}�M��12�֣�ijِ�����ס��҃����@���\(y��n)��(d��ng)�T��������10��(ch��ng)��ِ����ِ�÷���rӛ����£���λ���֣���
�ף�37��21��31��20��29��19��32��23��25��33
�ң�10��30��47��27��46��14��26��10��44��46
������(j��)�÷���rӛ䛣����������@���\(y��n)��(d��ng)�T�÷ֵ��o�~�D��������(j��)�o�~�D����(du��)�ס��҃��\(y��n)��(d��ng)�T�÷������^����(xi��)���ɂ�(g��)�y(t��ng)Ӌ(j��)�Y(ji��)Փ��
�����O(sh��)�@���\(y��n)��(d��ng)�T10��(ch��ng)��ِ�÷�ƽ��ֵ ����10��(ch��ng)��ِ�÷�
����10��(ch��ng)��ِ�÷� ����ݔ����D��ʾ�ij����D�M(j��n)���\(y��n)�㣬��(w��n)ݔ����
����ݔ����D��ʾ�ij����D�M(j��n)���\(y��n)�㣬��(w��n)ݔ���� ��С����٣����f(shu��)��
��С����٣����f(shu��)�� �Ľy(t��ng)Ӌ(j��)�W(xu��)���x��
�Ľy(t��ng)Ӌ(j��)�W(xu��)���x��

��������ļס��҃�λ�\(y��n)��(d��ng)�T��10��(ch��ng)�÷��У����S�C(j��)��ȡһ��(ch��ng)��С��30�ֵĵ÷֣���ĵ÷ִ����ҵĵ÷ֵĸ��ʣ�

����С�}�M��12�֣�
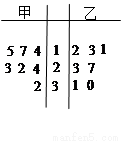
ijِ�����ס��҃����@���\(y��n)��(d��ng)�T��������7��(ch��ng)��ِ���������б�ِ�÷ֵ���r����D��ʾ���o�~�D��ʾ��
������ס��҃����\(y��n)��(d��ng)�T�÷ֵ���λ��(sh��)��
�������J(r��n)����λ�\(y��n)��(d��ng)�T�ijɿ�(j��)����(w��n)����
��������ļס��҃�λ�\(y��n)��(d��ng)�T��7��(ch��ng)�÷��и��S�C(j��)��ȡһ��(ch��ng)�ĵ÷֣���ĵ÷ִ����ҵĵ÷ֵĸ��ʣ�
����С�}�M��12�֣�
ij���S���a(ch��n)�ס��҃ɷN�a(ch��n)Ʒ����֪���a(ch��n)ÿ���ס��҃ɷN�a(ch��n)Ʒ����ú��������ڄ�(d��ng)�����@������(r��n)��ÿ���YԴ���~�����(y��ng)���������ʾ��
|
�YԴ |
�a(ch��n)Ʒ ��ÿ���� |
�Үa(ch��n)Ʒ ��ÿ���� |
�YԴ���~ ��ÿ�죩 |
|
ú��t�� |
9 |
4 |
360 |
|
�����kw��h�� |
4 |
5 |
200 |
|
��������(g��)�� |
3 |
10 |
300 |
|
����(r��n)���f(w��n)Ԫ�� |
7 |
12 |
|
��(w��n)��ÿ�����a(ch��n)�ס��҃ɷN�a(ch��n)Ʒ�����ه����@������(r��n)���~���
��С�}�M��12�֣�
ij���\(y��n)��(d��ng)��(hu��)�ס��҃�������\(y��n)��(d��ng)�T�ɿ�(j��)?n��i)��£?/p>
�ף�9.4��8.7��7.5��8.4��10.1��10.5��10.7��7.2��7.8��10.8��
�ң�9.1��8.7��7.1��9.8��9.7��8. 5��10.1��9.2��10.1��9.1��
��1�����o�~�D��ʾ�ף��҃ɂ�(g��)�ɿ�(j��)��
��2���քeӋ(j��)��ɂ�(g��)�ӱ���ƽ����(sh��)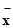 �͘�(bi��o)��(zh��n)��s��������(j��)Ӌ(j��)��Y(ji��)����Ӌ(j��)��λ�\(y��n)��(d��ng)�T�ijɿ�(j��)���^��(w��n)����
�͘�(bi��o)��(zh��n)��s��������(j��)Ӌ(j��)��Y(ji��)����Ӌ(j��)��λ�\(y��n)��(d��ng)�T�ijɿ�(j��)���^��(w��n)����
����С�}�M��12�֣�
ij��˾���a(ch��n)�ס��҃ɷNͰ�b�a(ch��n)Ʒ����֪���a(ch��n)�a(ch��n)Ʒ1Ͱ���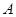 ԭ��1ǧ�ˡ�
ԭ��1ǧ�ˡ�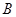 ԭ��2ǧ�ˣ����a(ch��n)�Үa(ch��n)Ʒ1Ͱ���
ԭ��2ǧ�ˣ����a(ch��n)�Үa(ch��n)Ʒ1Ͱ���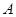 ԭ��2ǧ�ˣ�
ԭ��2ǧ�ˣ�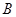 ԭ��1ǧ�ˡ�ÿͰ�a(ch��n)Ʒ������(r��n)��300Ԫ��ÿͰ�Үa(ch��n)Ʒ������(r��n)��400Ԫ����˾�����a(ch��n)�@�ɷN�a(ch��n)Ʒ��Ӌ(j��)���У�Ҫ��ÿ������
ԭ��1ǧ�ˡ�ÿͰ�a(ch��n)Ʒ������(r��n)��300Ԫ��ÿͰ�Үa(ch��n)Ʒ������(r��n)��400Ԫ����˾�����a(ch��n)�@�ɷN�a(ch��n)Ʒ��Ӌ(j��)���У�Ҫ��ÿ������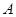 ��
��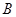 ԭ�϶����ܳ��^(gu��)12ǧ�ˡ���ԓ��˾���Ӱ������a(ch��n)Ӌ(j��)������ʹ��˾�@���������(r��n)��������������(r��n).
ԭ�϶����ܳ��^(gu��)12ǧ�ˡ���ԓ��˾���Ӱ������a(ch��n)Ӌ(j��)������ʹ��˾�@���������(r��n)��������������(r��n).
һ���x���}�������}��10С�}��ÿС�}5�֣���50�֣�
1�D5BADAD 6�D10CBCAA
��������}�������}��6С�}��ÿС�}5�֣���24�֡�
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image257.gif)
17.
�⣺��1�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image259.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image261.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image263.gif)
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image265.gif)
��2����(d��ng)�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image183.gif) �r(sh��)��
�r(sh��)�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image268.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image270.gif)
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image272.gif) ����
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image274.gif) ��
��
��3�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image185.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image277.gif) ����
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image279.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image281.gif)
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image283.gif)
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image285.gif)
18. �⣺��1���ס��҃ɾ��c(di��n)����һ��(g��)ͬ�W(xu��)���Q���c(di��n)���c(di��n)ǡ��2��(g��)A��ͬ�W(xu��)�ЃɷN��r
�� ���Q����A��ͬ�W(xu��)���˕r(sh��)���c(di��n)ǡ��2��(g��)A���ͬ�W(xu��)���¼�ӛ�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image287.gif) .
.
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image289.gif)
�� �ڻ��Q����B��ͬ�W(xu��)���˕r(sh��)���c(di��n)ǡ��2��(g��)A���ͬ�W(xu��)���¼�ӛ�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image291.gif) ..
..
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image293.gif)
���Լ��c(di��n)ǡ��2��(g��)A���ͬ�W(xu��)�ĸ��������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image295.gif) .
.
(2) ���c(di��n)��(n��i)A���ͬ�W(xu��)��(sh��)�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image188.gif) ��
��
�t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image298.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image300.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image302.gif)
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image304.gif) ��
��
19. �⣺��1�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image306.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image308.gif) �r(sh��)��
�r(sh��)�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image310.gif) ȡ����Сֵ
ȡ����Сֵ�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image312.gif) ��
��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image314.gif)
��2���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image316.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image318.gif) ����
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image320.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image322.gif) ����ȥ��
����ȥ��
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image324.gif)
��0,1��
1
��1,2��
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image326.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image328.gif)
0
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image330.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image332.gif)
��
�O��ֵ�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image334.gif)
�p
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image336.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image338.gif) ��(n��i)�����ֵ
��(n��i)�����ֵ�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image334.gif) ��
��
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image341.gif) ��(du��)
��(du��)�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image197.gif) �r(sh��)������ȃr(ji��)��
�r(sh��)������ȃr(ji��)�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image344.gif) �������
�������
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image346.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image348.gif)
20. (1)�C������A��ԭ�c(di��n)��AB,AD,AP����ֱ��������(bi��o)�S����ֱ������(bi��o)ϵ����D��
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image350.jpg)
�t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image352.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image354.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image356.gif)
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image358.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image360.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image362.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image360.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image364.gif)
��2���⣺�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image366.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image203.gif) ��
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image210.gif) �c�����
�c����������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image212.gif) ��,
��, �����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image371.gif)
�^(gu��)E�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image373.gif) �������F���t
�������F���t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image375.gif) ,
,�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image377.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image379.gif) ,����
,���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image381.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image383.gif)
�t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image385.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image387.gif) �c
�c�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image222.gif) ���ɽǵ�����ֵ��
���ɽǵ�����ֵ�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image390.gif) ��
��
��3���O(sh��)�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image392.gif) ƽ��
ƽ�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image224.gif) ���t
���t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image395.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image397.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image399.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image401.gif) �t
�t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image403.gif)
A�c(di��n)��ƽ��PCD�ľ��x�O(sh��)�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image405.gif) ,�t
,�t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image407.gif)
��A�c(di��n)��ƽ��PCD�ľ��x�O(sh��)�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image409.gif) ��
��
21.
�⣺��1���ڵȱȔ�(sh��)�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image228.gif) �У�ǰ
�У�ǰ�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image230.gif) �(xi��ng)�͞�
�(xi��ng)�͞������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image232.gif) ����
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image236.gif) �ɵȲ(sh��)�У��t
�ɵȲ(sh��)�У��t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image234.gif) �ɵȲ(sh��)�С�
�ɵȲ(sh��)�С�
��2����(sh��)�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image228.gif) �����(xi��ng)��
�����(xi��ng)�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image411.gif) �����Ȟ�
�����Ȟ������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image413.gif) �����}��֪��
�����}��֪�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image415.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image417.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image419.gif)
��(d��ng)�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image421.gif) �r(sh��)����
�r(sh��)���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image423.gif)
�@Ȼ�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image425.gif) ���˕r(sh��)�����}��١�
���˕r(sh��)�����}��١�
��(d��ng)�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image427.gif) �r(sh��)����
�r(sh��)���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image429.gif) ��
��
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image431.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image433.gif) ���˕r(sh��)�����}���档
���˕r(sh��)�����}���档
22.
�⣺��1���O(sh��)�E�A���̞������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image435.gif)
�t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image437.gif) ���
��������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image439.gif) ���ԙE�A����
���ԙE�A���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image441.gif)
��2����?y��n)�ֱ�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image243.gif) ƽ����OM������
ƽ����OM�����������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image116.gif) �S�ϵĽؾ���
�S�ϵĽؾ��������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image199.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image446.gif) ������
�����������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image243.gif) �ķ��̞飺
�ķ��̞飺�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image448.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image450.gif)
��?y��n)�ֱ�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image243.gif) �c�E�A����
�c�E�A���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image249.gif) �ɂ�(g��)��ͬ�c(di��n)��
�ɂ�(g��)��ͬ�c(di��n)��
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image453.gif)
���������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image199.gif) ��ȡֵ������
��ȡֵ�����������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image456.gif) ��
��
��3���O(sh��)ֱ�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image252.gif) ��б�ʷքe��
��б�ʷքe�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image459.gif) ��ֻҪ�C��
��ֻҪ�C�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image461.gif) ����
����
�O(sh��)�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image463.gif) ���t
���t�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image465.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image467.gif)
�ɵ������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image469.gif)
�������y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image471.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image473.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image475.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image477.gif)
�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image479.gif)
��ֱ��MA��MB�c�����y(c��)ԇ����?x��n)|������(sh��)�W(xu��)����.files/image054.gif) �Sʼ�K����һ��(g��)���������Ρ�
�Sʼ�K����һ��(g��)���������Ρ�
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com