
題目列表(包括答案和解析)
設甲,乙兩人每次投球命中的概率分別是![]() ,
,![]() ,且兩人各次投球是否命中相互之間沒有影響.
,且兩人各次投球是否命中相互之間沒有影響.
(Ⅰ)若兩人各投球1次,求兩人均沒有命中的概率;
(Ⅱ)若兩人各投球2次,求乙恰好比甲多命中1次的概率.
設甲、乙兩人每次投球命中的概率分別是![]() ,且兩人各次投球是否命中相互之間沒有
,且兩人各次投球是否命中相互之間沒有
影響。
(Ⅰ)若兩人各投球1次,求兩人均沒有命中的概率;
(Ⅱ)若兩人各投球2次,求乙恰好比甲多命中1次的概率。
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
(本小題滿分12分)甲、乙兩人在罰球線投球命中的概率分別為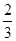 和
和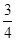 ,假設兩人投球是否命中,相互之間沒有影響;每次投球是否命中,相互之間也沒有影響。
,假設兩人投球是否命中,相互之間沒有影響;每次投球是否命中,相互之間也沒有影響。
(1)甲、乙兩人在罰球線各投球一次,求兩人都沒有命中的概率;
(2)甲、乙兩人在罰球線各投球兩次,求甲投球命中的次數比乙投球命中的次數多的概率。
一、選擇題:本大題共8小題,每小題5分,共40分.
1.B 2.C 3.A 4.A 5.B 6.C 7.D 8.C
二、填空題:本大題共6小題,每小題5分,共30分.
12.24;81 13.1;45° 14.2 |x|
注:兩空的題目,第一個空2分,第二個空3分.
三、解答題:本大題共6小題,共80分.
15.(本小題滿分12分)
(Ⅰ)解:
∵函數f(x)=asinx+bcosx的圖象經過點.files/image054.gif) ,
,
∴.files/image056.gif) 2分 即
2分 即.files/image058.gif) 4分
4分
解得a=1,b=-.files/image060.gif) .
6分
.
6分
(Ⅱ)解:
由(Ⅰ)得f(x)=sinx-.files/image060.gif) cosx=2sin(
cosx=2sin(.files/image062.gif) ).
8分
).
8分
∵0≤x≤π,
∴-.files/image064.gif) 9分
9分
當x-.files/image066.gif) ,即x=
,即x=.files/image068.gif) 時,sin
時,sin.files/image070.gif) 取得最大值1. 11分
取得最大值1. 11分
∴f(x)在[0,π]上的最大值為2,此時x=.files/image068.gif) .
12分
.
12分
16.(本小題滿分13分)
(Ⅰ)解:
記“甲投球命中”為事件A,“乙投球命中”為事件B,則A,B相互獨立,
且P(A)=.files/image018.gif) ,P(B)=
,P(B)=.files/image010.gif) .
.
那么兩人均沒有命中的概率P=P(.files/image075.gif) )=P(
)=P(.files/image077.gif) )P(
)P(.files/image079.gif) )=
)=.files/image081.gif) .
-5分
.
-5分
(Ⅱ)解:
記“乙恰好比甲多命中1次”為事件C,“乙恰好投球命中1次且甲恰好投球命中0次”為事件C1,“乙恰好投球命中2次且甲恰好投球命中1次”為事件C2,則C=C1+C2,C1,C2為互斥事件.
.files/image083.gif) ,
8分
,
8分
.files/image085.gif) ?
?.files/image087.gif) 11分
11分
P(C)=P(C1)+P(C2)=.files/image018.gif) .
13分
.
13分
17.(本小題滿分13分)
解法一:
|