
題目列表(包括答案和解析)
設(shè)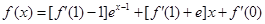
求 及
及 的單調(diào)區(qū)間
的單調(diào)區(qū)間
設(shè)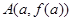 ,
,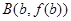
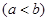 兩點(diǎn)連線的斜率為
兩點(diǎn)連線的斜率為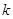 ,問是否存在常數(shù)
,問是否存在常數(shù)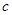 ,且
,且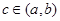 ,當(dāng)
,當(dāng)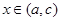 時(shí)有
時(shí)有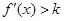 ,當(dāng)
,當(dāng)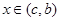 時(shí)有
時(shí)有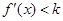 ;若存在,求出
;若存在,求出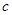 ,并證明之,若不存在說明理由.
,并證明之,若不存在說明理由.
設(shè)
求 及
及 的單調(diào)區(qū)間
的單調(diào)區(qū)間
設(shè) ,
,
 兩點(diǎn)連線的斜率為
兩點(diǎn)連線的斜率為 ,問是否存在常數(shù)
,問是否存在常數(shù) ,且
,且 ,當(dāng)
,當(dāng) 時(shí)有
時(shí)有 ,當(dāng)
,當(dāng) 時(shí)有
時(shí)有 ;若存在,求出
;若存在,求出 ,并證明之,若不存在說明理由.
,并證明之,若不存在說明理由.

 及
及 的單調(diào)區(qū)間
的單調(diào)區(qū)間 ,
,
 兩點(diǎn)連線的斜率為
兩點(diǎn)連線的斜率為 ,問是否存在常數(shù)
,問是否存在常數(shù) ,且
,且 ,當(dāng)
,當(dāng) 時(shí)有
時(shí)有 ,當(dāng)
,當(dāng) 時(shí)有
時(shí)有 ;若存在,求出
;若存在,求出 ,并證明之,若不存在說明理由.
,并證明之,若不存在說明理由.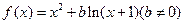
⑴若 ,求
,求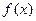 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
⑵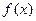 在定義域內(nèi)既有極大值又有極小值
在定義域內(nèi)既有極大值又有極小值 ,求
,求 的取值范圍。
的取值范圍。
已知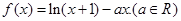
Ⅰ.求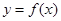 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
Ⅱ.當(dāng)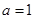 時(shí),求
時(shí),求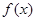 在定義域上的最大值;
在定義域上的最大值;
Ⅰ選擇題
1.C 2. B 3. B 4.B 5.A 6.C 7.A 8.C 9.D 10.A 11.C 12.C
Ⅱ非選擇題
13. 量檢測(cè)-數(shù)學(xué)理.files/image178.gif) 14.
14. 量檢測(cè)-數(shù)學(xué)理.files/image180.gif)
量檢測(cè)-數(shù)學(xué)理.files/image101.gif) 15.
15.量檢測(cè)-數(shù)學(xué)理.files/image182.gif) 16. (2) (3)
16. (2) (3)
17. 解: 量檢測(cè)-數(shù)學(xué)理.files/image184.gif) (4分)
(4分)
(1)增區(qū)間 量檢測(cè)-數(shù)學(xué)理.files/image186.gif) , 減區(qū)間
, 減區(qū)間量檢測(cè)-數(shù)學(xué)理.files/image188.gif) (8分)
(8分)
(2)量檢測(cè)-數(shù)學(xué)理.files/image190.gif) (12分)
(12分)
18.解:因骰子是均勻的,所以骰子各面朝下的可能性相等,設(shè)其中一枚骰子朝下的面上的數(shù)字為量檢測(cè)-數(shù)學(xué)理.files/image170.gif) ,另一枚骰子朝下的面上的數(shù)字為y,則
,另一枚骰子朝下的面上的數(shù)字為y,則量檢測(cè)-數(shù)學(xué)理.files/image193.gif)
量檢測(cè)-數(shù)學(xué)理.files/image132.gif) 的取值如下表:
的取值如下表:
量檢測(cè)-數(shù)學(xué)理.files/image195.gif)
x+y y
量檢測(cè)-數(shù)學(xué)理.files/image196.gif) x
x
1
2
3
5
1
2
3
4
6
2
3
4
5
7
3
4
5
6
8
5
6
7
8
10
從表中可得:量檢測(cè)-數(shù)學(xué)理.files/image198.gif)
量檢測(cè)-數(shù)學(xué)理.files/image200.gif)
量檢測(cè)-數(shù)學(xué)理.files/image202.gif)
量檢測(cè)-數(shù)學(xué)理.files/image204.gif)
⑴ 量檢測(cè)-數(shù)學(xué)理.files/image206.gif)
量檢測(cè)-數(shù)學(xué)理.files/image208.gif) ………………8分
………………8分
⑵量檢測(cè)-數(shù)學(xué)理.files/image132.gif) 的所有可能取值為2,3,4,5,6,7,8,10
的所有可能取值為2,3,4,5,6,7,8,10
量檢測(cè)-數(shù)學(xué)理.files/image132.gif) 的分布列為:
的分布列為:
量檢測(cè)-數(shù)學(xué)理.files/image132.gif)
2
3
4
5
6
7
8
10
P
量檢測(cè)-數(shù)學(xué)理.files/image212.gif)
量檢測(cè)-數(shù)學(xué)理.files/image214.gif)
量檢測(cè)-數(shù)學(xué)理.files/image216.gif)
量檢測(cè)-數(shù)學(xué)理.files/image214.gif)
量檢測(cè)-數(shù)學(xué)理.files/image216.gif)
量檢測(cè)-數(shù)學(xué)理.files/image214.gif)
量檢測(cè)-數(shù)學(xué)理.files/image214.gif)
量檢測(cè)-數(shù)學(xué)理.files/image212.gif)
E量檢測(cè)-數(shù)學(xué)理.files/image132.gif) =2×
=2×量檢測(cè)-數(shù)學(xué)理.files/image212.gif) +3×
+3×量檢測(cè)-數(shù)學(xué)理.files/image214.gif) +4×
+4×量檢測(cè)-數(shù)學(xué)理.files/image216.gif) +5×
+5×量檢測(cè)-數(shù)學(xué)理.files/image214.gif) +6×
+6×量檢測(cè)-數(shù)學(xué)理.files/image216.gif) +7×
+7×量檢測(cè)-數(shù)學(xué)理.files/image214.gif) +8×
+8×量檢測(cè)-數(shù)學(xué)理.files/image214.gif) +10×
+10×量檢測(cè)-數(shù)學(xué)理.files/image212.gif) =5.5………12分
=5.5………12分
19.解:(1)在△CBD中作CO⊥BD. 易證:
CO⊥平面PBD ∴∠CPO即為所求,
∴ 量檢測(cè)-數(shù)學(xué)理.files/image219.gif)
∴ 量檢測(cè)-數(shù)學(xué)理.files/image221.gif) (4分)
(4分)
(2)在△PBC中作EF∥BC交PC于F,
又AD∥BC ∴ AD∥EF ∴ DF⊥PC
又DP=DC ∴ F為PC的中點(diǎn) ∴E為PB的中點(diǎn), ∴ 量檢測(cè)-數(shù)學(xué)理.files/image223.gif) (8分)
(8分)
(3)由(2)得:四邊形ADFE為直角梯形,且 EF=1,DF=量檢測(cè)-數(shù)學(xué)理.files/image225.gif) ,AD=2
,AD=2
∴ 量檢測(cè)-數(shù)學(xué)理.files/image227.gif)
∴ 所求部分體積 量檢測(cè)-數(shù)學(xué)理.files/image229.gif) (12分)
(12分)
20. 解:(1) 量檢測(cè)-數(shù)學(xué)理.files/image231.gif)
令 量檢測(cè)-數(shù)學(xué)理.files/image233.gif)
∴ 增區(qū)間為(0, 1) 減區(qū)間為 量檢測(cè)-數(shù)學(xué)理.files/image235.gif) (4分)
(4分)
(2)函數(shù)量檢測(cè)-數(shù)學(xué)理.files/image055.gif) 圖象如圖所示:
圖象如圖所示:
∴量檢測(cè)-數(shù)學(xué)理.files/image238.gif) 解為:
解為:
① a<0, 0個(gè);
② a=0, a>量檢測(cè)-數(shù)學(xué)理.files/image240.gif) , 1個(gè);
, 1個(gè);
③a=量檢測(cè)-數(shù)學(xué)理.files/image240.gif) , 2個(gè) ; ④ 0<a<
, 2個(gè) ; ④ 0<a<量檢測(cè)-數(shù)學(xué)理.files/image240.gif) , 3個(gè). (8分)
, 3個(gè). (8分)
(3) 量檢測(cè)-數(shù)學(xué)理.files/image242.gif)
∴量檢測(cè)-數(shù)學(xué)理.files/image244.gif) (12分)
(12分)
21.解:(1)由量檢測(cè)-數(shù)學(xué)理.files/image246.gif)
根據(jù)待定系數(shù)法,可得量檢測(cè)-數(shù)學(xué)理.files/image248.gif) .得
.得量檢測(cè)-數(shù)學(xué)理.files/image250.gif) ,
,
故:量檢測(cè)-數(shù)學(xué)理.files/image252.gif) (4分)
(4分)
(2)若量檢測(cè)-數(shù)學(xué)理.files/image148.gif) 為奇數(shù),以下證:
為奇數(shù),以下證:量檢測(cè)-數(shù)學(xué)理.files/image255.gif)
量檢測(cè)-數(shù)學(xué)理.files/image257.gif)
=量檢測(cè)-數(shù)學(xué)理.files/image259.gif)
由于量檢測(cè)-數(shù)學(xué)理.files/image261.gif) ,即
,即量檢測(cè)-數(shù)學(xué)理.files/image263.gif) .
.
①
當(dāng)量檢測(cè)-數(shù)學(xué)理.files/image065.gif) 為偶數(shù)時(shí)
為偶數(shù)時(shí)
量檢測(cè)-數(shù)學(xué)理.files/image266.gif)
量檢測(cè)-數(shù)學(xué)理.files/image268.gif)
②
當(dāng)量檢測(cè)-數(shù)學(xué)理.files/image065.gif) 為奇數(shù)時(shí)
為奇數(shù)時(shí)
量檢測(cè)-數(shù)學(xué)理.files/image270.gif)
=量檢測(cè)-數(shù)學(xué)理.files/image272.gif)
量檢測(cè)-數(shù)學(xué)理.files/image274.gif)
故量檢測(cè)-數(shù)學(xué)理.files/image153.gif) 成立. (12分)
成立. (12分)
22.
解:⑴量檢測(cè)-數(shù)學(xué)理.files/image276.gif)
設(shè)M(量檢測(cè)-數(shù)學(xué)理.files/image278.gif) )且
)且量檢測(cè)-數(shù)學(xué)理.files/image280.gif) ∴
∴量檢測(cè)-數(shù)學(xué)理.files/image282.gif)
化簡(jiǎn): 量檢測(cè)-數(shù)學(xué)理.files/image284.gif) (1分)
(1分)
∴ 量檢測(cè)-數(shù)學(xué)理.files/image286.gif) MN為∠F1 MF2的平分線
MN為∠F1 MF2的平分線
∴ 量檢測(cè)-數(shù)學(xué)理.files/image288.gif)
∴量檢測(cè)-數(shù)學(xué)理.files/image290.gif)
又 量檢測(cè)-數(shù)學(xué)理.files/image292.gif)
量檢測(cè)-數(shù)學(xué)理.files/image294.gif) (6分)
(6分)
⑵量檢測(cè)-數(shù)學(xué)理.files/image296.gif) 代入拋物線
代入拋物線
且量檢測(cè)-數(shù)學(xué)理.files/image298.gif)
量檢測(cè)-數(shù)學(xué)理.files/image300.gif)
量檢測(cè)-數(shù)學(xué)理.files/image302.gif) (9分)
(9分)
又量檢測(cè)-數(shù)學(xué)理.files/image304.gif) ∴
∴量檢測(cè)-數(shù)學(xué)理.files/image306.gif)
量檢測(cè)-數(shù)學(xué)理.files/image308.gif)
①當(dāng)量檢測(cè)-數(shù)學(xué)理.files/image310.gif) 時(shí),不等式成立
時(shí),不等式成立
②當(dāng)量檢測(cè)-數(shù)學(xué)理.files/image312.gif)
量檢測(cè)-數(shù)學(xué)理.files/image314.gif)
∴量檢測(cè)-數(shù)學(xué)理.files/image176.gif) 的取值范圍為:
的取值范圍為: 量檢測(cè)-數(shù)學(xué)理.files/image317.gif) (14分)
(14分)
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com