
題目列表(包括答案和解析)
已知![]() 均為正數(shù),
均為正數(shù),![]() ,則
,則![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷 (非選擇題 共90分)
二、填空題:本大題共4小題,每小題4分,共16分,將答案填在題中的橫線上。
第Ⅱ卷(非選擇題,共90分)
二、填空題:(本大題4小題,每小題5分,滿分20分)
13.用一個(gè)平面去截正方體,其截面是一個(gè)多邊形,則這個(gè)多邊形的邊數(shù)最多是 條 。
已知函數(shù)
(1)在給定的直角坐標(biāo)系內(nèi)畫(huà)出![]() 的圖象;
的圖象;
(2)寫(xiě)出![]() 的單調(diào)遞增區(qū)間(不需要證明);
的單調(diào)遞增區(qū)間(不需要證明);
(3)寫(xiě)出![]() 的最大值和最小值(不需要證明).
的最大值和最小值(不需要證明).
(第II卷) 50分
一、填空題(本大題共2小題,每小題4分,共8分.把答案填在答題卡上)
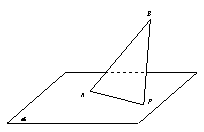 如圖
如圖![]() 是長(zhǎng)度為定值的平面
是長(zhǎng)度為定值的平面![]() 的斜線段,點(diǎn)
的斜線段,點(diǎn)![]() 為斜足,若點(diǎn)
為斜足,若點(diǎn)![]() 在平面
在平面![]() 內(nèi)運(yùn)動(dòng),使得
內(nèi)運(yùn)動(dòng),使得![]() 的面積為定值,則動(dòng)點(diǎn)P的軌跡是
的面積為定值,則動(dòng)點(diǎn)P的軌跡是
A.圓 B.橢圓
C一條直線 D兩條平行線
第Ⅱ卷(非選擇題 共110分)
填空題(本大題共6小題,每小題5分,共30分.)
等差數(shù)列![]() 中,
中,![]() ,若數(shù)列
,若數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,則
,則![]() 的值為
的值為
A、18 B、16 C、15 D、14
第Ⅱ卷(非選擇題 共90分)
二. 填空題:本大題共4小題,每小題4分,共16分,把答案填在題中橫線上.
一.選擇題(本大題共12小題,每小題5分,共60分.)
D C B B C D C A C C A B
二.填空題(本大題共4小題,每小題4分,共16分.)
(13)學(xué)文.files/image241.gif) (14)
(14)學(xué)文.files/image243.gif) (15)
(15)學(xué)文.files/image245.gif) (16)―1
(16)―1
三.解答題
(17)(本小題滿分12分)
解:(Ⅰ)將一顆骰子先后拋擲2次,此問(wèn)題中含有36個(gè)等可能的基本事件. 2分
記“兩數(shù)之和為
∴ P(A)學(xué)文.files/image247.gif) .
.
記“兩數(shù)之和是4的倍數(shù)”為事件B,則事件B中含有9個(gè)基本事件,
∴ P(B)學(xué)文.files/image249.gif) .
.
∵ 事件A與事件B是互斥事件,∴ 所求概率為 學(xué)文.files/image251.gif) . 8分
. 8分
學(xué)文.files/image252.gif) (Ⅱ)記“點(diǎn)(x,y)在圓
(Ⅱ)記“點(diǎn)(x,y)在圓 學(xué)文.files/image171.gif) 的內(nèi)部”事件C,則事件C中共含有11個(gè)基本事件,∴ P(C)=
的內(nèi)部”事件C,則事件C中共含有11個(gè)基本事件,∴ P(C)=學(xué)文.files/image254.gif) . 12分
. 12分
(18)(本小題滿分12分)
解:(Ⅰ)∵ ABC―A1B
∴ BB1⊥AC,BP⊥AC.∴ AC ⊥ 平面PBB1.
又∵M(jìn)、N分別是AA1、CC1的中點(diǎn),
∴ MN∥AC.∴ MN ⊥ 平面PBB1 . 4分
(Ⅱ)∵M(jìn)N∥AC,∴A C ∥ 平面MNQ.
QN是△B1CC1的中位線,∴B
∴平面AB
(Ⅲ)由題意,△MNP的面積學(xué)文.files/image256.gif) .
.
Q點(diǎn)到平面ACC
∴ 學(xué)文.files/image258.gif) .∴三棱錐 Q ― MNP 的體積
.∴三棱錐 Q ― MNP 的體積學(xué)文.files/image260.gif) . 12分
. 12分
(19)(本小題滿分12分)
解:(Ⅰ):學(xué)文.files/image262.gif)
學(xué)文.files/image264.gif)
學(xué)文.files/image266.gif) . 3分
. 3分
依題意,學(xué)文.files/image186.gif) 的周期
的周期學(xué)文.files/image269.gif) ,且
,且學(xué)文.files/image176.gif) ,∴
,∴ 學(xué)文.files/image272.gif) .∴
.∴學(xué)文.files/image274.gif) .
.
∴ 學(xué)文.files/image276.gif) . 5分
. 5分
∵ 學(xué)文.files/image044.gif)
學(xué)文.files/image279.gif) [0,
[0,學(xué)文.files/image281.gif) ], ∴
], ∴ 學(xué)文.files/image283.gif) ≤
≤學(xué)文.files/image285.gif) ≤
≤學(xué)文.files/image287.gif) ,∴
,∴ 學(xué)文.files/image104.gif) ≤
≤學(xué)文.files/image290.gif) ≤1,
≤1,
∴ 學(xué)文.files/image186.gif) 的最小值為
的最小值為 學(xué)文.files/image293.gif) ,即
,即 學(xué)文.files/image295.gif) ∴
∴
學(xué)文.files/image297.gif) .
.
∴ 學(xué)文.files/image299.gif) . 7分
. 7分
(Ⅱ)∵ 學(xué)文.files/image301.gif) =2
=2學(xué)文.files/image303.gif)
學(xué)文.files/image305.gif) , ∴
, ∴ 學(xué)文.files/image307.gif) .
.
又 ∵ ∠學(xué)文.files/image309.gif) ∈(0,
∈(0,學(xué)文.files/image281.gif) ), ∴ ∠
), ∴ ∠學(xué)文.files/image309.gif) =
=學(xué)文.files/image312.gif) . 9分
. 9分
在學(xué)文.files/image314.gif) △ABC中,∵
△ABC中,∵ 學(xué)文.files/image316.gif) ,
,學(xué)文.files/image197.gif) ,
,
∴ 學(xué)文.files/image318.gif) ,
,學(xué)文.files/image320.gif) .解得
.解得 學(xué)文.files/image199.gif)
學(xué)文.files/image323.gif)
學(xué)文.files/image325.gif) .
.
又 ∵ 0學(xué)文.files/image327.gif) , ∴
, ∴ 學(xué)文.files/image329.gif)
學(xué)文.files/image331.gif) . 12分
. 12分
(20)(本小題滿分12分)
解:(Ⅰ)對(duì)學(xué)文.files/image186.gif) 求導(dǎo)得
求導(dǎo)得 學(xué)文.files/image333.gif) .
.
依題意有 學(xué)文.files/image335.gif) ,且
,且 學(xué)文.files/image337.gif) .∴
.∴ 學(xué)文.files/image339.gif) ,且
,且 學(xué)文.files/image341.gif) .
.
解得 學(xué)文.files/image343.gif) . ∴
. ∴ 學(xué)文.files/image345.gif) . 6分
. 6分
(Ⅱ)由上問(wèn)知學(xué)文.files/image347.gif) ,令
,令學(xué)文.files/image349.gif) ,得
,得 學(xué)文.files/image351.gif) .
.
顯然,當(dāng) 學(xué)文.files/image353.gif) 或
或 學(xué)文.files/image355.gif) 時(shí),
時(shí),學(xué)文.files/image357.gif) ;當(dāng)
;當(dāng) 學(xué)文.files/image359.gif) 時(shí),
時(shí),
學(xué)文.files/image361.gif) .∴ 函數(shù)
.∴ 函數(shù)學(xué)文.files/image186.gif) 在
在學(xué)文.files/image363.gif) 和
和學(xué)文.files/image365.gif) 上是單調(diào)遞增函數(shù),在
上是單調(diào)遞增函數(shù),在學(xué)文.files/image367.gif) 上是單調(diào)遞減函數(shù).
上是單調(diào)遞減函數(shù).
∴學(xué)文.files/image186.gif) 當(dāng)
當(dāng)學(xué)文.files/image369.gif) 時(shí)取極大值,極大值是
時(shí)取極大值,極大值是學(xué)文.files/image371.gif) .
.
學(xué)文.files/image186.gif) 當(dāng)
當(dāng)學(xué)文.files/image373.gif) 時(shí)取極小值,極小值是
時(shí)取極小值,極小值是學(xué)文.files/image375.gif) . 12分
. 12分
學(xué)文.files/image376.gif) (21)(本小題滿分12分)
(21)(本小題滿分12分)
解:(Ⅰ)∵ 學(xué)文.files/image378.gif) ,
,
∴學(xué)文.files/image380.gif) .
.
設(shè)O關(guān)于直線 學(xué)文.files/image212.gif) 的
的
對(duì)稱點(diǎn)為學(xué)文.files/image383.gif) 的橫坐標(biāo)為
的橫坐標(biāo)為 學(xué)文.files/image385.gif) .
.
又易知直線學(xué)文.files/image387.gif) 解得線段
解得線段學(xué)文.files/image389.gif) 的中點(diǎn)坐標(biāo)
的中點(diǎn)坐標(biāo)
為(1,-3).∴學(xué)文.files/image391.gif) .
.
∴ 橢圓方程為 學(xué)文.files/image393.gif) . 5分
. 5分
(Ⅱ)顯然直線AN存在斜率,設(shè)直線AN的方程為 學(xué)文.files/image395.gif) ,代入
,代入 學(xué)文.files/image393.gif) 并整理得:
并整理得:學(xué)文.files/image397.gif) .
.
設(shè)點(diǎn)學(xué)文.files/image399.gif) ,
,學(xué)文.files/image401.gif) ,則
,則學(xué)文.files/image403.gif) .
.
由韋達(dá)定理得 學(xué)文.files/image405.gif) ,
,學(xué)文.files/image407.gif) . 8分
. 8分
∵ 直線ME方程為 學(xué)文.files/image409.gif) ,令
,令學(xué)文.files/image411.gif) ,得直線ME與x軸的交點(diǎn)
,得直線ME與x軸的交點(diǎn)
的橫坐標(biāo) 學(xué)文.files/image413.gif) .
.
將學(xué)文.files/image415.gif) ,
,學(xué)文.files/image417.gif) 代入,并整理得
代入,并整理得 學(xué)文.files/image419.gif) . 10分
. 10分
再將韋達(dá)定理的結(jié)果代入,并整理可得學(xué)文.files/image421.gif) .
.
∴ 直線ME與學(xué)文.files/image044.gif) 軸相交于定點(diǎn)(
軸相交于定點(diǎn)(學(xué)文.files/image108.gif) ,0). 12分
,0). 12分
(22)(本小題滿分14分)
證明:(Ⅰ)∵
學(xué)文.files/image229.gif) , ∴
, ∴ 學(xué)文.files/image426.gif) .
.
顯然
學(xué)文.files/image428.gif) , ∴
, ∴ 學(xué)文.files/image430.gif) . 5分
. 5分
∴
學(xué)文.files/image432.gif) ,
,學(xué)文.files/image434.gif) ,……,
,……,學(xué)文.files/image430.gif) ,
,
將這學(xué)文.files/image437.gif) 個(gè)等式相加,得
個(gè)等式相加,得 學(xué)文.files/image439.gif) ,∴
,∴ 學(xué)文.files/image235.gif) .
7分
.
7分
(Ⅱ)∵
學(xué)文.files/image237.gif) ,∴
,∴ 學(xué)文.files/image443.gif) . 9分
. 9分
∴
學(xué)文.files/image445.gif) .即
.即 學(xué)文.files/image447.gif) . 11分
. 11分
∴
學(xué)文.files/image449.gif) ,即
,即
學(xué)文.files/image239.gif) . 14分
. 14分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com