
題目列表(包括答案和解析)
 A.(選修4-4坐標系與參數方程)已知點A是曲線ρ=2sinθ上任意一點,則點A到直線ρsin(θ+
A.(選修4-4坐標系與參數方程)已知點A是曲線ρ=2sinθ上任意一點,則點A到直線ρsin(θ+| π | 3 |
 A.(不等式選做題)若關于x的不等式|x+3|-|x+2|≥log2a有解,則實數a的取值范圍是:
A.(不等式選做題)若關于x的不等式|x+3|-|x+2|≥log2a有解,則實數a的取值范圍是:| PB |
| PA |
| 1 |
| 2 |
| PC |
| PD |
| 1 |
| 3 |
| BC |
| AD |
|
| 2 |
| cosθ-sinθ |
| 2 |
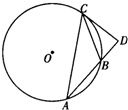 A.(不等式選做題)
A.(不等式選做題)| 3 |
| π |
| 3 |
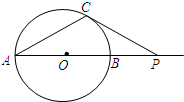 A.不等式
A.不等式| x-2 |
| x2+3x+2 |
| 3 |
|
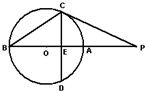 A.(不等式選做題)不等式|3x-6|-|x-4|>2x的解集為
A.(不等式選做題)不等式|3x-6|-|x-4|>2x的解集為| π |
| 4 |
| 2 |
一、選擇題:
1.解析:B.由 且
且 能夠推出
能夠推出 ;反之,由
;反之,由 只能推出
只能推出 或
或 ,而不能推出
,而不能推出 且
且 .故“
.故“ ”是“
”是“ 且
且 ”的必要不充分條件,故選B.
”的必要不充分條件,故選B.
評析:有關充要條件的判定問題,概念性較強,進行判斷時,必須緊扣概念.一方面,要正確理解充要條件本身的概念,進行雙向推理,準確判斷;另一方面,還要注意根據具體問題所涉及到的數學概念來思考.本題中,弄清并集和交集概念中“或”與“且”的關系顯得很重要.
2.解析:B.∵△= .要使函數
.要使函數 的一個零點在
的一個零點在 內,必須滿足條件:
內,必須滿足條件: ,即
,即 ,
,
∴ ,∴實數k的取值范圍為(2,3).
,∴實數k的取值范圍為(2,3).
3.解析:D.化簡復數 可得
可得 ,∴
,∴ ,
,
故選D.
4.解析:B 先作出直線A1B與平面BC1D1所成角,再通過解三角形求出其正切值.如圖,連結 交
交 于
于 ,連結
,連結 .由
.由 ,
, ,又
,又 ,得
,得 ,所以
,所以 就是直線A1B與平面BC1D1所成角.在直角
就是直線A1B與平面BC1D1所成角.在直角 中,求得
中,求得 ,故選B.
,故選B.
評析:平面的斜線與平面所成的角,就是這條斜線與它在該平面上
 的射影所成的銳角,根據題目的條件作出斜線在該平面上的射影
的射影所成的銳角,根據題目的條件作出斜線在該平面上的射影
是實現解題的關鍵,而作射影的關鍵則是作出平面的垂線,要注
意面面垂直的性質在作平面的垂線時的應用.
5.解析:
A.特值法.取B=0,A=1,C=-1,則M(1, ),
),
N(1,- ), ∴
), ∴ = x1x2+y1y2 =-2.故選A .
= x1x2+y1y2 =-2.故選A .
6.解析
B.設點 是函數
是函數 上的任意一點,點
上的任意一點,點 關于點
關于點 的對稱點為
的對稱點為 ,則
,則 由
由 在
在 上,
上,
得 ,∴
,∴ ,即
,即 .故選B.
.故選B.
7.解析: C.圖象法.由 的圖象可得,
的圖象可得, 在
在 上是增函數,在
上是增函數,在 上是減函數,又
上是減函數,又 是偶函數,∴
是偶函數,∴ ,
,
∴ ,解得
,解得 .故選C.
.故選C.
8.解析:B,由 ,得:
,得: ,即
,即 ,
,
解之得 ,由于
,由于 ,故
,故 ;選B
;選B
9.解析: B.如果四塊均不同色,則有 種涂法;如果有且僅有兩塊同色,它們必是相對的兩塊,有
種涂法;如果有且僅有兩塊同色,它們必是相對的兩塊,有 種涂法;如果兩組相對的兩塊分別同色,則有
種涂法;如果兩組相對的兩塊分別同色,則有 種涂法.根據分類計數原理,得到涂色方法種數為
種涂法.根據分類計數原理,得到涂色方法種數為 (種),故選B.
(種),故選B.
10.解析:選D.①②③易于判斷其真。 .
.
 ,即曲線上任一點P(x,y)在單位圖
,即曲線上任一點P(x,y)在單位圖 外,(點(±1,0)在圓上),
外,(點(±1,0)在圓上),
則S>π?12=π
評析:f(x,y)=f(x,-y) 曲線f(x,y)=0,關于x軸對稱;
曲線f(x,y)=0,關于x軸對稱;
f(x,y)=f(-x, y) 曲線f(x,y)=0,關于y軸對稱;
曲線f(x,y)=0,關于y軸對稱;
f(x,y)=f(-x, -y) 曲線f(x,y)=0,關于原點對稱。
曲線f(x,y)=0,關于原點對稱。
 11.解析:D,在EF上任意取一點M,直線
11.解析:D,在EF上任意取一點M,直線 與M確定一個平面,
與M確定一個平面,
這個平面與CD有且僅有1個交點N, 當M取不同的位置就確
定不同的平面,從而與CD有不同的交點N,而直線MN與這
3條異面直線都有交點的.如右圖:
評析:本題主要考查立體幾何中空間直線相交問題,考查學生
的空間想象能力。
12.解析:C.P(X=8)= ,P(X=7)=
,P(X=7)= ,
,
P(X=6)= , 所以P(X≥6)=
, 所以P(X≥6)= ,
,
即線路信息暢通的概率為 ,故選C.
,故選C.
二、填空題:
13.解析: .由
.由 ,得
,得 ,即
,即 ,又由
,又由 ,得
,得 ,∴
,∴ ,
,
于是,

 .
.
14. 解析: .如圖,
.如圖, 過點
過點 ,
, .
.
 在點
在點 處取得最小值,
處取得最小值, 點在直線
點在直線
 上,
上, ,∴
,∴ .
.
評析:簡單的線性規劃問題,其約束條件是平面上的一個
多邊形閉區域,或者是向某一方向無限延展的半閉區域,而目標函數一般在邊界的頂點處取得最值.解題時通常運用圖解法,根據題意畫出圖形,從圖形中尋求思路、獲得答案,體現了數形結合的思想方法.
15.解析:f(x)=x2+2x+1 .設f(x)=ax2+bx+c
(a≠0),則△=b2-
∴ ,故 f(x)=x2+2x+1 .
,故 f(x)=x2+2x+1 .
16.解析:橢圓 與雙曲線
與雙曲線 的焦距相等.由橢圓
的焦距相等.由橢圓 與雙曲線
與雙曲線 的焦距相等,分析橢圓和雙曲線的標準方程中參數之間的關系,運用類比推理的方法,不難得到推廣后的一個命題為:橢圓
的焦距相等,分析橢圓和雙曲線的標準方程中參數之間的關系,運用類比推理的方法,不難得到推廣后的一個命題為:橢圓 與雙曲線
與雙曲線 的焦距相等.
的焦距相等.
評析:推廣命題有多種方法,其中類比推理是一種常用方法.值得指出的是,本題的答案不唯一,例如,我們還可以得到推廣后的更具一般性的命題:橢圓 與雙曲線
與雙曲線
 的焦距相等.
的焦距相等.
三、解答題:
17.解析:(Ⅰ) ,在
,在 中,由余弦定理,
中,由余弦定理,
得 ,
,
∴ ,
,
 (2分)
(2分)
由 ,
, ,
,
由 得,
得, ,
,
∴ ,從而
,從而
 (4分)
(4分)
由題意可知 ,∴
,∴ ,
,
 (5分)
(5分)
又∵△BCD是 ,∴
,∴ 當
當 時,則
時,則 ,由
,由 ,
,
∴ ;
;
 當
當 時,則
時,則 ,由
,由 ,∴
,∴ ;
;
綜上, .
.
 (7分)
(7分)
(Ⅱ)由(1)知 ,∴向量
,∴向量 與
與 的夾角為
的夾角為 ,
,  (9分)
(9分)
 當
當 時,
時, ,
, ,
,
∴ .
.
 (10分)
(10分)
 當
當 時,
時, ,
, ,
,
∴ .
.
 (12分)
(12分)
評析:本題考查平面向量和解三角形的基礎知識,考查分類討論的思想方法.求解時容易發生的錯誤是:(1)將條件“△BCD是直角三形”當作“△BCD是以角 是直角三形”來解,忽略對
是直角三形”來解,忽略對 為直角的情況的討論;(2)在計算
為直角的情況的討論;(2)在計算 時,將
時,將 當作向量
當作向量 與
與 的夾角,忽略了確定兩個向量的夾角時必須將它們的起點移到一起.暴露出思維的不嚴謹和概念理解的缺陷,在復習中要引起重視,加強訓練.
的夾角,忽略了確定兩個向量的夾角時必須將它們的起點移到一起.暴露出思維的不嚴謹和概念理解的缺陷,在復習中要引起重視,加強訓練.
18.解析: (Ⅰ)做了三次實驗,至少兩次實驗成功的情形有兩種:
(1)恰有兩次成功,其概率為 ;
;
 (2分)
(2分)
(2)三次都成功,其概率為 .
.
 (4分)
(4分)
故得所求之概率為 .
.  (6分)
(6分)
(Ⅱ)在第4次成功之前,共做了6次試驗,其中三次成功、三次失敗,且恰有兩次連續失敗,其各種可能情況的種數為 .
.
 (10分)
(10分)
因此,所求之概率為 .
.
 (12分)
(12分)
19.解析:(Ⅰ)∵SB=SC,AB=AC,M為BC中點,
∴SM⊥BC,AM⊥BC.  (2分)
(2分)
由棱錐的側面積等于底面積的2倍,即

得 .
.
 (4分)
(4分)
(Ⅱ)作正三棱錐的高SG,則G為正三角形ABC的中心,G在AM上,
∵SM⊥BC,AM⊥BC,
∴∠SMA是二面角S―BC―A的平面角. (6分)
(6分)
在Rt△SGM中,∵ ∴∠SMA=∠SMG=60°,
∴∠SMA=∠SMG=60°,
即二面角S―BC―A的大小為60°.  (8分)
(8分)
(Ⅲ)∵△ABC的邊長是3,
∴ ,
,  (10分)
(10分)
∴ .
.  (12分)
(12分)
評析計算二面角大小,既可以根據二面角的定義,通過作出二面角的平面角,再解三角形求角,也可以運用向量方法,轉化為計算兩個平面的法向量的夾角.做題時要考慮前后聯系,注意選擇簡便的方法.
20.解析:(Ⅰ)證明:假設存在一個實數,使{an}是等比數列,則有 ,即
,即
( )2=
)2= 2
2 矛盾.
矛盾.
所以{an}不是等比數列.
 (3分)
(3分)
(Ⅱ)證明:∵


 又
又 由上式知
由上式知
 故當
故當 數列{bn}是以
數列{bn}是以 為首項,
為首項, 為公比的等比數列.
為公比的等比數列.
 (7分)
(7分)
(Ⅲ)當 由(Ⅱ)得
由(Ⅱ)得 于是
于是
 當
當 時,
時, ,從而
,從而 上式仍成立.
上式仍成立.
要使對任意正整數n , 都有
即
 (9分)
(9分)
令
當n為正奇數時, 當n為正偶數時,
當n為正偶數時,
 于是可得
于是可得
綜上所述,存在實數 ,使得對任意正整數
,使得對任意正整數 ,都有
,都有
 的取值范圍為
的取值范圍為
 (12分)
(12分)
評析:(1)求解等差數列與等比數列的有關問題,定義、公式和性質是主要工具,要注意抓住基本量───首項和公差(公比),方程思想、化歸思想和運算能力是考查的重點;(2)正面求解,直接證明難以突破時,可以考慮從反面入手,運用正難則反的思想來處理,反證法就是從反面入手的一種重要的推理方法,一般地,以否定的形式出現的數學命題,我們常用反證法來實現證明。
21.解析:(Ⅰ) ,……(1分)
,……(1分)
∵函數 在
在 上單調遞增,在
上單調遞增,在 上單調遞減,
上單調遞減,
∴ 在
在 處取得極大值,有
處取得極大值,有 ,
,
 (3分)
(3分)
即 ,這就是所求的
,這就是所求的 之間的關系式.
之間的關系式.  (4分)
(4分)
(Ⅱ)當 在
在 處取得極小值,有
處取得極小值,有 ,即
,即 ,
①
,
①
又由(Ⅰ)有: ②聯立①和②,解得
②聯立①和②,解得 .
.
 (5分)
(5分)
此時, ,在
,在 上
上 ,
,
在 上
上 ,
,
∴ 在
在 處確可取得極小值,故
處確可取得極小值,故 ,
,  (7分)
(7分)
從而 .
.
 (8分)
(8分)
(Ⅲ)由(Ⅰ)得: ,
,
∴ ,
,
它在 上為減函數,在
上為減函數,在 為增函數.
為增函數.  (10分)
(10分)
若存在實數 ,使
,使 在
在 上為單調函數,則有
上為單調函數,則有 ,得
,得 .又因為
.又因為 ,有
,有 ,這與
,這與 矛盾.
矛盾.
所以滿足題意的實數 不存在.
不存在.
 (12分)
(12分)
評析: 導數是研究函數性質的一個有力工具,運用導數求函數的單調區間和極值,可轉化為解不等式 和方程
和方程 ,顯得非常簡捷且易于操作.值得注意的是:
,顯得非常簡捷且易于操作.值得注意的是: 是
是 取得極值的必要條件,因此,在(Ⅱ)中,由
取得極值的必要條件,因此,在(Ⅱ)中,由 求出
求出 ,必須檢驗.
,必須檢驗.
22.解析:(Ⅰ)由題意可得 ,
,  (2分)
(2分)
由 ,得
,得 ,∴
,∴ ,
,  (4分)
(4分)
∴橢圓 的方程為
的方程為 .
.
 (4分)
(4分)
(Ⅱ)由(Ⅰ)可得橢圓 的左焦點為
的左焦點為 ,左準線為
,左準線為 ,
,
連結 ,則
,則 ,設
,設 ,則
,則 ,
,
∴ ,
,
 (6分)
(6分)
化簡得 的方程為
的方程為 .
.
 (8分)
(8分)
(Ⅲ)將曲線 向右平移2個單位,得曲線
向右平移2個單位,得曲線 的方程為:
的方程為:  ,其焦點為
,其焦點為 ,準線為
,準線為 ,對稱軸為
,對稱軸為 軸.
軸.  (10分)
(10分)
設直線 的方程為
的方程為 ,代入y2=4x,得y2-4ty-4=0.
,代入y2=4x,得y2-4ty-4=0.
由題意,可設 (
( ),
), (
( ),則y1y2=-4,
),則y1y2=-4,
且有
 (12分)
(12分)
∴ ,
, ,
,
得 .
.
∴ 三點共線.
三點共線.
 (14分)
(14分)
評析:證明三點共線的方法很多,這里運用向量共線定理來證,體現了平面向量與解析幾何知識的交匯和平面向量知識在解析幾何中的應用.近幾年的高考突出了在知識網絡的交匯點處設計命題的要求,平面向量與解析幾何知識的綜合考查成為一個不衰的熱點,復習中要引起重視.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com