
題目列表(包括答案和解析)
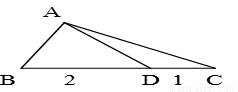
△ABC中,D在邊BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的長及△ABC的面積。
【解析】本試題主要考查了余弦定理的運用。利用由題意得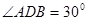 ,
,

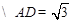 ,
,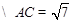 并且
并且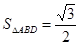 有
有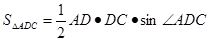 得到結論。
得到結論。
解:(Ⅰ)由題意得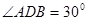 ,
,
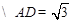 ………1分
………1分 …………1分
…………1分
(Ⅱ)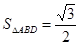 ………………1分
………………1分
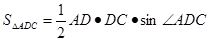
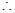
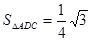

在△ABC中,內角A、B、C所對邊的邊長分別是a、b、c,已知c=2,C= .
.
(Ⅰ)若△ABC的面積等于 ,求a、b;
,求a、b;
(Ⅱ)若 ,求△ABC的面積.
,求△ABC的面積.
【解析】第一問中利用余弦定理及已知條件得 又因為△ABC的面積等于
又因為△ABC的面積等于 ,所以
,所以 ,得
,得 聯(lián)立方程,解方程組得
聯(lián)立方程,解方程組得 .
.
第二問中。由于 即為即
即為即 .
.
當 時,
時,
 ,
,  ,
,  ,
,
 所以
所以 當
當 時,得
時,得 ,由正弦定理得
,由正弦定理得 ,聯(lián)立方程組
,聯(lián)立方程組 ,解得
,解得 ,得到
,得到 。
。
解:(Ⅰ) (Ⅰ)由余弦定理及已知條件得 ,………1分
,………1分
又因為△ABC的面積等于 ,所以
,所以 ,得
,得 ,………1分
,………1分
聯(lián)立方程,解方程組得 .
……………2分
.
……………2分
(Ⅱ)由題意得
 ,
,
即 .
…………2分
.
…………2分
當 時,
時,
 ,
,  ,
,  ,
,
 ……1分
……1分
所以 ………………1分
………………1分
當 時,得
時,得 ,由正弦定理得
,由正弦定理得 ,聯(lián)立方程組
,聯(lián)立方程組
 ,解得
,解得 ,
, ;
所以
;
所以
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| r1 |
| 1 |
| r2 |
| b2 |
| a-ccosθ |
| b2 |
| a-ccos(π-θ) |
| b2 |
| a+ccosθ |
| 1 |
| r |
| 1 |
| r |
| 2a |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
在△ABC中, 為三個內角
為三個內角 為三條邊,
為三條邊, 且
且
(I)判斷△ABC的形狀;
(II)若 ,求
,求 的取值范圍.
的取值范圍.
【解析】本題主要考查正余弦定理及向量運算
第一問利用正弦定理可知,邊化為角得到

所以得到B=2C,然后利用內角和定理得到三角形的形狀。
第二問中,

得到。
(1)解:由 及正弦定理有:
及正弦定理有:
∴B=2C,或B+2C ,若B=2C,且
,若B=2C,且 ,∴
,∴ ,
, ;∴B+2C
;∴B+2C ,則A=C,∴
,則A=C,∴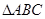 是等腰三角形。
是等腰三角形。
(2)

國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com