題目列表(包括答案和解析)
記數列{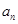
}的前n項和為為
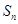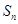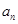，且＋＋n＝0（n∈N*）恒成立．
（1）求證：數列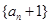
是等比數列；
（2）已知2是函數f（x）＝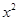
＋ax－1的零點，若關于x的不等式f（x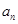）≥對任意n∈N﹡在x∈（－∞，λ]上恒成立，求實常數λ的取值范圍．
記數列{
}的前n項和為為
，且＋＋n＝0（n∈N*）恒成立．
（1）求證：數列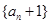
是等比數列；
（2）已知2是函數f（x）＝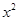
＋ax－1的零點，若關于x的不等式f（x）≥對任意n∈N﹡在x∈（－∞，λ]上恒成立，求實常數λ的取值范圍．
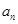}的前n項和為為
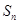，且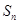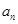＋＋n＝0（n∈N*）恒成立．
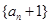是等比數列；
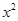＋ax－1的零點，若關于x的不等式f（x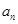）≥對任意n∈N﹡在x∈（－∞，λ]上恒成立，求實常數λ的取值范圍．數列
的前n項和記為
，
（1）t為何值時，數列是等比數列？
（2）在（1）的條件下，若等差數列
的前n項和
有最大值，且
，又
成等比數列，求。
數列
的前n項和記為
,
,點
在直線
上,n∈N*．
（1）求證：數列是等比數列，并求數列的通項公式
；
（2）設
,
是數列
的前n項和,求
的值．
1-10．CDBBA CACBD
11．
12. ①③④ 13.-2或1 14. 
、
15.2 16. 
17.
.
18．
解：（1）由已知
7分
（2）由
10分
由余弦定理得
14分
19.（1）證明：∵PA⊥底面ABCD，BC
平面AC，∴PA⊥BC, 3分
∵∠ACB=90°，∴BC⊥AC，又PA∩AC=A，∴BC⊥平面PAC. 5分
（2）解：過C作CE⊥AB于E，連接PE，
∵PA⊥底面ABCD，∴CE⊥面PAB，
∴直線PC與平面PAB所成的角為
， 10分
∵AD=CD=1，∠ADC=60°，∴AC=1，PC=2,
中求得CE=
，∴
. 14分
20．解：（1）由
①，得
②，
②-①得：
. 4分
（2）由
求得
. 7分
∴
，
11分
∴
.
14分
21．解：
（1）由
得c=1 1分
， 4分
5分
得
，
時取得極值.由
，
得
∴
. 8分
，
，∴當
時，
， 
在
上遞減. 12分
∴函數
的零點有且僅有1個 15分
，由已知
，
， 2分
，
6分
點 B（0，t），點
， 7分
， 9分
，
，
，
， 13分
，又
時，
，
面積的最小值為
15分