
題目列表(包括答案和解析)
(本小題滿分14分)
.已知中心在原點的橢圓的一個焦點為(0 ,![]() ),且過點
),且過點![]() ,過A作傾斜角互補的兩條直線,它們與橢圓的另一個交點分別為點B和點C。
,過A作傾斜角互補的兩條直線,它們與橢圓的另一個交點分別為點B和點C。
(1)求橢圓的標準方程;
(2)求證:直線BC的斜率為定值,并求這個定值。
(3)求三角形ABC面積的最大值。
(本小題滿分14分)
已知直線l與橢圓![]() (a>b>0)相交于不同兩點A、B,
(a>b>0)相交于不同兩點A、B,![]() ,且
,且![]() ,以M為焦點,以橢圓的右準線為相應準線的雙曲線與直線l相交于N(4,
,以M為焦點,以橢圓的右準線為相應準線的雙曲線與直線l相交于N(4,![]() 1). (I)求橢圓的離心率
1). (I)求橢圓的離心率![]() ; (II)設雙曲線的離心率為
; (II)設雙曲線的離心率為![]() ,記
,記![]() ,求
,求![]() 的解析式,并求其定義域和值域.
的解析式,并求其定義域和值域.
(本小題滿分14分)已知定義在 上的函數
上的函數 ,滿足條件:①
,滿足條件:①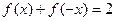 ,②對非零實數
,②對非零實數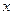 ,都有
,都有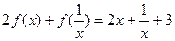 .
.
(1)求函數 的解析式;
的解析式;
(2)設函數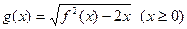 ,直線
,直線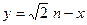 分別與函數
分別與函數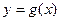 ,
,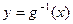 交于
交于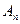 、
、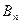 兩點,(其中
兩點,(其中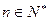 );設
);設 ,
,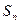 為數列
為數列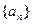 的前
的前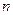 項和,求證:當
項和,求證:當 時,
時,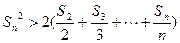 .
.
(本小題滿分14分)在平面直角坐標系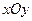 中,已知直線
中,已知直線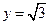 被圓
被圓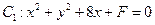 截得的弦長為
截得的弦長為 .
.
(Ⅰ)求圓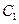 的方程;
的方程;
(Ⅱ)設圓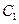 和
和 軸相交于A,B兩點,點P為圓
軸相交于A,B兩點,點P為圓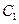 上不同于A,B的任意一點,直線
上不同于A,B的任意一點,直線 ,
,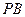 交
交 軸于M,N兩點.當點P變化時,以
軸于M,N兩點.當點P變化時,以 為直徑的圓
為直徑的圓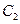 是否經過圓
是否經過圓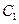 內一定點?請證明你的結論.
內一定點?請證明你的結論.
(本小題滿分14分)
已知曲線 上任意一點
上任意一點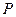 到兩個定點
到兩個定點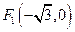 和
和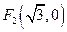 的距離之和為4.
的距離之和為4.
(1)求曲線 的方程;
的方程;
(2)設過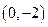 的直線
的直線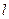 與曲線
與曲線 交于
交于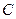 、
、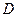 兩點,且
兩點,且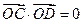 (
(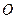 為坐標原點),求直線
為坐標原點),求直線 的方程.
的方程.
(執信中學、中山紀念中學、深圳外語)三校聯考 09.02
一.選擇題:
二.填空題:9.1;
10.15;
11.


13. ;
14.
;
14. ;
15.
;
15. .
.
三.解答題:
16.(1) =
= =
= 2分
2分
= =
= 4分
4分

 6分
6分
(2) =
= =
=
= =
= 9分
9分
由 ,得
,得 10分
10分

 11分
11分
 當
當 , 即
, 即 時,
時, 12分
12分
17.(1)由已知, 的取值為
的取值為 .
2分
.
2分
 ,
,  ,
,
 ,
,  8分
8分

7
8
9
10





 的分布列為:
的分布列為:
9分
(2) 11分
11分
 12分
12分
18.(1)由 .且
.且 得
得 2分
2分
 ,
,
 4分
4分
在 中,令
中,令 得
得 當
當 時,T
時,T =
=
 ,
,
兩式相減得 ,
, 6分
6分
 .
8分
.
8分
(2) ,
9分
,
9分
 ,
, , 10分
, 10分
 =2
=2
= ,
13分
,
13分
 14分
14分
19、(Ⅰ)在梯形 中,
中, ,
,


 四邊形
四邊形 是等腰梯形,
是等腰梯形,
且

 2分
2分
又 平面
平面 平面
平面 ,交線為
,交線為 ,
,
 平面
平面 4分
4分
(Ⅱ)解法一、當 時,
時, 平面
平面 ,
5分
,
5分
在梯形 中,設
中,設 ,連接
,連接 ,則
,則 6分
6分
 ,而
,而
 ,
7分
,
7分
 ,
, 四邊形
四邊形 是平行四邊形,
是平行四邊形, 8分
8分
又 平面
平面 ,
, 平面
平面
 平面
平面 9分
9分
解法二:當 時,
時, 平面
平面 ,
,
由(Ⅰ)知,以點 為原點,
為原點, 所在直線為坐標軸,建立空間直角坐標系, 5分
所在直線為坐標軸,建立空間直角坐標系, 5分
 則
則 ,
, ,
, ,
, ,
,
 ,
,
 平面
平面 ,
,

 平面
平面

 與
與 、
、 共面,
共面,