
題目列表(包括答案和解析)
在△![]() 中,已知
中,已知![]() ·
·![]() =9,sin
=9,sin![]() =cos
=cos![]() sin
sin![]() ,面積S
,面積S![]() =6.
=6.
(Ⅰ)求△![]() 的三邊的長;
的三邊的長;
(Ⅱ)設![]() 是△
是△![]() (含邊界)內一點,
(含邊界)內一點,![]() 到三邊
到三邊![]() ,
,![]() ,
,![]() 的距離分別為x,y和z,求x+y+z的取值范圍.
的距離分別為x,y和z,求x+y+z的取值范圍.
在 中,
中, 是三角形的三內角,
是三角形的三內角, 是三內角對應的三邊,已知
是三內角對應的三邊,已知 成等差數列,
成等差數列, 成等比數列
成等比數列
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 的值.
的值.
【解析】第一問中利用依題意 且
且 ,故
,故
第二問中,由題意 又由余弦定理知
又由余弦定理知

,得到 ,所以
,所以 ,從而得到結論。
,從而得到結論。
(1)依題意 且
且 ,故
,故 ……………………6分
……………………6分
(2)由題意 又由余弦定理知
又由余弦定理知
 …………………………9分
…………………………9分
即 故
故

 代入
代入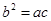 得
得

在 中,
中,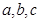 ,分別是角
,分別是角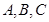 所對邊的長,
所對邊的長,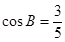 ,且
,且
(1)求 的面積;
的面積;
(2)若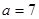 ,求角C.
,求角C.
【解析】第一問中,由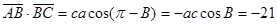 又∵
又∵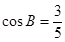 ∴
∴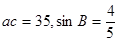 ∴
∴ 的面積為
的面積為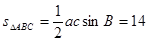
第二問中,∵a =7 ∴c=5由余弦定理得: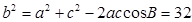 得到b的值,然后又由余弦定理得:
得到b的值,然后又由余弦定理得: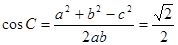
又C為內角 ∴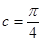
解:(1)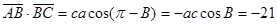 ………………2分
………………2分
又∵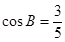 ∴
∴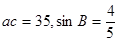 ……………………4分
……………………4分
∴ 的面積為
的面積為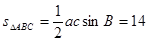 ……………………6分
……………………6分
(2)∵a =7 ∴c=5 ……………………7分
由余弦定理得: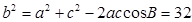
∴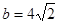 ……………………9分
……………………9分
又由余弦定理得: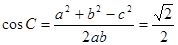
又C為內角 ∴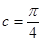 ……………………12分
……………………12分
另解:由正弦定理得: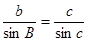 ∴
∴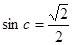 又
又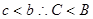 ∴
∴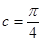
在![]() 中,∠A:∠B=1:2,∠
中,∠A:∠B=1:2,∠![]() 的平分線
的平分線![]() 分⊿ACD與⊿BCD的面積比是3:2,
分⊿ACD與⊿BCD的面積比是3:2,
則![]()
選擇題答題卡(請務必把答案填寫在答題卡內)
| 題號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
(9分)如圖,在四棱錐P—ABCD中,底面ABCD為矩形,側棱PA⊥底面ABCD,AB=,BC=1,PA=2,E為PD的中點.
(1)求直線BE與平面ABCD所成角的正切值;
(2)在側面PAB內找一點N,使NE⊥面PAC,
并求出N點到AB和AP的距離.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com