精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

設(shè)橢圓的左、右頂點(diǎn)分別為，點(diǎn)在橢圓上且異于兩點(diǎn)，為坐標(biāo)原點(diǎn).

（Ⅰ）若直線(xiàn)與的斜率之積為，求橢圓的離心率；

（Ⅱ）若，證明直線(xiàn)的斜率 滿(mǎn)足

【解析】(1)解：設(shè)點(diǎn)P的坐標(biāo)為.由題意，有  ①

由，得，

由，可得，代入①并整理得

由于，故.于是，所以橢圓的離心率

（2）證明：（方法一）

依題意，直線(xiàn)OP的方程為，設(shè)點(diǎn)P的坐標(biāo)為.

由條件得消去并整理得  ②

由，及，

得.

整理得.而，于是，代入②，

整理得

由，故，因此.

所以.

(方法二)

依題意，直線(xiàn)OP的方程為，設(shè)點(diǎn)P的坐標(biāo)為.

由P在橢圓上，有

因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012071821180638818491/SYS201207182118494193384555_ST.files/image036.png">，，所以，即   ③

由，，得整理得.

于是，代入③，

整理得

解得，

所以.

 

如圖,在正三棱柱ABC-A₁B₁C₁中,E∈BB_1，截面A₁EC⊥側(cè)面AC₁.

(Ⅰ)求證:BE=EB₁;

(Ⅱ)若AA₁=A₁B₁;求平面A₁EC與平面A₁B₁C₁所成二面角(銳角)的度數(shù).

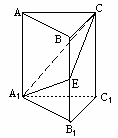
注意:在下面橫線(xiàn)上填寫(xiě)適當(dāng)內(nèi)容,使之成為(Ⅰ)的完整證明,并解答(Ⅱ).

(Ⅰ)證明:在截面A₁EC內(nèi),過(guò)E作EG⊥A₁C,G是垂足.

① ∵                                     

 ∴EG⊥側(cè)面AC₁;取AC的中點(diǎn)F,連結(jié)BF,FG,由AB=BC得BF⊥AC,

② ∵                             

 ∴BF⊥側(cè)面AC₁;得BF∥EG,BF、EG確定一個(gè)平面,交側(cè)面AC₁于FG.

③ ∵                      

 ∴BE∥FG,四邊形BEGF是平行四邊形,BE=FG,

④ ∵                            

 ∴FG∥AA₁,△AA₁C∽△FGC,

⑤ ∵                    

即，故

【答案】

【解析】設(shè)，有幾何意義知的最小值為， 又因?yàn)榇嬖趯?shí)數(shù)x滿(mǎn)足，所以只要2大于等于f（x）的最小值即可．即2，解得：∈，所以a的取值范圍是．故答案為：．

已知函數(shù)=.

(Ⅰ)當(dāng)時(shí)，求不等式 ≥3的解集；

(Ⅱ) 若≤的解集包含，求的取值范圍.

【命題意圖】本題主要考查含絕對(duì)值不等式的解法，是簡(jiǎn)單題.

【解析】(Ⅰ)當(dāng)時(shí)，=，

當(dāng)≤2時(shí)，由≥3得，解得≤1；

當(dāng)2＜＜3時(shí)，≥3，無(wú)解；

當(dāng)≥3時(shí)，由≥3得≥3，解得≥8，

∴≥3的解集為{|≤1或≥8}；

(Ⅱ) ≤，

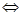
當(dāng)∈[1,2]時(shí)，==2，

∴，有條件得且，即，

故滿(mǎn)足條件的的取值范圍為[－3,0]

 

已知數(shù)列滿(mǎn)足（I）求數(shù)列的通項(xiàng)公式；

（II）若數(shù)列中，前項(xiàng)和為，且證明：

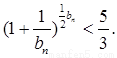
【解析】第一問(wèn)中，利用，

∴數(shù)列{}是以首項(xiàng)a₁+1，公比為2的等比數(shù)列，即 

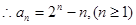
第二問(wèn)中， 

進(jìn)一步得到得    即

即是等差數(shù)列.

然后結(jié)合公式求解。

解：（I）  解法二、，

∴數(shù)列{}是以首項(xiàng)a₁+1，公比為2的等比數(shù)列，即 

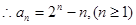
（II）     ………②

由②可得： …………③

③－②，得    即 …………④

又由④可得 …………⑤

⑤－④得

即是等差數(shù)列.