題目列表(包括答案和解析)
一段長為32米的籬笆圍成一個一邊靠墻的矩形菜園，墻長18米，問這個矩形的長、寬各為多少時，菜園的面積最大，最大面積是多少？
【解析】解：令矩形與墻垂直的兩邊為寬并設矩形寬為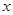
，則長為
所以矩形的面積
（
） （4分
=128 （8分）
當且僅當
時，即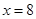
時等號成立，此時
有最大值128
所以當矩形的長為=16，寬為8時，
菜園面積最大，最大面積為128 （13分）答：當矩形的長為16米，寬為8米時。菜園面積最大，最大面積為128平方米（注：也可用二次函數模型解答）
| x+y |
| 2 |
| x+y |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| x+y |
| 2 |
| x+y |
| 2 |
| 1 |
| 2 |
| 2ab |
| a+b |
| a+b |
| 2 |
|
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| a |
| x |
| b |
| y |
| 1 |
| 3-tan2x |
| 9 |
| 8+sec2x |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com