題目列表(包括答案和解析)
已知函數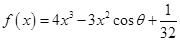
，其中
，
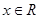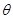為參數，且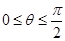
．
(1)當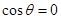
時，判斷函數
是否有極值；
(2)要使函數的極小值大于零，求參數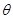的取值范圍；
(3)若對(2)中所求的取值范圍內的任意參數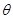，函數在區間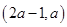
內都是增函數，求實數
的取值范圍．
已知函數
其中
為參數，且
（I）當
時，判斷函數
是否有極值；
（II）要使函數的極小值大于零，求參數
的取值范圍；
（III）若對（II）中所求的取值范圍內的任意參數，函數在區間
內都是增函數，求實數
的取值范圍。
已知函數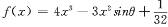
，其中
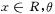為參數，且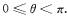
(I)當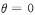
時，判斷函數
是否有極值，說明理由；
(II)要使函數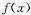
的極小值大于零，求參數
的取值范圍；
(III)若對（II)中所求的取值范圍內的任意參數，函數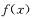
在區間(2a-1,a)內都是增函數，求實數a的取值范圍.
已知函數
，其中
,
為參數,且0≤≤
．
（1）當
時，判斷函數
是否有極值；
（2）要使函數的極小值大于零，求參數的取值范圍；
（3）若對（2）中所求的取值范圍內的任意參數，函數在區間
內都是增函數，求實數
的取值范圍。
已知函數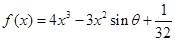
，其中
為參數，且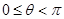
.
（1）當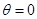
時，判斷函數
是否有極值，說明理由；
（2）要使函數的極小值大于零，求參數
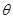的取值范圍；
（3）若對（2）中所求的取值范圍內的任意參數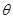，函數在區間
內都是增函數，求實數
的取值范圍。
一、選擇題：
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
A
B
D
B
C
B
C
D
B
1．提示：
，故選C。
2．提示：“任意的”否定為“存在”；“>”的否定為“
”,故選A
3．提示：
又
，所以
，故選D。
4．提示：在AB上取點D，使得
，則點P只能在AD內運動，則
，
5．提示：排除法選B。
6．提示：由圖（1）改為圖（2）后每次循環時
的值都為1，因此運行過程出現無限循環，故選D
7．提示：由莖葉圖的定義，甲得分為7，8，9，15，19，23，24，26，32，41。共11個數，19是中位數，乙得分為5，7，11，11，13，20，22，30，31，40。共11個數，13是中位數。
故選B。
8．提示：
得
所以
，故選C。
9．提示：由
及
得
如圖
過A作
于M,則
得
.
故選B.
10．提示：不妨設點（2，0）與曲線
上不同的三的點距離為分別
，它們組成的等比數列的公比為
若令
，顯然
，又
所以
，
不能取到
。故選B。
11．提示：使用特值法：取集合
當
可以排除A、B；
取集合
，當
可以排除C；故選D；
12．提示：n棱柱有
個頂點，被平面截去一個三棱錐后，可以分以下6種情形（圖1~6）
2在圖4，圖6所示的情形，還剩個頂點；
在圖5的情形，還剩
個頂點；
在圖2，圖3的情形，還剩
個頂點；
在圖1的情形，還剩下
個頂點.故選B.
二、填空題：
13．4
提示：
由（1），（2）得
或
，所以
。
14．
提示：斜率
，切點
，所以切線方程為：
15．
提示：當
時，不等式無解，當
時，不等式變為
，
由題意得
或
，所以，
或
16．
三、解答題：
17．解：① ∵
∴
的定義域為R；
② ∵
，
∴
為偶函數；
③ ∵
, ∴是周期為
的周期函數；
④ 當
時，=
，
∴當時單調遞減；當
時，
=
，
單調遞增；又∵是周期為的偶函數，∴在
上單調遞增，在
上單調遞減（
）；
⑤ ∵當
時
；
當
時
．∴的值域為
；
⑥由以上性質可得：在
上的圖象如圖所示：
18．解：（Ⅰ）取PC的中點G，連結EG，GD，則
由（Ⅰ）知FD⊥平面PDC，
面PDC，所以FD⊥DG。
所以四邊形FEGD為矩形，因為G為等腰Rt△RPD斜邊PC的中點，
所以DG⊥PC，
，則函數
上是增函數，故無極值；
得
。由
及（1）只考慮
的情況：
，且
，所以
；
內都是增函數，又函數
內是增函數，則
，由（2）
時
要使得不等式
關于參數
恒成立，必有
，
所以
的取值范圍是
900=234人
，
時，
，
適合上式，
時，
，則數列
是等差數列，首項為1，公差為1。
恒成立，
恒成立，
恒成立。
為奇數時，即
恒成立，又
的最小值為1，
恒成立，又
的最大值為
，
又
為整數，
，使得對任意
，都有
則
而
，故
，
在區間
上單調遞增。
得
函數
時，
取得最小值，此時點F、G的坐標分別為
，由于點G在橢圓上，得
。
，則
，得
，
，
，
得
。又
，解得
