
題目列表(包括答案和解析)
 的最小值,指出下列解法的錯(cuò)誤,并給出正確解法.
的最小值,指出下列解法的錯(cuò)誤,并給出正確解法. .∴
.∴ .
. 當(dāng)
當(dāng) 即
即 時(shí),
時(shí), .
.已知函數(shù) 的最小值為0,其中
的最小值為0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若對(duì)任意的 有
有 ≤
≤ 成立,求實(shí)數(shù)
成立,求實(shí)數(shù) 的最小值;
的最小值;
(Ⅲ)證明 (
( ).
).
【解析】(1)解:
 的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012071821180638818491/SYS201207182118530600520067_ST.files/image010.png">
的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012071821180638818491/SYS201207182118530600520067_ST.files/image010.png">

由 ,得
,得
當(dāng)x變化時(shí), ,
, 的變化情況如下表:
的變化情況如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
極小值 |
|
因此, 在
在 處取得最小值,故由題意
處取得最小值,故由題意 ,所以
,所以
(2)解:當(dāng) 時(shí),取
時(shí),取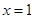 ,有
,有 ,故
,故 時(shí)不合題意.當(dāng)
時(shí)不合題意.當(dāng)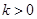 時(shí),令
時(shí),令 ,即
,即

令 ,得
,得
①當(dāng) 時(shí),
時(shí), ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上單調(diào)遞減.從而對(duì)于任意的
上單調(diào)遞減.從而對(duì)于任意的 ,總有
,總有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合題意.
符合題意.
②當(dāng) 時(shí),
時(shí), ,對(duì)于
,對(duì)于 ,
, ,故
,故 在
在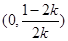 上單調(diào)遞增.因此當(dāng)取
上單調(diào)遞增.因此當(dāng)取 時(shí),
時(shí), ,即
,即 不成立.
不成立.
故 不合題意.
不合題意.
綜上,k的最小值為 .
.
(3)證明:當(dāng)n=1時(shí),不等式左邊= =右邊,所以不等式成立.
=右邊,所以不等式成立.
當(dāng) 時(shí),
時(shí),


在(2)中取 ,得
,得
 ,
,
從而

所以有





綜上,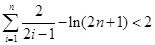 ,
,
| 3 |
| x |
| 3 |
| x |
| 1 |
| x |
| 1 |
| x |
| 3 | 2x2•
| ||||
| 3 | 4 |
| 3 | 4 |
| 3 |
| x |
2x2•
|
| 6x |
| 3 |
| x |
| |||
| 2 |
6•
|
3
|
| 6 | 324 |
已知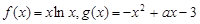
(1)求函數(shù)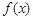 在
在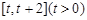 上的最小值
上的最小值
(2)對(duì)一切的 恒成立,求實(shí)數(shù)a的取值范圍
恒成立,求實(shí)數(shù)a的取值范圍
(3)證明對(duì)一切 ,都有
,都有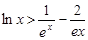 成立
成立
【解析】第一問中利用
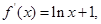 當(dāng)
當(dāng)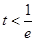 時(shí),
時(shí),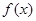 在
在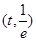 單調(diào)遞減,在
單調(diào)遞減,在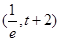 單調(diào)遞增
單調(diào)遞增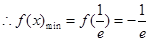 ,當(dāng)
,當(dāng)
 ,即
,即 時(shí),
時(shí),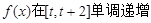 ,
,
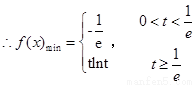
第二問中,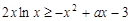 ,則
,則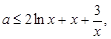 設(shè)
設(shè) ,
,
則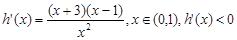 ,
, 單調(diào)遞增,
單調(diào)遞增, ,
, ,
, 單調(diào)遞減,
單調(diào)遞減,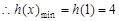 ,因?yàn)閷?duì)一切
,因?yàn)閷?duì)一切 ,
,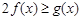 恒成立,
恒成立,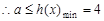
第三問中問題等價(jià)于證明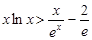 ,
, ,
,
由(1)可知 ,
, 的最小值為
的最小值為 ,當(dāng)且僅當(dāng)x=
,當(dāng)且僅當(dāng)x= 時(shí)取得
時(shí)取得
設(shè) ,
, ,則
,則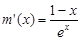 ,易得
,易得
 。當(dāng)且僅當(dāng)x=1時(shí)取得.從而對(duì)一切
。當(dāng)且僅當(dāng)x=1時(shí)取得.從而對(duì)一切 ,都有
,都有 成立
成立
解:(1)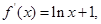 當(dāng)
當(dāng)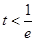 時(shí),
時(shí),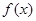 在
在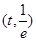 單調(diào)遞減,在
單調(diào)遞減,在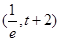 單調(diào)遞增
單調(diào)遞增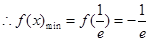 ,當(dāng)
,當(dāng)
 ,即
,即 時(shí),
時(shí),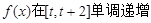 ,
,
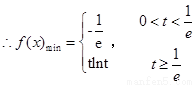 …………4分
…………4分
(2)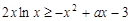 ,則
,則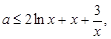 設(shè)
設(shè) ,
,
則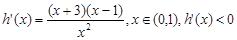 ,
, 單調(diào)遞增,
單調(diào)遞增, ,
, ,
, 單調(diào)遞減,
單調(diào)遞減,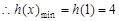 ,因?yàn)閷?duì)一切
,因?yàn)閷?duì)一切 ,
,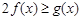 恒成立,
恒成立,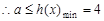 …………9分
…………9分
(3)問題等價(jià)于證明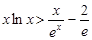 ,
, ,
,
由(1)可知 ,
, 的最小值為
的最小值為 ,當(dāng)且僅當(dāng)x=
,當(dāng)且僅當(dāng)x= 時(shí)取得
時(shí)取得
設(shè) ,
, ,則
,則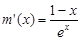 ,易得
,易得
 。當(dāng)且僅當(dāng)x=1時(shí)取得.從而對(duì)一切
。當(dāng)且僅當(dāng)x=1時(shí)取得.從而對(duì)一切 ,都有
,都有 成立
成立
| 3 |
| x |
| 3 |
| x |
| 1 |
| x |
| 1 |
| x |
| 3 | 2x2•
| ||||
| 3 | 4 |
| 3 | 4 |
| 3 |
| x |
2x2•
|
| 6x |
| 3 |
| x |
| |||
| 2 |
6•
|
3
|
| 6 | 324 |
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com