
題目列表(包括答案和解析)
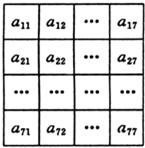 13、把49個數排成如圖所示的數表,若表中每行的7個數自左至右依次都成等差數列,每列的7個數自上而下依次也都成等差數列,且正中間的數a44=1,則表中所有數的和為
13、把49個數排成如圖所示的數表,若表中每行的7個數自左至右依次都成等差數列,每列的7個數自上而下依次也都成等差數列,且正中間的數a44=1,則表中所有數的和為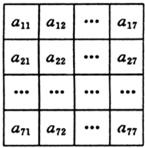
 把49個數排成如圖所示的數表,若表中每行的7個數自左至右依次都成等差數列,每列的7個數自上而下依次也都成等差數列,且正中間的數a44=1,則表中所有數的和為________.
把49個數排成如圖所示的數表,若表中每行的7個數自左至右依次都成等差數列,每列的7個數自上而下依次也都成等差數列,且正中間的數a44=1,則表中所有數的和為________.把49個數排成如圖所示的數表,若表中每行的7個數自左至右依次都成等差數列,每列的7個數自上而下依次也都成等差數列,且正中間的數a![]() =1,則表中所有數的和為 _____________。
=1,則表中所有數的和為 _____________。
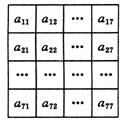
把49個數排成如圖所示的數表,若表中每行的7個數自左至右依次都成等差數列,每列的7個數自上而下依次也都成等差數列,且正中間的數a44=1,則表中所有數的和為________.
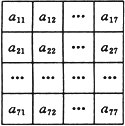
一、 選擇題:
1、答案:D
解:②表示垂直于同一平面的兩條直線互相平行;
③表示垂直于同一直線的兩個平面互相平行;
2、答案:D ;
解: ,非P真;又
,非P真;又 真,所以選D;
真,所以選D;
3、答案:B ;
解: 本題考查了正方體堆壘問題及數列通項公式的求解.列出該數列的前幾項,通過相鄰項間的關系可得出該數列的規律而得出一等差數列.
本題考查了正方體堆壘問題及數列通項公式的求解.列出該數列的前幾項,通過相鄰項間的關系可得出該數列的規律而得出一等差數列.
由圖示可得,該正方體的個數所組成的數列1,3,6,…, 其后一項減前一項得一數列2,3,4,…為一個等差數列.由此可得第6層的正方體的個數為1,3,6,10,15,21,… ,
故應選B.
4、答案:D ;
解: 的圖象向右平移
的圖象向右平移 單位后得到:
單位后得到: ,故選D;
,故選D;
5、答案:B ;
解:據題意可知集合A表示函數 的定義域,
的定義域, ,易化簡得
,易化簡得 ,由于B
,由于B A,故當
A,故當 時,即
時,即 時易知符合題意;當
時易知符合題意;當 時,
時, ,要使B
,要使B A,結合數軸知需
A,結合數軸知需 或
或 (經驗證符合題意)或
(經驗證符合題意)或 (經驗證不合題意舍去),解得
(經驗證不合題意舍去),解得 ,故綜上所述可知滿足條件的
,故綜上所述可知滿足條件的 的取值范圍是
的取值范圍是 ,故答案為B;
,故答案為B;
6、答案:D ;
解:由圖象變換可以得到兩個圖象間的關系,函數 是由函數
是由函數 的圖象向右平移一個單位得到,而
的圖象向右平移一個單位得到,而 是由函數
是由函數 的圖象關于y軸對稱得到
的圖象關于y軸對稱得到 再向右平移一個單位得到,故兩函數的圖象關于直線
再向右平移一個單位得到,故兩函數的圖象關于直線 對稱。故選D
對稱。故選D
7、答案:B ;
解:兩直線平行,則其斜率相等,利用兩點間直線的斜率公式可以得兩字母 間的關系,于是可得兩點間的距離.
間的關系,于是可得兩點間的距離.
由題意得
所以 故應選B.
故應選B.
8、答案:B ;
解:由于 ,故函數的定義域為
,故函數的定義域為 ,根據已知0<a<b<c,則易將函數解析式化簡為
,根據已知0<a<b<c,則易將函數解析式化簡為 =
=  ,故
,故 且其定義域關于原點對稱,即函數為偶函數,其圖象關于y軸對稱。故應選B.
且其定義域關于原點對稱,即函數為偶函數,其圖象關于y軸對稱。故應選B.
9、答案:C ;
解:本題考查直線的斜率,由垂直關系得兩直線的斜率之積為 ,再由均值不等式轉化轉化得出不等關系式,分類討論得出
,再由均值不等式轉化轉化得出不等關系式,分類討論得出 的最小值.由題意
的最小值.由題意 ,
,
∵兩直線互相垂直,
∴ ,即
,即 ,
,
∴ ,則
,則 .
.
當 時,
時, ;當
;當 時,
時, .
.
綜合得 的最小值為
的最小值為 . 故應選C.
. 故應選C.
10、答案:C ;
解:由題意可知,存在 ,使
,使 ,即
,即 ,從函數定義出發,畫出映射幫助思考,從A到B再到C是由題意可得,如果繼續對C集合中的
,從函數定義出發,畫出映射幫助思考,從A到B再到C是由題意可得,如果繼續對C集合中的 ,應用法則
,應用法則 ,則會得到
,則會得到 ,從B到C再到D的映射為
,從B到C再到D的映射為 ,即存在
,即存在 ,使
,使 ,即函數
,即函數 過點
過點 ,即方程
,即方程 有解,易知
有解,易知 在實數集R上無解故選D。
在實數集R上無解故選D。
二、 填空題:
11、答案:1 ;
解:根據集合中元素的確定性,我們不難得到兩集合的元素是相同的,這樣需要列方程組分類討論,顯然復雜又煩瑣.這時若能發現0這個特殊元素,和 中的a不為0的隱含信息,就能得到如下解法.由已知得
中的a不為0的隱含信息,就能得到如下解法.由已知得 =0,及a≠0,所以b=0,于是a2=1,即a=1或a=-1,又根據集合中元素的互異性a=1應舍去,因而a=-1,故a2008+b2008=(-1) 2008=1.
=0,及a≠0,所以b=0,于是a2=1,即a=1或a=-1,又根據集合中元素的互異性a=1應舍去,因而a=-1,故a2008+b2008=(-1) 2008=1.
12、答案:120度;
解:依題意可知: A、O、B、C構成平形四邊形,
A、O、B、C構成平形四邊形, ,故
,故 的內角C為120度;
的內角C為120度;
13、答案: ;
;
解: 

 .
.
14、答案: ;
;
解: ,設
,設 ,依題意可知:
,依題意可知: ,又P在曲線上,故
,又P在曲線上,故 ,故點P的坐標為
,故點P的坐標為 ;
;
15、答案:49 ;
解:本題考查用取特殊值法進行驗證.由題意分析,
不妨設各個格中的數都為1, 則符合題意要求,所以表中所有數字之和為49.
三、 解答題:
16、 解:(1)因為
 ,
,
所以 .
.
(2)由 即
即 ,
,
亦即 .
.
故 ,
,
當且僅當 時取得等號.
時取得等號.
又 .
.
故當 時有
時有 有最大值
有最大值 .
.
17、 解:(Ⅰ)從九個小球中任取三個共有 種取法,它們是等可能的.設恰好有一球編號是3的倍數的事件為A,
種取法,它們是等可能的.設恰好有一球編號是3的倍數的事件為A,
則 .
.
(Ⅱ)設至少有一球編號是3的倍數的事件為B,
則 .
.
(Ⅲ)設三個小球編號之和是3的倍數的事件為C,設集合 ,
,  ,則取出三個小球編號之和為3的倍數的取法共有
,則取出三個小球編號之和為3的倍數的取法共有 種,則
種,則 .
.
18、解:設橢圓方程為
(Ⅰ)易得所求橢圓方程為 .
.
(Ⅱ)解法一:由題意知直線 的斜率存在,設直線
的斜率存在,設直線 的方程為
的方程為
由 ,消去y得關于x的方程:
,消去y得關于x的方程:
由直線 與橢圓相交于A、B兩點,
與橢圓相交于A、B兩點, 解得
解得
又由韋達定理得

 原點
原點 到直線
到直線 的距離
的距離
 .
.
對 兩邊平方整理得:
兩邊平方整理得: (*)∵
(*)∵ ,
,
 整理得:
整理得: 又
又 ,
, 從而
從而 的最大值為
的最大值為 ,此時代入方程(*)得
,此時代入方程(*)得 

所以,所求直線方程為: .
.
19、(Ⅰ)解:(1)3-k2>1-k>0 k∈(-1,1),方程所表示的曲線是焦點在x軸上的橢圓;
k∈(-1,1),方程所表示的曲線是焦點在x軸上的橢圓;
(2) 1-k>3-k2>0 k∈(-
k∈(- ,-1),方程所表示的曲線是焦點在y軸上的橢圓;
,-1),方程所表示的曲線是焦點在y軸上的橢圓;
(3)1-k=3-k2>0 k=-1,表示的是一個圓;
k=-1,表示的是一個圓;
(4)(1-k)(3-k2)<0 k∈(-∞,-
k∈(-∞,- )∪(1,
)∪(1, ),表示的是雙曲線;
),表示的是雙曲線;
(5)k=1,k=- ,表示的是兩條平行直線;k=
,表示的是兩條平行直線;k= ,表示的圖形不存在.
,表示的圖形不存在.
(Ⅱ)解:依題意,設雙曲線的方程為 -
- =1(a>0,b>0).∵e=
=1(a>0,b>0).∵e= =
= ,c2=a2+b2,∴a2=4b2.
,c2=a2+b2,∴a2=4b2.
設M(x,y)為雙曲線上任一點,則|PM|2=x2+(y-5)2=b2( -1)+(y-5)2=
-1)+(y-5)2= (y-4)2+5-b2(|y|≥2b).
(y-4)2+5-b2(|y|≥2b).
①若4≥2b,則當y=4時,|PM|min2=5-b2=4,得b2=1,a2=4.從而所求雙曲線方程為 -x2=1.
-x2=1.
②若4<2b,則當y=2b時,|PM|min2=4b2-20b+25=4,得b= (舍去b=
(舍去b= ),b2=
),b2= ,a2=49.
,a2=49.
從而所求雙曲線方程為 -
- =1.
=1.
20、解:如圖,連結 ,由
,由 為
為 中點,則
中點,則 從而
從而 .故AM和
.故AM和 所成的角為
所成的角為 所成的角,易證
所成的角,易證 ≌
≌ 。所以
。所以 ,故
,故 所成的角為
所成的角為 。又設AB的中點為Q,則
。又設AB的中點為Q,則 又
又 從而CN與AM所成的角就是
從而CN與AM所成的角就是 (或其補角)。易求得
(或其補角)。易求得 在
在 中,由余弦定理得
中,由余弦定理得 ,故
,故 所成的角為
所成的角為 。
。
21、解 (1)當a=1,b=?2時,f(x)=x2?x?3,
(1)當a=1,b=?2時,f(x)=x2?x?3,
(2)∵f(x)=ax2+(b+1)x+(b?1)(a≠0)恒有兩個不動點,
∴x=ax2+(b+1)x+(b?1),
即ax2+bx+(b?1)=0恒有兩相異實根
于是Δ′=(
(3)由題意A、B兩點應在直線y=x上,設A(x1,x1),B(x2,x2)
∴x′=y′= ,
,
又點M在直線 上有
上有 ,
,
即
∵a>0,∴ ≥2
≥2 當且僅當
當且僅當 即a=
即a= ∈(0,1)時取等號,
∈(0,1)時取等號,
作者: 湖南省衡陽市祁東縣育賢中學 高明生 彭鐵軍
PC: 421600
TEL: 0734---6184532
Cellphone: 13187168216
E―mail: hunanqidonggms@163.com
QQ: 296315069
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com