
題目列表(包括答案和解析)
已知圓![]() ,圓上各點的縱坐標保持不變,橫坐標伸長到原來的
,圓上各點的縱坐標保持不變,橫坐標伸長到原來的![]() 倍,得一橢圓E,
倍,得一橢圓E,
(1)求橢圓E的方程,并證明橢圓E的離心率是與![]() 無關的常數;
無關的常數;
(2)若m=1,是否存在直線![]() 過P(0,2),與橢圓交于M、N兩點,且滿足
過P(0,2),與橢圓交于M、N兩點,且滿足![]() =0(O為坐標原點)?若存在,求出直線
=0(O為坐標原點)?若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
| an | 2n |
已知數列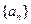 滿足:
滿足: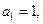
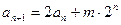
 (
(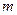 是與無關的常數且
是與無關的常數且 ).
).
(Ⅰ) 設 ,證明數列
,證明數列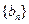 是等差數列,并求
是等差數列,并求 ;
;
(Ⅱ) 若數列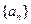 是單調遞減數列,求
是單調遞減數列,求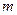 的取值范圍.
的取值范圍.
(本小題滿分12分)
設同時滿足條件:①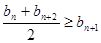 ;②
;②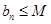 (
( ,
,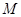 是與
是與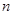 無關的常數)的無窮數列
無關的常數)的無窮數列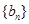 叫“嘉文”數列.已知數列
叫“嘉文”數列.已知數列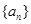 的前
的前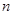 項和
項和 滿足:
滿足: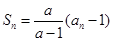 (
(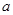 為常數,且
為常數,且 ,
,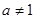 ).
).
(Ⅰ)求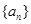 的通項公式;[來源:學*科*網Z*X*X*K]
的通項公式;[來源:學*科*網Z*X*X*K]
(Ⅱ)設 ,若數列
,若數列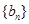 為等比數列,求
為等比數列,求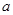 的值,并證明此時
的值,并證明此時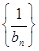 為“嘉文”數列.
為“嘉文”數列.
設集合W是滿足下列兩個條件的無窮數列{an}的集合:①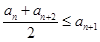 , ②
, ②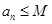 .其中
.其中 ,
, 是與
是與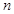 無關的常數.
無關的常數.
(Ⅰ)若{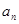 }是等差數列,
}是等差數列,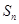 是其前
是其前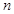 項的和,
項的和, ,
, ,證明:
,證明: ;
;
(Ⅱ)設數列{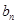 }的通項為
}的通項為 ,且
,且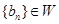 ,求
,求 的取值范圍;
的取值范圍;
(Ⅲ)設數列{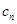 }的各項均為正整數,且
}的各項均為正整數,且 .證明
.證明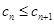 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com