
題目列表(包括答案和解析)
如圖,直三棱柱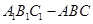 中,
中,
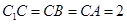 ,
,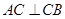 .
. 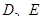 分別為棱
分別為棱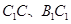 的中點.
的中點.
(1)求二面角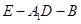 的平面角的余弦值;
的平面角的余弦值;
(2)在線段 上是否存在一點
上是否存在一點 ,使得
,使得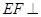 平
平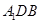 ?
?
若存在,確定其位置;若不存在,說明理由.
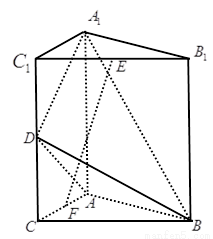
如圖,直三棱柱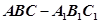 中,AB=BC,
中,AB=BC,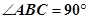 ,Q是AC上的點,AB1//平面BC1Q.
,Q是AC上的點,AB1//平面BC1Q.

(Ⅰ)確定點Q在AC上的位置;
(Ⅱ)若QC1與平面BB1C1C所成角的正弦值為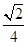 ,求二面角Q-BC1—C的余弦值.
,求二面角Q-BC1—C的余弦值.
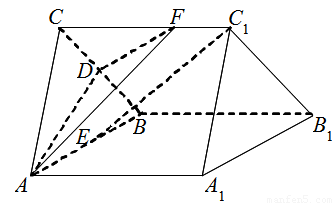
如圖,直三棱柱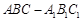 中,
中,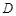 、
、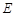 分別是棱
分別是棱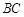 、
、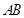 的中點,點
的中點,點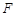 在棱
在棱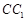 上,已知
上,已知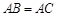 ,
, ,
,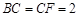 .
.
(1)求證: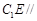 平面
平面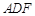 ;
;
(2)設點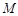 在棱
在棱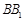 上,當
上,當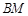 為何值時,平面
為何值時,平面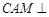 平面
平面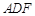 ?
?
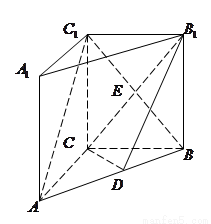
在如圖的直三棱柱
 中,
中,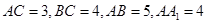 ,點
,點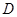 是
是 的中點.
的中點.
(1)求證: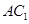 ∥平面
∥平面 ;
;
(2)求異面直線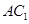 與
與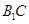 所成的角的余弦值;
所成的角的余弦值;
(3)求直線 與平面
與平面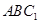 所成角的正弦值;
所成角的正弦值;
(本小題滿分12分)如圖,斜三棱柱![]() 中,
中,![]() 在底面的射影
在底面的射影![]() 恰好是
恰好是![]() 的中點,側棱與底面成
的中點,側棱與底面成![]() 角,側面
角,側面![]() 與側面
與側面![]() 成
成![]() 角.
角.
(1)求證:四邊形![]() 是矩形;(2)求斜三棱柱
是矩形;(2)求斜三棱柱![]() 的體積.
的體積.
數 學(理科) 2009.4
一、選擇題:本大題共有10小題,每小題5分,共50分.
題號
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
B
A
C
C
B
B
二、填空題:本大題共有7小題,每小題4分,共28分.
11.
-1 12. 110 13. 78 14. 15.
15. 16. 7 17.
16. 7 17.
三.解答題:本大題共5小題,共72分.解答應寫出文字說明、證明過程或演算步驟.
18.(Ⅰ)解: .……………………… 4分
.……………………… 4分
由 ,解得
,解得  .
.
所以函數 的單調遞增區間為
的單調遞增區間為  .…………… 7分
.…………… 7分
(Ⅱ)解:由 ,得
,得 .故
.故 .……………… 10分
.……………… 10分
于是有  ,或
,或 ,
,
即 或
或 .因
.因 ,故
,故 .……………… 14分
.……………… 14分
19.(Ⅰ)解:恰好摸到兩個“心”字球的取法共有4種情形:
開心心,心開心,心心開,心心樂.
則恰好摸到2個“心”字球的概率是
 .………………………………………6分
.………………………………………6分
(Ⅱ)解: ,
,
則  ,
, ,
,
 .…………………………………………10分
.…………………………………………10分
故取球次數 的分布列為
的分布列為

1
2
3




 .…………………………………………………14分
.…………………………………………………14分
20.(Ⅰ)解:因 在底面
在底面 上的射影恰為B點,則
上的射影恰為B點,則 ⊥底面
⊥底面 .
.
所以 就是
就是 與底面
與底面 所成的角.
所成的角.
因 ,故
,故  ,
,
即 與底面
與底面 所成的角是
所成的角是 .……………………………………………3分
.……………………………………………3分
 如圖,以A為原點建立空間直角坐標系,則
如圖,以A為原點建立空間直角坐標系,則
 ,
,
 ,
, .
.
則 ,
,
故 與棱BC所成的角是
與棱BC所成的角是 .…………………………………………………7分
.…………………………………………………7分
(Ⅱ)解:設 ,則
,則 .于是
.于是
 (
( 舍去),
舍去),
則P為棱 的中點,其坐標為
的中點,其坐標為 .…………………………………………9分
.…………………………………………9分
設平面 的法向量為
的法向量為 ,則
,則
 ,故
,故 .…………………11分
.…………………11分
而平面 的法向量是
的法向量是 ,
,
則 ,
,
故二面角 的平面角的余弦值是
的平面角的余弦值是 .………………………………14分
.………………………………14分
21.(Ⅰ)解:由題意知: ,
, ,
, ,解得
,解得 .
.
故橢圓的方程為 .…………………………………………………5分
.…………………………………………………5分
(Ⅱ)解:設 ,
,
⑴若 軸,可設
軸,可設 ,因
,因 ,則
,則 .
.
由 ,得
,得 ,即
,即 .
.
若 軸,可設
軸,可設 ,同理可得
,同理可得 .……………………7分
.……………………7分
⑵當直線 的斜率存在且不為0時,設
的斜率存在且不為0時,設 ,
,
由 ,消去
,消去 得:
得: .
.
則 .………………………………………9分
.………………………………………9分
 .
.
由 ,知
,知 .
.
故  ,即
,即 (記為①).…………11分
(記為①).…………11分
由 ,可知直線
,可知直線 的方程為
的方程為 .
.
聯立方程組 ,得
,得  (記為②).……………………13分
(記為②).……………………13分
將②代入①,化簡得 .
.
綜合⑴、⑵,可知點 的軌跡方程為
的軌跡方程為 .………………………15分
.………………………15分
22.(Ⅰ)證明:當 時,
時, .令
.令 ,則
,則 .
.
若 ,
, 遞增;若
遞增;若 ,
, 遞減,
遞減,
則 是
是 的極(最)大值點.于是
的極(最)大值點.于是
 ,即
,即 .故當
.故當 時,有
時,有 .………5分
.………5分
(Ⅱ)解:對 求導,得
求導,得 .
.
①若 ,
, ,則
,則 在
在 上單調遞減,故
上單調遞減,故 合題意.
合題意.
②若 ,
, .
.
則必須 ,故當
,故當 時,
時, 在
在 上單調遞增.
上單調遞增.
③若 ,
, 的對稱軸
的對稱軸 ,則必須
,則必須 ,
,
故當 時,
時, 在
在 上單調遞減.
上單調遞減.
綜合上述, 的取值范圍是
的取值范圍是 .………………………………10分
.………………………………10分
(Ⅲ)解:令 .則問題等價于
.則問題等價于
找一個 使
使 成立,故只需滿足函數的最小值
成立,故只需滿足函數的最小值 即可.
即可.
因 ,
,
而 ,
,
故當 時,
時, ,
, 遞減;當
遞減;當 時,
時, ,
, 遞增.
遞增.
于是, .
.
與上述要求 相矛盾,故不存在符合條件的
相矛盾,故不存在符合條件的 .……………………15分
.……………………15分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com