
題目列表(包括答案和解析)
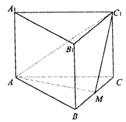
(08年濰坊市六模) (12分)如圖,正三棱柱![]() 的底面邊長為a,點M在邊BC上,△
的底面邊長為a,點M在邊BC上,△![]() 是以點M為直角頂點的等腰直角三角形.
是以點M為直角頂點的等腰直角三角形.
(1)求證點M為邊BC的中點;
(2)求點C到平面![]() 的距離;
的距離;
(3)求二面角![]() 的大小.
的大小.
把正方形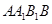 以邊
以邊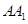 所在直線為軸旋轉
所在直線為軸旋轉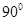 到正方形
到正方形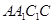 ,其中
,其中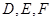 分別為
分別為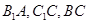 的中點.
的中點.
(1)求證: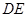 ∥平面
∥平面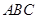 ;
;
(2)求證: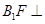 平面
平面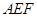 ;
;
(3)求二面角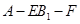 的大小.
的大小.
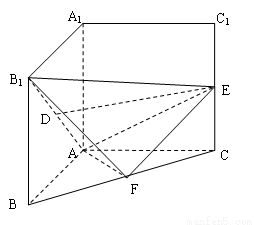
(本題滿分16分)如圖,在四棱錐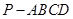 中,底面
中,底面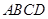 是
是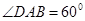 且邊長為
且邊長為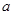 的菱形,側面
的菱形,側面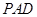 是等邊三角形,且平面
是等邊三角形,且平面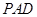 垂直于底面
垂直于底面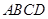 .
.
(1)若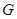 為
為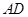 的中點,求證:
的中點,求證: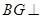 平面
平面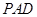 ;
;
(2)求證: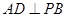 ;
;
(3)求二面角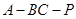 的大小.
的大小.
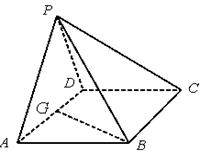
如圖,正方形![]() 所在的平面與平面
所在的平面與平面![]() 垂直,
垂直,![]() 是
是![]() 和
和![]() 的交點,
的交點,![]() ,且
,且![]() .
.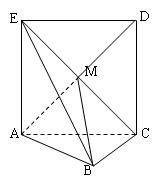
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成的角的大小;
所成的角的大小;
(3)求二面角![]() 的大小.
的大小.
在四棱錐 中,底面
中,底面 是正方形,側棱
是正方形,側棱 底面
底面 ,
, 的中點,作
的中點,作
(1)證明: ;
;
(2)證明: ;
;
(3)求二面角 的大小。
的大小。

一、CABCB BDADD AC
二、13. 0.1;14. ;15. 36;16.存在,通項公式
;15. 36;16.存在,通項公式 。
。
三、
17.解:(1)依題意得:

得: ,
,
所以: ,即
,即 ,………………………………4分
,………………………………4分