
題目列表(包括答案和解析)
已知函數 ,(
,(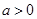 ),
),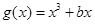
(1)若曲線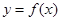 與曲線
與曲線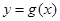 在它們的交點(1,c)處具有公共切線,求a,b的值
在它們的交點(1,c)處具有公共切線,求a,b的值
(2)當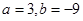 時,若函數
時,若函數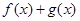 在區間[k,2]上的最大值為28,求k的取值范圍
在區間[k,2]上的最大值為28,求k的取值范圍
【解析】(1)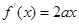 ,
,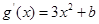
∵曲線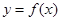 與曲線
與曲線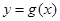 在它們的交點(1,c)處具有公共切線
在它們的交點(1,c)處具有公共切線
∴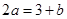 ,
,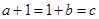
∴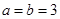
(2)當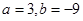 時,
時,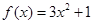 ,
,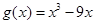 ,
,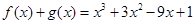
令 ,則
,則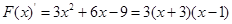 ,令
,令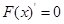 ,
, ∴
∴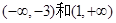 為單調遞增區間,
為單調遞增區間,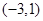 為單調遞減區間,其中F(-3)=28為極大值,所以如果區間[k,2]最大值為28,即區間包含極大值點
為單調遞減區間,其中F(-3)=28為極大值,所以如果區間[k,2]最大值為28,即區間包含極大值點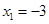 ,所以
,所以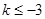
【考點定位】此題應該說是導數題目中較為常規的類型題目,考查的切線,單調性,極值以及最值問題都是課本中要求的重點內容,也是學生掌握比較好的知識點,在題目中能夠發現F(-3)=28,和分析出區間[k,2]包含極大值點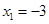 ,比較重要
,比較重要
根據定義討論(或證明)函數增減性的一般步驟是:
(1)設x1、x2是給定區間內的任意兩個值且x1<x2;
(2)作差f(x1)-f(x2),并將此差化簡、變形;
(3)判斷f(x1)-f(x2)的正負,從而證得函數的增減性.
利用函數的單調性可以把函數值的大小比較的問題轉化為自變量的大小比較的問題.
函數的單調性只能在函數的定義域內來討論.這即是說,函數的單調區間是其定義域的________.
(本小題滿分12分)某產品按質量分為10個檔次,生產第一檔(即最低檔次)的利潤是每件8元,每提高一個檔次,利潤每件增加2元,但每提高一個檔次,在相同的時間內,產量減少3件。如果在規定的時間內,最低檔次的產品可生產60件
(I)請寫出相同時間內產品的總利潤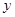 與檔次
與檔次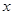 之間的函數關系式,并寫出
之間的函數關系式,并寫出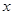 的定義域
的定義域
(II)在同樣的時間內,生產哪一檔次產品的總利潤最大?并求出最大利潤.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com