
題目列表(包括答案和解析)
如圖, ,
,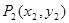 ,…,
,…, ,…是曲線
,…是曲線 上的點(diǎn),
上的點(diǎn), ,
, ,…,
,…, ,…是
,…是 軸正半軸上的點(diǎn),且
軸正半軸上的點(diǎn),且 ,
, ,…,
,…, ,…
均為斜邊在
,…
均為斜邊在 軸上的等腰直角三角形(
軸上的等腰直角三角形( 為坐標(biāo)原點(diǎn)).
為坐標(biāo)原點(diǎn)).
(1)寫出 、
、 和
和 之間的等量關(guān)系,以及
之間的等量關(guān)系,以及 、
、 和
和 之間的等量關(guān)系;
之間的等量關(guān)系;
(2)求證: (
( );
);
(3)設(shè) ,對(duì)所有
,對(duì)所有 ,
, 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù) 的取值范圍.
的取值范圍.

【解析】第一問利用有 ,
, 得到
得到
第二問證明:①當(dāng) 時(shí),可求得
時(shí),可求得 ,命題成立;②假設(shè)當(dāng)
,命題成立;②假設(shè)當(dāng) 時(shí),命題成立,即有
時(shí),命題成立,即有 則當(dāng)
則當(dāng) 時(shí),由歸納假設(shè)及
時(shí),由歸納假設(shè)及 ,
,
得
第三問

 .………………………2分
.………………………2分
因?yàn)楹瘮?shù) 在區(qū)間
在區(qū)間 上單調(diào)遞增,所以當(dāng)
上單調(diào)遞增,所以當(dāng) 時(shí),
時(shí), 最大為
最大為 ,即
,即

解:(1)依題意,有 ,
, ,………………4分
,………………4分
(2)證明:①當(dāng) 時(shí),可求得
時(shí),可求得 ,命題成立;
……………2分
,命題成立;
……………2分
②假設(shè)當(dāng) 時(shí),命題成立,即有
時(shí),命題成立,即有 ,……………………1分
,……………………1分
則當(dāng) 時(shí),由歸納假設(shè)及
時(shí),由歸納假設(shè)及 ,
,
得 .
.
即
解得 (
( 不合題意,舍去)
不合題意,舍去)
即當(dāng) 時(shí),命題成立. …………………………………………4分
時(shí),命題成立. …………………………………………4分
綜上所述,對(duì)所有 ,
, . ……………………………1分
. ……………………………1分
(3)

 .………………………2分
.………………………2分
因?yàn)楹瘮?shù) 在區(qū)間
在區(qū)間 上單調(diào)遞增,所以當(dāng)
上單調(diào)遞增,所以當(dāng) 時(shí),
時(shí), 最大為
最大為 ,即
,即
 .……………2分
.……………2分
由題意,有
 .
所以,
.
所以,
已知函數(shù)
 ;
;
(1)若函數(shù) 在其定義域內(nèi)為單調(diào)遞增函數(shù),求實(shí)數(shù)
在其定義域內(nèi)為單調(diào)遞增函數(shù),求實(shí)數(shù) 的取值范圍。
的取值范圍。
(2)若函數(shù) ,若在[1,e]上至少存在一個(gè)x的值使
,若在[1,e]上至少存在一個(gè)x的值使 成立,求實(shí)數(shù)
成立,求實(shí)數(shù) 的取值范圍。
的取值范圍。
【解析】第一問中,利用導(dǎo)數(shù) ,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911301664012899/SYS201207091131067338626240_ST.files/image003.png">在其定義域內(nèi)的單調(diào)遞增函數(shù),所以
,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911301664012899/SYS201207091131067338626240_ST.files/image003.png">在其定義域內(nèi)的單調(diào)遞增函數(shù),所以 內(nèi)滿足
內(nèi)滿足 恒成立,得到結(jié)論第二問中,在[1,e]上至少存在一個(gè)x的值使
恒成立,得到結(jié)論第二問中,在[1,e]上至少存在一個(gè)x的值使 成立,等價(jià)于不等式
成立,等價(jià)于不等式 在[1,e]上有解,轉(zhuǎn)換為不等式有解來(lái)解答即可。
在[1,e]上有解,轉(zhuǎn)換為不等式有解來(lái)解答即可。
解:(1) ,
,
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911301664012899/SYS201207091131067338626240_ST.files/image003.png">在其定義域內(nèi)的單調(diào)遞增函數(shù),
所以 內(nèi)滿足
內(nèi)滿足 恒成立,即
恒成立,即 恒成立,
恒成立,
亦即 ,
,
 即可 又
即可 又
當(dāng)且僅當(dāng) ,即x=1時(shí)取等號(hào),
,即x=1時(shí)取等號(hào),
 在其定義域內(nèi)為單調(diào)增函數(shù)的實(shí)數(shù)k的取值范圍是
在其定義域內(nèi)為單調(diào)增函數(shù)的實(shí)數(shù)k的取值范圍是 .
.
(2)在[1,e]上至少存在一個(gè)x的值使 成立,等價(jià)于不等式
成立,等價(jià)于不等式 在[1,e]上有解,設(shè)
在[1,e]上有解,設(shè)

 上的增函數(shù),
上的增函數(shù), 依題意需
依題意需
 實(shí)數(shù)k的取值范圍是
實(shí)數(shù)k的取值范圍是
設(shè)函數(shù)f(x)= 在[1,+∞
在[1,+∞ 上為增函數(shù).
上為增函數(shù).
(1)求正實(shí)數(shù)a的取值范圍;
(2)比較 的大小,說明理由;
的大小,說明理由;
(3)求證: (n∈N*, n≥2)
(n∈N*, n≥2)
【解析】第一問中,利用
解:(1)由已知: ,依題意得:
,依題意得: ≥0對(duì)x∈[1,+∞
≥0對(duì)x∈[1,+∞ 恒成立
恒成立
∴ax-1≥0對(duì)x∈[1,+∞ 恒成立 ∴a-1≥0即:a≥1
恒成立 ∴a-1≥0即:a≥1
(2)∵a=1 ∴由(1)知:f(x)= 在[1,+∞)上為增函數(shù),
在[1,+∞)上為增函數(shù),
∴n≥2時(shí):f( )=
)=
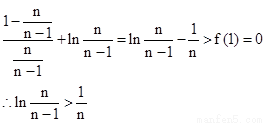
(3) ∵ ∴
∴
一支車隊(duì)有15輛車,某天依次出發(fā)執(zhí)行運(yùn)輸任務(wù),第一輛車于下午2時(shí)出發(fā),第二輛車于下午2時(shí)10分出發(fā),第三輛車于下午2時(shí)20分出發(fā),依此類推。假設(shè)所有的司機(jī)都連續(xù)開車,并都在下午6時(shí)停下來(lái)休息。
(1)到下午6時(shí)最后一輛車行駛了多長(zhǎng)時(shí)間?
(2)如果每輛車的行駛速度都是60 ,這個(gè)車隊(duì)當(dāng)天一共行駛了多少千米?
,這個(gè)車隊(duì)當(dāng)天一共行駛了多少千米?
【解析】第一問中,利用第一輛車出發(fā)時(shí)間為下午2時(shí),每隔10分鐘即 小時(shí)出發(fā)一輛
小時(shí)出發(fā)一輛
則第15輛車在 小時(shí),最后一輛車出發(fā)時(shí)間為:
小時(shí),最后一輛車出發(fā)時(shí)間為: 小時(shí)
小時(shí)
第15輛車行駛時(shí)間為: 小時(shí)(1時(shí)40分)
小時(shí)(1時(shí)40分)
第二問中,設(shè)每輛車行駛的時(shí)間為: ,由題意得到
,由題意得到
 是以
是以 為首項(xiàng),
為首項(xiàng), 為公差的等差數(shù)列
為公差的等差數(shù)列
則行駛的總時(shí)間為:
則行駛的總里程為: 運(yùn)用等差數(shù)列求和得到。
運(yùn)用等差數(shù)列求和得到。
解:(1)第一輛車出發(fā)時(shí)間為下午2時(shí),每隔10分鐘即 小時(shí)出發(fā)一輛
小時(shí)出發(fā)一輛
則第15輛車在 小時(shí),最后一輛車出發(fā)時(shí)間為:
小時(shí),最后一輛車出發(fā)時(shí)間為: 小時(shí)
小時(shí)
第15輛車行駛時(shí)間為: 小時(shí)(1時(shí)40分)
……5分
小時(shí)(1時(shí)40分)
……5分
(2)設(shè)每輛車行駛的時(shí)間為: ,由題意得到
,由題意得到
 是以
是以 為首項(xiàng),
為首項(xiàng), 為公差的等差數(shù)列
為公差的等差數(shù)列
則行駛的總時(shí)間為: ……10分
……10分
則行駛的總里程為:
一自來(lái)水廠用蓄水池通過管道向所管轄區(qū)域供水.某日凌晨,已知蓄水池有水9千噸,水廠計(jì)劃在當(dāng)日每小時(shí)向蓄水池注入水2千噸,且每 小時(shí)通過管道向所管轄區(qū)域供水
小時(shí)通過管道向所管轄區(qū)域供水 千噸.
千噸.
(1)多少小時(shí)后,蓄水池存水量最少?
(2)當(dāng)蓄水池存水量少于3千噸時(shí),供水就會(huì)出現(xiàn)緊張現(xiàn)象,那么當(dāng)日出現(xiàn)這種情況的時(shí)間有多長(zhǎng)?
【解析】第一問中(1)設(shè) 小時(shí)后,蓄水池有水
小時(shí)后,蓄水池有水 千噸.依題意,
千噸.依題意, 當(dāng)
當(dāng) ,即
,即 (小時(shí))時(shí),蓄水池的水量最少,只有1千噸
(小時(shí))時(shí),蓄水池的水量最少,只有1千噸
第二問依題意, 解得:
解得:
解:(1)設(shè) 小時(shí)后,蓄水池有水
小時(shí)后,蓄水池有水 千噸.………………………………………1分
千噸.………………………………………1分
依題意, …………………………………………4分
…………………………………………4分
當(dāng) ,即
,即 (小時(shí))時(shí),蓄水池的水量最少,只有1千噸. ………2分
(小時(shí))時(shí),蓄水池的水量最少,只有1千噸. ………2分
(2)依題意, ………………………………………………3分
………………………………………………3分
解得: . …………………………………………………………………3分
. …………………………………………………………………3分
所以,當(dāng)天有8小時(shí)會(huì)出現(xiàn)供水緊張的情況
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com