
題目列表(包括答案和解析)
(12分)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() (
(![]() 為正整數)
為正整數)
(I)求數列![]() 的通項公式;
的通項公式;
已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且對任意正整數
,且對任意正整數![]() ,有
,有![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() )成等差數列,令
)成等差數列,令![]() 。
。
(1)求數列![]() 的通項公式
的通項公式![]() (用
(用![]() ,
,![]() 表示)
表示)
(2)當![]() 時,數列
時,數列![]() 是否存在最小項,若有,請求出第幾項最小;若無,請說明理由;
是否存在最小項,若有,請求出第幾項最小;若無,請說明理由;
(3)若![]() 是一個單調遞增數列,請求出
是一個單調遞增數列,請求出![]() 的取值范圍。
的取值范圍。
已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,
,
(Ⅰ)求![]() ,
,![]() ,
, ![]() ,并猜想
,并猜想![]() 的表達式;
的表達式;
(Ⅱ)用數學歸納法證明所得的結論。
已知數列![]() 的前
的前![]()
![]() 項和為
項和為![]() ,且
,且![]() ,
,![]()
(1)證明:![]() 是等比數列;
是等比數列;
(2)求數列![]() 的通項公式,并求出n為何值時,
的通項公式,并求出n為何值時,![]() 取得最小值,并說明理由。
取得最小值,并說明理由。
(2)![]() =
=![]() n=15取得最小值
n=15取得最小值
(12分)已知數列 的前
的前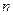 項和為
項和為 ,且滿足
,且滿足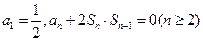 。
。
(1)問:數列 是否為等差數列?并證明你的結論;
是否為等差數列?并證明你的結論;
(2)求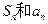 ;
;
(3)求證: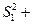
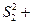
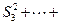
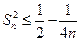 。
。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com