
題目列表(包括答案和解析)
已知函數(shù)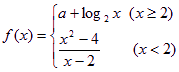 在點(diǎn)
在點(diǎn)![]() 處連續(xù),則常數(shù)
處連續(xù),則常數(shù)![]() 的值是
的值是
A.2 B.3 C.4 D.5
已知函數(shù)![]() 在R上滿足
在R上滿足![]() ,則曲線
,則曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程是
處的切線方程是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(本題13分)已知函數(shù)![]()
(1)已知一直線![]() 經(jīng)過原點(diǎn)
經(jīng)過原點(diǎn)![]() 且與曲線
且與曲線![]() 相切,求
相切,求![]() 的直線方程;
的直線方程;
(2)若關(guān)于![]() 的方程
的方程![]() 有兩個不等的實(shí)根,求實(shí)數(shù)
有兩個不等的實(shí)根,求實(shí)數(shù)![]() 的取值范圍。
的取值范圍。
(本題12分)定義在R上的函數(shù)![]() ,已知
,已知![]() 在
在![]() 上有最小值3。
上有最小值3。
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)求![]() 在
在![]() 上的最大值。
上的最大值。
(本題12分)已知某種從太空帶回的植物種子每粒成功發(fā)芽的概率都為![]() ,某植物研究所分兩個小組分別獨(dú)立開展該種子的發(fā)芽實(shí)驗(yàn),每次實(shí)驗(yàn)種一粒種子,假定某次實(shí)驗(yàn)種子發(fā)芽則稱該次實(shí)驗(yàn)是成功的,如果種子沒有發(fā)芽,則稱該次實(shí)驗(yàn)是失敗的.
,某植物研究所分兩個小組分別獨(dú)立開展該種子的發(fā)芽實(shí)驗(yàn),每次實(shí)驗(yàn)種一粒種子,假定某次實(shí)驗(yàn)種子發(fā)芽則稱該次實(shí)驗(yàn)是成功的,如果種子沒有發(fā)芽,則稱該次實(shí)驗(yàn)是失敗的.
(1) 第一小組做了三次實(shí)驗(yàn),求實(shí)驗(yàn)成功的平均次數(shù);
(2) 第二小組連續(xù)進(jìn)行實(shí)驗(yàn),求實(shí)驗(yàn)首次成功時所需的實(shí)驗(yàn)次數(shù)的期望;
(3)兩個小組分別進(jìn)行2次試驗(yàn),求至少有2次實(shí)驗(yàn)成功的概率.
1.解析:學(xué)(理科)卷.files/image324.gif) ,故選A。
,故選A。
2.解析:∵學(xué)(理科)卷.files/image012.gif)
學(xué)(理科)卷.files/image326.gif) ,
,
故選B。
3.解析:由學(xué)(理科)卷.files/image328.gif) ,得
,得學(xué)(理科)卷.files/image330.gif) ,此時
,此時學(xué)(理科)卷.files/image332.gif) ,所以,
,所以,學(xué)(理科)卷.files/image334.gif) ,故選C。
,故選C。
4.解析:顯然,若學(xué)(理科)卷.files/image044.gif) 與
與學(xué)(理科)卷.files/image046.gif) 共線,則
共線,則學(xué)(理科)卷.files/image048.gif) 與
與學(xué)(理科)卷.files/image050.gif) 共線;若
共線;若學(xué)(理科)卷.files/image048.gif) 與
與學(xué)(理科)卷.files/image050.gif) 共線,則
共線,則學(xué)(理科)卷.files/image336.gif) ,即
,即學(xué)(理科)卷.files/image338.gif)
學(xué)(理科)卷.files/image340.gif) ,得
,得學(xué)(理科)卷.files/image342.gif) ,∴
,∴學(xué)(理科)卷.files/image044.gif) 與
與學(xué)(理科)卷.files/image046.gif) 共線,∴
共線,∴學(xué)(理科)卷.files/image044.gif) 與
與學(xué)(理科)卷.files/image046.gif) 共線是
共線是學(xué)(理科)卷.files/image048.gif) 與
與學(xué)(理科)卷.files/image050.gif) 共線的充要條件,故選C。
共線的充要條件,故選C。
5.解析:設(shè)公差為學(xué)(理科)卷.files/image344.gif) ,由題意得,
,由題意得,學(xué)(理科)卷.files/image346.gif) ;
;學(xué)(理科)卷.files/image348.gif) ,解得
,解得學(xué)(理科)卷.files/image056.gif) 或
或學(xué)(理科)卷.files/image058.gif) ,故選C。
,故選C。
6.解析:∵雙曲線學(xué)(理科)卷.files/image064.gif) 的右焦點(diǎn)到一條漸近線的距離等于焦距的
的右焦點(diǎn)到一條漸近線的距離等于焦距的學(xué)(理科)卷.files/image066.gif) ,∴
,∴學(xué)(理科)卷.files/image351.gif) ,又∵
,又∵學(xué)(理科)卷.files/image353.gif) ,∴
,∴學(xué)(理科)卷.files/image355.gif) ,∴
,∴學(xué)(理科)卷.files/image357.gif) ,∴雙曲線的離心率是
,∴雙曲線的離心率是學(xué)(理科)卷.files/image069.gif) 。故選B.
。故選B.
7.解析:∵學(xué)(理科)卷.files/image074.gif) 、
、學(xué)(理科)卷.files/image076.gif) 為正實(shí)數(shù),∴
為正實(shí)數(shù),∴學(xué)(理科)卷.files/image359.gif) ,∴
,∴學(xué)(理科)卷.files/image078.gif) ;由均值不等式得
;由均值不等式得學(xué)(理科)卷.files/image082.gif) 恒成立,
恒成立,學(xué)(理科)卷.files/image361.gif) ,故②不恒成立,又因?yàn)楹瘮?shù)
,故②不恒成立,又因?yàn)楹瘮?shù)學(xué)(理科)卷.files/image363.gif) 在
在學(xué)(理科)卷.files/image365.gif) 是增函數(shù),∴
是增函數(shù),∴學(xué)(理科)卷.files/image084.gif) ,故恒成立的不等式是①③④。故選C.
,故恒成立的不等式是①③④。故選C.
8.解析:∵學(xué)(理科)卷.files/image367.gif) ,∴
,∴學(xué)(理科)卷.files/image369.gif) 在區(qū)間
在區(qū)間學(xué)(理科)卷.files/image092.gif) 上恒成立,即
上恒成立,即學(xué)(理科)卷.files/image371.gif) 在區(qū)間
在區(qū)間學(xué)(理科)卷.files/image092.gif) 上恒成立,∴
上恒成立,∴學(xué)(理科)卷.files/image373.gif) ,故選D。
,故選D。
9.解析:∵學(xué)(理科)卷.files/image104.gif)
學(xué)(理科)卷.files/image376.gif)
學(xué)(理科)卷.files/image378.gif) ,此函數(shù)的最小值為
,此函數(shù)的最小值為學(xué)(理科)卷.files/image107.gif) ,故選C。
,故選C。
10.解析:如圖,∵正三角形學(xué)(理科)卷.files/image117.gif) 的邊長為
的邊長為學(xué)(理科)卷.files/image113.gif) ,∴
,∴學(xué)(理科)卷.files/image380.gif) ,∴
,∴學(xué)(理科)卷.files/image382.gif) ,又∵
,又∵學(xué)(理科)卷.files/image384.gif) ,∴
,∴學(xué)(理科)卷.files/image386.gif) ,故選D。
,故選D。
11.解析:∵學(xué)(理科)卷.files/image134.gif) 在區(qū)間
在區(qū)間學(xué)(理科)卷.files/image388.gif) 上是增函數(shù)且
上是增函數(shù)且學(xué)(理科)卷.files/image390.gif) ,∴其反函數(shù)
,∴其反函數(shù)學(xué)(理科)卷.files/image132.gif) 在區(qū)間上
在區(qū)間上學(xué)(理科)卷.files/image392.gif) 是增函數(shù),∴
是增函數(shù),∴學(xué)(理科)卷.files/image138.gif)
學(xué)(理科)卷.files/image142.gif)
學(xué)(理科)卷.files/image140.gif) ,故選A
,故選A
12.解析:如圖,①當(dāng)學(xué)(理科)卷.files/image394.gif) 或
或學(xué)(理科)卷.files/image396.gif) 時,圓面
時,圓面學(xué)(理科)卷.files/image154.gif) 被分成2塊,涂色方法有20種;②當(dāng)
被分成2塊,涂色方法有20種;②當(dāng)學(xué)(理科)卷.files/image398.gif) 或
或學(xué)(理科)卷.files/image400.gif) 時,圓面
時,圓面學(xué)(理科)卷.files/image154.gif) 被分成3塊,涂色方法有60種;
被分成3塊,涂色方法有60種;
③當(dāng)學(xué)(理科)卷.files/image402.gif) 時,圓面
時,圓面學(xué)(理科)卷.files/image154.gif) 被分成4塊,涂色方法有120種,所以m的取值范圍是
被分成4塊,涂色方法有120種,所以m的取值范圍是學(xué)(理科)卷.files/image156.gif) ,故選A。
,故選A。
13.解析:做出學(xué)(理科)卷.files/image168.gif) 表示的平面區(qū)域如圖,當(dāng)直線
表示的平面區(qū)域如圖,當(dāng)直線學(xué)(理科)卷.files/image284.gif) 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)學(xué)(理科)卷.files/image405.gif) 時,
時,學(xué)(理科)卷.files/image170.gif) 取得最大值5。
取得最大值5。
學(xué)(理科)卷.files/image407.gif) 14.解析:∵
14.解析:∵學(xué)(理科)卷.files/image409.gif) ,∴
,∴學(xué)(理科)卷.files/image411.gif) 時,
時,學(xué)(理科)卷.files/image413.gif) ,又
,又學(xué)(理科)卷.files/image415.gif) 時,
時,學(xué)(理科)卷.files/image417.gif) 滿足上式,因此,
滿足上式,因此,學(xué)(理科)卷.files/image419.gif) ,
,
∴學(xué)(理科)卷.files/image421.gif) 。
。
學(xué)(理科)卷.files/image423.gif) 15.解析:設(shè)正四面體的棱長為
15.解析:設(shè)正四面體的棱長為學(xué)(理科)卷.files/image074.gif) ,連
,連學(xué)(理科)卷.files/image426.gif) ,取
,取學(xué)(理科)卷.files/image426.gif) 的中點(diǎn)
的中點(diǎn)學(xué)(理科)卷.files/image429.gif) ,連
,連學(xué)(理科)卷.files/image431.gif) ,∵
,∵學(xué)(理科)卷.files/image188.gif) 為
為學(xué)(理科)卷.files/image190.gif) 的中點(diǎn),∴
的中點(diǎn),∴學(xué)(理科)卷.files/image185.gif) ∥
∥學(xué)(理科)卷.files/image431.gif) ,∴
,∴學(xué)(理科)卷.files/image435.gif) 或其補(bǔ)角為
或其補(bǔ)角為學(xué)(理科)卷.files/image185.gif) 與
與學(xué)(理科)卷.files/image193.gif) 所成角,∵
所成角,∵學(xué)(理科)卷.files/image437.gif) ,
,學(xué)(理科)卷.files/image439.gif) ,∴
,∴學(xué)(理科)卷.files/image441.gif) ,∴
,∴學(xué)(理科)卷.files/image443.gif) ,又∵
,又∵學(xué)(理科)卷.files/image445.gif) ,∴
,∴學(xué)(理科)卷.files/image447.gif) ,∴
,∴學(xué)(理科)卷.files/image185.gif) 與
與學(xué)(理科)卷.files/image193.gif) 所成角的余弦值為
所成角的余弦值為學(xué)(理科)卷.files/image449.gif) 。
。
學(xué)(理科)卷.files/image451.jpg) 16.解析:∵
16.解析:∵學(xué)(理科)卷.files/image205.gif) ,∴
,∴學(xué)(理科)卷.files/image453.gif) ,∵點(diǎn)
,∵點(diǎn)學(xué)(理科)卷.files/image195.gif) 為
為學(xué)(理科)卷.files/image197.gif) 的準(zhǔn)線與
的準(zhǔn)線與學(xué)(理科)卷.files/image199.gif) 軸的交點(diǎn),由向量的加法法則及拋物線的對稱性可知,點(diǎn)
軸的交點(diǎn),由向量的加法法則及拋物線的對稱性可知,點(diǎn)學(xué)(理科)卷.files/image203.gif) 為拋物線上關(guān)于軸對稱的兩點(diǎn)且做出圖形如右圖,其中
為拋物線上關(guān)于軸對稱的兩點(diǎn)且做出圖形如右圖,其中學(xué)(理科)卷.files/image455.gif) 為點(diǎn)
為點(diǎn)學(xué)(理科)卷.files/image295.gif) 到準(zhǔn)線的距離,四邊形
到準(zhǔn)線的距離,四邊形學(xué)(理科)卷.files/image458.gif) 為菱形,∴
為菱形,∴學(xué)(理科)卷.files/image460.gif) ,∴
,∴學(xué)(理科)卷.files/image462.gif) ,∴
,∴學(xué)(理科)卷.files/image464.gif) ,∴
,∴學(xué)(理科)卷.files/image466.gif) ,∴
,∴學(xué)(理科)卷.files/image468.gif) ,∴向量
,∴向量學(xué)(理科)卷.files/image207.gif) 與
與學(xué)(理科)卷.files/image209.gif) 的夾角為
的夾角為學(xué)(理科)卷.files/image470.gif) 。
。
17.(10分)解析:(Ⅰ)由正弦定理得,學(xué)(理科)卷.files/image472.gif) ,
,學(xué)(理科)卷.files/image474.gif) ,…2分
,…2分
∴學(xué)(理科)卷.files/image476.gif) ,
,學(xué)(理科)卷.files/image478.gif) ,………4分
,………4分
(Ⅱ)∵學(xué)(理科)卷.files/image217.gif) ,
,學(xué)(理科)卷.files/image219.gif) ,∴
,∴學(xué)(理科)卷.files/image480.gif) ,∴
,∴學(xué)(理科)卷.files/image482.gif) ,………………………6分
,………………………6分
又∵學(xué)(理科)卷.files/image225.gif) ,∴
,∴學(xué)(理科)卷.files/image484.gif) ,∴
,∴學(xué)(理科)卷.files/image486.gif) ,………………………8分
,………………………8分
∴學(xué)(理科)卷.files/image488.gif) 。………………………10分
。………………………10分
18.解析:(Ⅰ)∵學(xué)(理科)卷.files/image490.gif) ,∴
,∴學(xué)(理科)卷.files/image492.gif) ;……………………理3文4分
;……………………理3文4分
(Ⅱ)∵三科會考不合格的概率均為學(xué)(理科)卷.files/image494.gif) ,∴學(xué)生甲不能拿到高中畢業(yè)證的概率
,∴學(xué)生甲不能拿到高中畢業(yè)證的概率學(xué)(理科)卷.files/image496.gif) ;……………………理6文8分
;……………………理6文8分
(Ⅲ)∵每科得A,B的概率分別為學(xué)(理科)卷.files/image498.gif) ,∴學(xué)生甲被評為三好學(xué)生的概率為
,∴學(xué)生甲被評為三好學(xué)生的概率為學(xué)(理科)卷.files/image500.gif) 。……………………12分
。……………………12分
(理)∵學(xué)(理科)卷.files/image502.gif)
學(xué)(理科)卷.files/image504.gif) ,
,學(xué)(理科)卷.files/image506.gif) ,
,學(xué)(理科)卷.files/image508.gif) ,
,學(xué)(理科)卷.files/image510.gif) 。……………………9分
。……………………9分
∴學(xué)(理科)卷.files/image232.gif) 的分布列如下表:
的分布列如下表:
學(xué)(理科)卷.files/image232.gif)
0
1
2
3
學(xué)(理科)卷.files/image513.gif)
學(xué)(理科)卷.files/image515.gif)
學(xué)(理科)卷.files/image517.gif)
學(xué)(理科)卷.files/image519.gif)
學(xué)(理科)卷.files/image521.gif)
∴學(xué)(理科)卷.files/image232.gif) 的數(shù)學(xué)期望
的數(shù)學(xué)期望學(xué)(理科)卷.files/image235.gif)
學(xué)(理科)卷.files/image523.gif) 。……………………12分
。……………………12分
19.(12分)解析:(Ⅰ)學(xué)(理科)卷.files/image240.gif) 時,
時,
學(xué)(理科)卷.files/image526.gif) ,
,學(xué)(理科)卷.files/image528.gif)
學(xué)(理科)卷.files/image530.gif) ,
,
學(xué)(理科)卷.files/image532.gif)
學(xué)(理科)卷.files/image534.gif)
由學(xué)(理科)卷.files/image536.gif) 得,
得,學(xué)(理科)卷.files/image538.gif) 或
或學(xué)(理科)卷.files/image540.gif) ………3分
………3分
學(xué)(理科)卷.files/image199.gif)
學(xué)(理科)卷.files/image543.gif)
學(xué)(理科)卷.files/image545.gif)
學(xué)(理科)卷.files/image547.gif)
學(xué)(理科)卷.files/image549.gif)
學(xué)(理科)卷.files/image551.gif)
學(xué)(理科)卷.files/image553.gif)
+
0
-
0
+
學(xué)(理科)卷.files/image555.gif)
遞增
極大值學(xué)(理科)卷.files/image557.gif)
遞減
極小值學(xué)(理科)卷.files/image559.gif)
遞增
學(xué)(理科)卷.files/image561.gif) ,
,學(xué)(理科)卷.files/image563.gif) ………………………6分
………………………6分
(Ⅱ)學(xué)(理科)卷.files/image565.gif) 在定義域
在定義域學(xué)(理科)卷.files/image567.gif) 上是增函數(shù),
上是增函數(shù),
學(xué)(理科)卷.files/image528.gif)
學(xué)(理科)卷.files/image570.gif) 對
對學(xué)(理科)卷.files/image572.gif) 恒成立,即
恒成立,即學(xué)(理科)卷.files/image574.gif)
學(xué)(理科)卷.files/image576.gif) ………………………9分
………………………9分
又學(xué)(理科)卷.files/image578.gif) (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng)學(xué)(理科)卷.files/image580.gif) 時,
時,學(xué)(理科)卷.files/image582.gif) )
)
學(xué)(理科)卷.files/image584.gif)
學(xué)(理科)卷.files/image586.gif) ………………………4分
………………………4分
學(xué)(理科)卷.files/image588.gif)
20.解析:(Ⅰ)∵學(xué)(理科)卷.files/image254.gif) ∥
∥學(xué)(理科)卷.files/image256.gif) ,
,學(xué)(理科)卷.files/image258.gif) ,∴
,∴學(xué)(理科)卷.files/image590.gif) ,∵
,∵學(xué)(理科)卷.files/image251.gif) 底面
底面學(xué)(理科)卷.files/image249.gif) ,∴
,∴學(xué)(理科)卷.files/image592.gif) ,∴
,∴學(xué)(理科)卷.files/image594.gif) 平面
平面學(xué)(理科)卷.files/image596.gif) ,∴
,∴學(xué)(理科)卷.files/image598.gif) ,又∵
,又∵學(xué)(理科)卷.files/image269.gif) 平面
平面學(xué)(理科)卷.files/image271.gif) ,∴
,∴學(xué)(理科)卷.files/image600.gif) ,∴
,∴學(xué)(理科)卷.files/image602.gif) 平面
平面學(xué)(理科)卷.files/image604.gif) ,∴
,∴學(xué)(理科)卷.files/image273.gif) 。………………………4分
。………………………4分
(Ⅱ)∵學(xué)(理科)卷.files/image602.gif) 平面
平面學(xué)(理科)卷.files/image604.gif) ,∴
,∴學(xué)(理科)卷.files/image606.gif) ,
,學(xué)(理科)卷.files/image608.gif) ,∴
,∴學(xué)(理科)卷.files/image610.gif) 為二面角
為二面角學(xué)(理科)卷.files/image275.gif) 的平面角,………………………6分
的平面角,………………………6分
學(xué)(理科)卷.files/image612.gif) ,
,學(xué)(理科)卷.files/image614.gif) ,∴
,∴學(xué)(理科)卷.files/image616.gif) ,又∵
,又∵學(xué)(理科)卷.files/image594.gif) 平面
平面學(xué)(理科)卷.files/image596.gif) ,
,學(xué)(理科)卷.files/image618.gif) ,∴
,∴學(xué)(理科)卷.files/image620.gif) ,∴二面角
,∴二面角學(xué)(理科)卷.files/image275.gif) 的正切值的大小為
的正切值的大小為學(xué)(理科)卷.files/image622.gif) 。………………………8分
。………………………8分
(Ⅲ)過點(diǎn)學(xué)(理科)卷.files/image262.gif) 做
做學(xué)(理科)卷.files/image625.gif) ∥
∥學(xué)(理科)卷.files/image256.gif) ,交
,交學(xué)(理科)卷.files/image190.gif) 于點(diǎn)
于點(diǎn)學(xué)(理科)卷.files/image429.gif) ,∵
,∵學(xué)(理科)卷.files/image269.gif) 平面
平面學(xué)(理科)卷.files/image271.gif) ,∴
,∴學(xué)(理科)卷.files/image630.gif) 為
為學(xué)(理科)卷.files/image625.gif) 在平面
在平面學(xué)(理科)卷.files/image271.gif) 內(nèi)的射影,∴
內(nèi)的射影,∴學(xué)(理科)卷.files/image632.gif) 為
為學(xué)(理科)卷.files/image625.gif) 與平面
與平面學(xué)(理科)卷.files/image271.gif) 所成的角,………………………10分
所成的角,………………………10分
學(xué)(理科)卷.files/image634.gif) ∵
∵學(xué)(理科)卷.files/image636.gif) ,∴
,∴學(xué)(理科)卷.files/image638.gif) ,又∵
,又∵學(xué)(理科)卷.files/image625.gif) ∥
∥學(xué)(理科)卷.files/image256.gif) ,∴
,∴學(xué)(理科)卷.files/image625.gif) 和
和學(xué)(理科)卷.files/image256.gif) 與平面
與平面學(xué)(理科)卷.files/image271.gif) 所成的角相等,∴
所成的角相等,∴學(xué)(理科)卷.files/image256.gif) 與平面
與平面學(xué)(理科)卷.files/image271.gif) 所成角的正切值為
所成角的正切值為學(xué)(理科)卷.files/image640.gif) 。………………………12分
。………………………12分
解法2:如圖建立空間直角坐標(biāo)系,(Ⅰ)∵,學(xué)(理科)卷.files/image260.gif) ,∴點(diǎn)
,∴點(diǎn)學(xué)(理科)卷.files/image642.gif) 的坐標(biāo)分別是
的坐標(biāo)分別是學(xué)(理科)卷.files/image644.gif) ,
,學(xué)(理科)卷.files/image646.gif) ,
,學(xué)(理科)卷.files/image648.gif)
學(xué)(理科)卷.files/image650.gif) ,∴
,∴學(xué)(理科)卷.files/image652.gif) ,
,學(xué)(理科)卷.files/image654.gif) ,設(shè)
,設(shè)學(xué)(理科)卷.files/image656.gif) ,∵
,∵學(xué)(理科)卷.files/image269.gif) 平面
平面學(xué)(理科)卷.files/image271.gif) ,∴
,∴學(xué)(理科)卷.files/image658.gif) ,∴
,∴學(xué)(理科)卷.files/image660.gif) ,取
,取學(xué)(理科)卷.files/image662.gif) ,∴
,∴學(xué)(理科)卷.files/image664.gif) ,∴
,∴學(xué)(理科)卷.files/image273.gif) 。………………………4分
。………………………4分
(Ⅱ)設(shè)二面角學(xué)(理科)卷.files/image275.gif) 的大小為
的大小為學(xué)(理科)卷.files/image666.gif) ,∵平面
,∵平面學(xué)(理科)卷.files/image271.gif) 的法向量是
的法向量是學(xué)(理科)卷.files/image652.gif) ,平面
,平面學(xué)(理科)卷.files/image669.gif) 的法向量是
的法向量是學(xué)(理科)卷.files/image671.gif) ,∴
,∴學(xué)(理科)卷.files/image673.gif) ,∴
,∴學(xué)(理科)卷.files/image675.gif) ,∴二面角
,∴二面角學(xué)(理科)卷.files/image275.gif) 的正切值的大小為
的正切值的大小為學(xué)(理科)卷.files/image622.gif) 。………………………8分
。………………………8分
(Ⅲ)設(shè)學(xué)(理科)卷.files/image256.gif) 與平面
與平面學(xué)(理科)卷.files/image271.gif) 所成角的大小為
所成角的大小為學(xué)(理科)卷.files/image666.gif) ,∵平面
,∵平面學(xué)(理科)卷.files/image271.gif) 的法向量是
的法向量是學(xué)(理科)卷.files/image678.gif) ,
,學(xué)(理科)卷.files/image680.gif) ,∴
,∴學(xué)(理科)卷.files/image682.gif) ,∴
,∴學(xué)(理科)卷.files/image684.gif) ,∴
,∴學(xué)(理科)卷.files/image256.gif) 與平面
與平面學(xué)(理科)卷.files/image271.gif) 所成角的正切值為
所成角的正切值為學(xué)(理科)卷.files/image640.gif) 。………………………12分
。………………………12分
21.(Ⅰ) 解析:如圖,設(shè)右準(zhǔn)線學(xué)(理科)卷.files/image686.gif) 與
與學(xué)(理科)卷.files/image199.gif) 軸的交點(diǎn)為
軸的交點(diǎn)為學(xué)(理科)卷.files/image689.gif) ,過點(diǎn)
,過點(diǎn)學(xué)(理科)卷.files/image262.gif)
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com