
題目列表(包括答案和解析)
已知函數(shù) (
( 為實(shí)數(shù)).
為實(shí)數(shù)).
(Ⅰ)當(dāng) 時(shí),求
時(shí),求 的最小值;
的最小值;
(Ⅱ)若 在
在 上是單調(diào)函數(shù),求
上是單調(diào)函數(shù),求 的取值范圍.
的取值范圍.
【解析】第一問中由題意可知: . ∵
. ∵ ∴
∴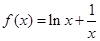 ∴
∴
 .
.
當(dāng) 時(shí),
時(shí), ;
當(dāng)
;
當(dāng) 時(shí),
時(shí), . 故
. 故 .
.
第二問
 .
.
當(dāng) 時(shí),
時(shí), ,在
,在 上有
上有 ,
, 遞增,符合題意;
遞增,符合題意;
令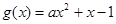 ,則
,則
 ,∴
,∴ 或
或 在
在 上恒成立.轉(zhuǎn)化后解決最值即可。
上恒成立.轉(zhuǎn)化后解決最值即可。
解:(Ⅰ) 由題意可知: . ∵
. ∵ ∴
∴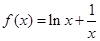 ∴
∴
 .
.
當(dāng) 時(shí),
時(shí), ;
當(dāng)
;
當(dāng) 時(shí),
時(shí), . 故
. 故 .
.
(Ⅱ) 
 .
.
當(dāng) 時(shí),
時(shí), ,在
,在 上有
上有 ,
, 遞增,符合題意;
遞增,符合題意;
令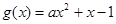 ,則
,則
 ,∴
,∴ 或
或 在
在 上恒成立.∵二次函數(shù)
上恒成立.∵二次函數(shù)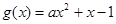 的對稱軸為
的對稱軸為 ,且
,且
∴ 或
或
 或
或
 或
或
 或
或 . 綜上
. 綜上
心理學(xué)家研究發(fā)現(xiàn):一般情況下,學(xué)生的注意力隨著老師講課時(shí)間的變化而變化.講課開始時(shí),學(xué)生的注意力逐步增強(qiáng),中間有一段時(shí)間學(xué)生的注意力保持較為理想的狀態(tài),隨后學(xué)生的注意力開始分散.經(jīng)過實(shí)驗(yàn)分析可知,學(xué)生的注意力y隨時(shí)間t的變化規(guī)律有如下關(guān)系式:
y=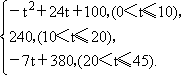
(1)講課開始后第5分鐘時(shí)與講課開始后第25分鐘時(shí)比較,何時(shí)學(xué)生的注意力更集中?
(2)講課開始后多少分鐘,學(xué)生的注意力最集中?能持續(xù)多少分鐘?
(3)一道數(shù)學(xué)綜合題,需要講解24分鐘,為了效果較好,要求學(xué)生的注意力最低達(dá)到180,那么經(jīng)過適當(dāng)安排,老師能否在學(xué)生注意力達(dá)到所需的狀態(tài)下講解完這道題目?如果不能講解完,說明理由;如果能夠講解完,請說明老師應(yīng)該在哪個(gè)時(shí)間段內(nèi)講解.
已知函數(shù) ,數(shù)列
,數(shù)列 的項(xiàng)滿足:
的項(xiàng)滿足: ,(1)試求
,(1)試求
(2) 猜想數(shù)列 的通項(xiàng),并利用數(shù)學(xué)歸納法證明.
的通項(xiàng),并利用數(shù)學(xué)歸納法證明.
【解析】第一問中,利用遞推關(guān)系 ,
, 
 ,
, 
第二問中,由(1)猜想得: 然后再用數(shù)學(xué)歸納法分為兩步驟證明即可。
然后再用數(shù)學(xué)歸納法分為兩步驟證明即可。
解: (1)  ,
,

 ,
,  …………….7分
…………….7分
(2)由(1)猜想得:
(數(shù)學(xué)歸納法證明)i)  ,
,
 ,命題成立
,命題成立
ii) 假設(shè) 時(shí),
時(shí), 成立
成立
則 時(shí),
時(shí),


綜合i),ii) :  成立
成立
函數(shù) 是定義在
是定義在 上的奇函數(shù),且
上的奇函數(shù),且 。
。
(1)求實(shí)數(shù)a,b,并確定函數(shù) 的解析式;
的解析式;
(2)判斷 在(-1,1)上的單調(diào)性,并用定義證明你的結(jié)論;
在(-1,1)上的單調(diào)性,并用定義證明你的結(jié)論;
(3)寫出 的單調(diào)減區(qū)間,并判斷
的單調(diào)減區(qū)間,并判斷 有無最大值或最小值?如有,寫出最大值或最小值。(本小問不需要說明理由)
有無最大值或最小值?如有,寫出最大值或最小值。(本小問不需要說明理由)
【解析】本試題主要考查了函數(shù)的解析式和奇偶性和單調(diào)性的綜合運(yùn)用。第一問中,利用函數(shù) 是定義在
是定義在 上的奇函數(shù),且
上的奇函數(shù),且 。
。
解得 ,
,
(2)中,利用單調(diào)性的定義,作差變形判定可得單調(diào)遞增函數(shù)。
(3)中,由2知,單調(diào)減區(qū)間為 ,并由此得到當(dāng),x=-1時(shí),
,并由此得到當(dāng),x=-1時(shí), ,當(dāng)x=1時(shí),
,當(dāng)x=1時(shí),
解:(1) 是奇函數(shù),
是奇函數(shù), 。
。
即 ,
, ,
, ………………2分
………………2分
 ,又
,又 ,
, ,
, ,
,
(2)任取 ,且
,且 ,
,
 ,………………6分
,………………6分
 ,
,
 ,
, ,
, ,
, ,
,
 在(-1,1)上是增函數(shù)。…………………………………………8分
在(-1,1)上是增函數(shù)。…………………………………………8分
(3)單調(diào)減區(qū)間為 …………………………………………10分
…………………………………………10分
當(dāng),x=-1時(shí), ,當(dāng)x=1時(shí),
,當(dāng)x=1時(shí), 。
。
已知函數(shù) ,其中
,其中 .
.
(1)若 在
在 處取得極值,求曲線
處取得極值,求曲線 在點(diǎn)
在點(diǎn)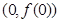 處的切線方程;
處的切線方程;
(2)討論函數(shù) 在
在 的單調(diào)性;
的單調(diào)性;
(3)若函數(shù) 在
在 上的最小值為2,求
上的最小值為2,求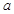 的取值范圍.
的取值范圍.
【解析】第一問, 因
因 在
在 處取得極值
處取得極值
所以, ,解得
,解得 ,此時(shí)
,此時(shí) ,可得求曲線
,可得求曲線 在點(diǎn)
在點(diǎn)
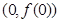 處的切線方程為:
處的切線方程為:
第二問中,易得 的分母大于零,
的分母大于零,
①當(dāng) 時(shí),
時(shí),
 ,函數(shù)
,函數(shù) 在
在 上單調(diào)遞增;
上單調(diào)遞增;
②當(dāng) 時(shí),由
時(shí),由 可得
可得 ,由
,由 解得
解得
第三問,當(dāng) 時(shí)由(2)可知,
時(shí)由(2)可知, 在
在 上處取得最小值
上處取得最小值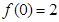 ,
,
當(dāng) 時(shí)由(2)可知
時(shí)由(2)可知 在
在 處取得最小值
處取得最小值 ,不符合題意.
,不符合題意.
綜上,函數(shù) 在
在 上的最小值為2時(shí),求
上的最小值為2時(shí),求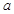 的取值范圍是
的取值范圍是
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com