
題目列表(包括答案和解析)
.若直線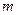 被兩平行線
被兩平行線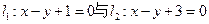 所截得的線段的長為
所截得的線段的長為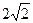 ,則
,則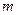 的傾斜
的傾斜 角可以是
角可以是
①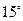 ②
②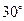 ③
③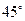 ④
④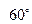 ⑤
⑤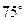
其中正確答案的序號是 .(寫出所有正確答案的序號)
.三、解答題:本大題共6小題,共75分. 解答應寫出文字說明、證明過程或演算步驟.
16. (本題滿分12分)
已知函數 為偶函數, 且
為偶函數, 且
(1)求 的值;
的值;
(2)若 為三角形
為三角形 的一個內角,求滿足
的一個內角,求滿足 的
的 的值.
的值.
.本題有(1)、(2)、(3)三個選答題,每題7分,請考生任選2題作答,滿分14分.如果多做,則按所做的前兩題記分.作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將所選題號填入括號中.
(1)(選修4—2 矩陣與變換)(本小題滿分7分)
已知矩陣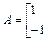
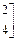 ,向量
,向量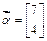 .
.
(Ⅰ) 求矩陣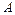 的特征值
的特征值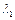 、
、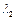 和特征向量
和特征向量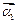 、
、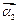 ;
;
(Ⅱ)求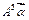 的值.
的值.
(2)(選修4—4 參數方程與極坐標)(本小題滿分7分)
在極坐標系中,過曲線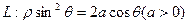 外的一點
外的一點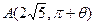 (其中
(其中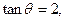
 為銳角)作平行于
為銳角)作平行于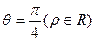 的直線
的直線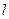 與曲線分別交于
與曲線分別交于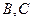 .
.
(Ⅰ) 寫出曲線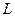 和直線
和直線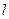 的普通方程(以極點為原點,極軸為
的普通方程(以極點為原點,極軸為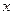 軸的正半軸建系);
軸的正半軸建系);
(Ⅱ)若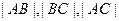 成等比數列,求
成等比數列,求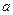 的值.
的值.
(3)(選修4—5 不等式證明選講)(本小題滿分7分)
已知正實數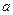 、
、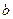 、
、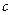 滿足條件
滿足條件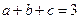 ,
,
(Ⅰ) 求證: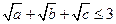 ;
;
(Ⅱ)若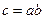 ,求
,求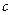 的最大值.
的最大值.
.15. (考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評閱記分.)
A.(不等式選做題)不等式 的解集為 .
的解集為 .
B.(幾何證明選做題)如圖,直線 與圓
與圓 相切于點
相切于點 ,割線
,割線 經過圓心
經過圓心 ,弦
,弦 ⊥
⊥ 于點
于點 ,
,  ,
, ,則
,則 .
.
C.(坐標系與參數方程選做題)在極坐標系中,圓 的圓心到直線
的圓心到直線 的距離為 .
的距離為 .
.(本小題滿分12分)
某單位實行休年假制度三年以來,50名職工休年假的次數進行的調查統計結果如下表所示:
| 休假次數 |  | 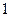 | 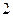 | 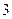 |
| 人數 | 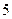 | 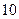 | 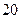 | 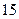 |
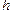 表示這兩人休年假次數之和,記“函數
表示這兩人休年假次數之和,記“函數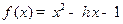 在區間
在區間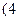 ,
,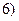 上有且只有一個零點”為事件
上有且只有一個零點”為事件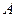 ,求事件
,求事件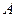 發生的概率
發生的概率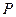 ;
;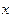 表示這兩人休年假次數之差的絕對值,求隨機變量
表示這兩人休年假次數之差的絕對值,求隨機變量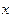 的分布列及數學期望
的分布列及數學期望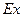 .
.1.B 2.B 3.A 4.C 5.C 6.B 7.D 8.B 9.C 10.B 
11.A 12.D
【解析】
1. ,所以選B.
,所以選B.
2. 的系數是
的系數是 ,所以選B.
,所以選B.
3. ,所以選
,所以選 .
.
4. 為鈍角或
為鈍角或 ,所以選C
,所以選C
5. ,所以選C.
,所以選C.
6. ,所以選B.
,所以選B.
7. ,所以選D.
,所以選D.
8.化為 或
或 ,所以選B.
,所以選B.
9.將 左移
左移 個單位得
個單位得 ,所以選A.
,所以選A.
10.直線 與橢圓
與橢圓 有公共點
有公共點 ,所以選B.
,所以選B.
11.如圖,設 ,則
,則 ,
,

 ,
,
 ,從而
,從而 ,因此
,因此 與底面所成角的正弦值等于
與底面所成角的正弦值等于 .所以選A.
.所以選A.
12.畫可行域 可知符合條件的點 是:
是: 共6個點,故
共6個點,故 ,所以選D.
,所以選D.
二、
13.185. .
.
14.60. .
.
15. ,由
,由 ,得
,得
 .
.
16. .如圖:
.如圖:

如圖,可設 ,又
,又 ,
,
 .
.
當 面積最大時,
面積最大時, .點
.點 到直線
到直線 的距離為
的距離為 .
.
三、
17.(1)由三角函數的定義知: .
.
(2)


 .
.
18.(1)設兩年后出口額恰好達到危機前出口額的事件為 ,則
,則 .
.
(2)設兩年后出口額超過危機前出口額的事件為 ,則
,則 .
.
19.(1)設 與
與 交于點
交于點 .
.



從而 ,即
,即 ,又
,又 ,且
,且
 平面
平面 為正三角形,
為正三角形, 為
為 的中點,
的中點,
 ,且
,且 ,因此,
,因此, 平面
平面 .
.
(2) 平面
平面 ,∴平面
,∴平面 平面
平面 又
又 ,∴平面
,∴平面 平面
平面
設 為
為 的中點,連接
的中點,連接 ,則
,則 ,
,
 平面
平面 ,過點
,過點 作
作 ,連接
,連接 ,則
,則 .
.
 為二面角
為二面角 的平面角.
的平面角.
在 中,
中, .
.
又 .
.
20.(1)


(2)

又


綜上: .
.
21.(1) 的解集為(1,3)
的解集為(1,3)
∴1和3是 的兩根且
的兩根且