精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

A．（不等式選做題）若關于x的不等式|x+3|-|x+2|≥log₂a有解，則實數a的取值范圍是：

 

．
B．（幾何證明選做題）如圖，四邊形ABCD是圓O的內接四邊形，延長AB和DC相交于點P．若

PB

PA

=

1

2

，

PC

PD

=

1

3

，則

BC

AD

的值為

 

．
C．（坐標系與參數方程選做題）設曲線C的參數方程為

x=3+2 2 cosθ y=-1+2 2 sinθ

（θ為參數），以原點為極點，x軸正半軸為極軸建立極坐標系，直線l的極坐標方程為ρ=

2

cosθ-sinθ

，則曲線C上到直線l距離為

2

的點的個數為：

 

．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

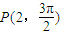A．（坐標系與參數方程選做題）在極坐標系中，點到直線l：3ρcosθ-4ρsinθ=3的距離為    ．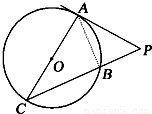 
B．（幾何證明選講選做題）已知PA是圓O的切線，切點為A，PA=2，AC是圓O的直徑，PC與圓O交于點B，PB=1，則圓O的半徑R的長為    ．

查看答案和解析>>

一、

1．D      2．C       3．B       4．D      5．C       6．A      7．D      8．B       9．C       10．C

11．D     12．A

【解析】

5．解：，則．

6．解：線性規劃問題可先作出可行域（略），設，則，可知在點（1，1）處取最小值，．

7．解：，由條件知曲線在點（0，1）處的切線斜率為，則．

8．解：如圖

正四棱錐中，取中點，連接、，易知就是側面與底面所成角，面，則．

9．解：，展開式中含的項是，其系數是．

10．解：，其值域是．

11．解：，設離心率為，則，由知．

12．解：如圖

正四面體中，是中心，連，此四面體內切球與外接球具有共同球心，必在上，并且等于內切球半徑，等于外接球半徑．記面積為，則，從而

．

二、填空題

13．．

解：，與共線．

14．120種．

       解：按要求分類相加，共有種，或使用間接法：種．

15．．

       解：曲線 ①，化作標準形式為，表示橢圓，由于對稱性，取焦點，過且傾角是135°的弦所在直線方程為：，即 ②，聯立式①與式②消去得：

，由弦長公式得：．

16．充要條件①：底面是正三角形，頂點在底面的射影恰是底面的中心．

充要條件②：底面是正三角形，且三條側棱長相等，

再如：底面是正三角形，且三個側面與底面所成角相等；底面是正三角形，且三條側棱與底面所成角相等；三條側棱長相等，且三個側面與底面所成角相等；三個側面與底面所成角相等，三個側面兩兩所成二面角相等．

三、解答題

17．解：設等差數列的公差為、、成等比數列，即，

，得或．

       時是常數列，，前項和

       時，的前項和

       或．

18．解：，則，，．

由正弦定理得：

       ，

       ，則

       ．

19．解：已知甲擊中9環、10環的概率分別是0．3、0．2，則甲擊中8環及其以下環數的概率是0．5；乙擊中9環、10環的概率分別為0．4、0．3，則乙擊中8環及其以下環數的概率是0．3；丙擊中9環、10環的概率是0．6、0．4，0．6+0．4=1，則丙擊中8環及其以下環數是不可能事件．

       （1）記在一輪比賽中“丙擊中的環數不超過甲擊中的環數”為事件，包括“丙擊中9環且甲擊中9或10環”、“丙擊中10環且甲擊中10環”兩個互斥事件，則

       ．

       （2）記在一輪比賽中，“甲擊中的環數超過丙擊中的環數”為事件，“乙擊中的環數超過丙擊中的環數”為事件，則與相互獨立，且，．

       所以在一輪比賽中，甲、乙擊中的環數都沒有超過丙擊中的環數的概率為：

       ．

20．（1）證：已知是正三棱柱，取中點，中點，連，，則、、兩兩垂直，以、、為、、軸建立空間直角坐標系，又已知，

則．

，，則，又因與相交，故面．

（2）解：由（1）知，是面的一個法向量．

，設是面的一個法向量，則①，②，取，聯立式①與式②解得，則．

              二面角是銳二面角，記其大小為．則

              ，

二面角的大小，亦可用傳統方法解決（略）．

21．解：．

       （1）在處取得極值，則．

       （2），

              恒成立，必有解．

              易知函數圖象（拋物線）對稱軸方程是．

              在上是增函數，則時恒有，進而必有（數形結合）

              或或，

              故的取值范圍是：．

22．解：（1）已知，求得線段的兩個三等分點、，直線過時，，直線過時，，故或．

（2）已知是橢圓短軸端點和焦點，易求得橢圓方程是：，所在直線的方程為．

直線與橢圓相交于、，設，，由直線與線段相交（交點不與、重合）知．

點在橢圓上，則，解得到直線的距離

，

點到直線的距離；

設，則，由知，則：

，

當即時，取到最大值．

_www.ks5u.com，0與中，0距更遠，當且時，

，

．

∴四邊形的面積，當時，．