好吊视频一区二区三区四区,国产伦精品一区二区三区视频黑人,国产成一区二区

已知A.B.C的坐標(biāo)分別為A.C().． (1)若.求角的值, (2)若.求的值．【查看更多】

(本大題滿分12分)
已知A、B、C的坐標(biāo)分別為A(3，0)、B(0，3)、C()，．
(1)若，求角的值；
(2)若，求的值．

查看答案和解析>>

(本小題滿分12分)已知A、B、C三個箱子中各裝有2個完全相同的球，每個箱子里的球，有一個球標(biāo)著號碼1，另一個球標(biāo)著號碼2．現(xiàn)從A、B、C三個箱子中各摸出1個球．

(I)若用數(shù)組(x，y，z)中的x、y、z分別表示從A、B、C三個箱子中摸出的球的號碼，請寫出數(shù)組(x，y，z)的所有情形，并回答一共有多少種；

(Ⅱ)如果請您猜測摸出的這三個球的號碼之和，猜中有獎．那么猜什么數(shù)獲獎的可能性

最大?請說明理由． ’

查看答案和解析>>

(本小題滿分12分)

已知A、B、C為的三個內(nèi)角，向量，且

（Ⅰ）求的值；

（Ⅱ）求C的最大值，并判斷此時的形狀.

查看答案和解析>>

(本小題滿分12分)
已知△ABC的三邊長為a、b、c，且其中任意兩邊長均不相等.若成等差數(shù)列.
(1)比較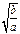與的大小，并證明你的結(jié)論;
(2)求證B不可能是鈍角.

查看答案和解析>>

(本小題滿分12分)

已知在銳角△ABC中，a, b, c分別為角A、B、C所對的邊，向量，，.

(1)求角A的大小；

(2)若a=3，求△ABC面積的最大值.

查看答案和解析>>

一．選擇題：DCBBA DACCA

二．填空題：11．4x－3y－17 = 0　　12．33　　13．
　　　　　　14．　　15．

三．解答題：

16．(1)解：∵，                                  2分
∴由得：，即              4分
又∵，∴                                                                                    6分

(2)解：                                    8分
由得：，即          10分
兩邊平方得：，∴                                          12分

17．方法一

(1)證：∵CD⊥AB，CD⊥BC，∴CD⊥平面ABC 2分
又∵CDÌ平面ACD，∴平面ACD⊥平面ABC　　 4分

(2)解：∵AB⊥BC，AB⊥CD，∴AB⊥平面BCD，故AB⊥BD
∴∠CBD是二面角C－AB－D的平面角 6分
∵在Rt△BCD中，BC = CD，∴∠CBD = 45°
即二面角C－AB－D的大小為45° 8分

(3)解：過點B作BH⊥AC，垂足為H，連結(jié)DH
∵平面ACD⊥平面ABC，∴BH⊥平面ACD，
∴∠BDH為BD與平面ACD所成的角 10分
設(shè)AB = a，在Rt△BHD中，，
∴
又，∴ 12分

方法二
(1)同方法一                                                                                                               4分
(2)解：設(shè)以過B點且∥CD的向量為x軸，為y軸和z軸建立如圖所示的空間直角坐標(biāo)系，設(shè)AB = a，則A(0，0，a)，C(0，1，0)，D(1，1，0)， = (1，1，0)， = (0，0，a)
平面ABC的法向量 = (1，0，0)
設(shè)平面ABD的一個法向量為n = (x，y，z)，則

取n = (1，－1，0)                           6分

∴二面角C－AB－D的大小為45°                                                                           8分

(3)解： = (0，1，－a)， = (1，0，0)， = (1，1，0)
設(shè)平面ACD的一個法向量是m = (x，y，z)，則
∴可取m = (0，a，1)，設(shè)直線BD與平面ACD所成角為，則向量、m的夾角為
故 10分
即
又，∴ 12分

18．解：該商場應(yīng)在箱中至少放入x個其它顏色的球，獲得獎金數(shù)為，
則= 0，100，150，200
，，
， 8分
∴的分布列為

0

100

150

200

P

19．(1)解：設(shè)M (x，y)，在△MAB中，| AB | = 2，
∴
即 2分
因此點M的軌跡是以A、B為焦點的橢圓，a = 2，c = 1
∴曲線C的方程為． 4分

(2)解法一：設(shè)直線PQ方程為 (∈R)
由得：                                                            6分
顯然，方程①的，設(shè)P(x₁，y₁)，Q(x₂，y₂)，則有

                                                           8分
令，則t≥3，                                                             10分
由于函數(shù)在[3，＋∞)上是增函數(shù)，∴
故，即S≤3
∴△APQ的最大值為3                                                                                              12分

解法二：設(shè)P(x₁，y₁)，Q(x₂，y₂)，則
當(dāng)直線PQ的斜率不存在時，易知S = 3
設(shè)直線PQ方程為
由得： ①                                         6分
顯然，方程①的△＞0，則
∴                                    8分
                                10分
　　　　
令，則，即S＜3

∴△APQ的最大值為3 12分

20．(1)解：∵，
∴ 2分
當(dāng)時，
∵當(dāng)時，，此時函數(shù)遞減；
當(dāng)時，，此時函數(shù)遞增；
∴當(dāng)時，F(xiàn)(x)取極小值，其極小值為0． 4分

(2)解：由(1)可知函數(shù)和的圖象在處有公共點，
因此若存在和的隔離直線，則該直線過這個公共點．
設(shè)隔離直線的斜率為k，則直線方程為，即              6分
由，可得當(dāng)時恒成立
由得：                                                                              8分
下面證明當(dāng)時恒成立．
令，
則，                                                                           10分
當(dāng)時，．
∵當(dāng)時，，此時函數(shù)遞增；
當(dāng)時，，此時函數(shù)遞減；
∴當(dāng)時，取極大值，其極大值為0．                                                        12分
從而，即恒成立．
∴函數(shù)和存在唯一的隔離直線．                                              13分

21．(1)解：記
令x = 1得：
令x =－1得：
兩式相減得：
∴ 2分
當(dāng)n≥2時，
當(dāng)n = 1時，，適合上式
∴ 4分

(2)解：
注意到 6分
令，
則
∴
故，即 8分

(3)解：
　　　 (n≥2)                                                                        10分
∴
　        12分
∵
∴                                                       14分

同步練習(xí)冊答案

國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表

湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)

違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
版權(quán)聲明：本站所有文章，圖片來源于網(wǎng)絡(luò)，著作權(quán)及版權(quán)歸原作者所有，轉(zhuǎn)載無意侵犯版權(quán)，如有侵權(quán)，請作者速來函告知，我們將盡快處理，聯(lián)系qq：3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網(wǎng)安備42018502000812號

精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

<ul id="sogya"></ul>

精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

練習(xí)冊

高中

初中

小學(xué)