
題目列表(包括答案和解析)
求由拋物線 與直線
與直線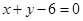 及
及 所圍成圖形的面積.
所圍成圖形的面積.
【解析】首先利用已知函數(shù)和拋物線作圖,然后確定交點坐標,然后利用定積分表示出面積為 ,所以得到
,所以得到 ,由此得到結(jié)論為
,由此得到結(jié)論為
解:設所求圖形面積為 ,則
,則

 =
= .即所求圖形面積為
.即所求圖形面積為 .
.

 (a,b∈Z),曲線y=f(x)在點(2,f(2))處的切線方程為y=3.
(a,b∈Z),曲線y=f(x)在點(2,f(2))處的切線方程為y=3.某化工廠擬建一座平面圖形為矩形且面積為162平方米的三級污水處理池,池的深度一定(平面圖如圖所示).如果池四周圍墻建造單價為400元/米,中間兩道隔墻建造單價為248元/米,池底建造單價為80元/米2,水池所有墻的厚度忽略不計,試設計污水處理池的長和寬,使總造價最低,并求出最低總造價。

【解析】本試題主要考查導數(shù)在研究函數(shù)中的運用。首先設變量
設寬為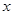 則長為
則長為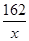 ,依題意,總造價
,依題意,總造價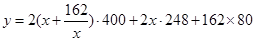
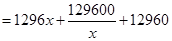
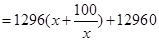
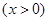
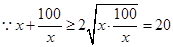 當且僅當
當且僅當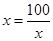 即
即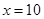 取等號
取等號
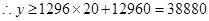 (元)得到結(jié)論。
(元)得到結(jié)論。
設寬為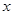 則長為
則長為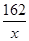 ,依題意,總造價
,依題意,總造價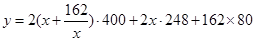
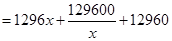
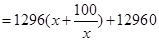
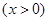 ………6分
………6分
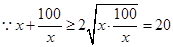 當且僅當
當且僅當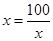 即
即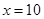 取等號
取等號
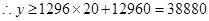 (元)……………………10分
(元)……………………10分
故當處理池寬為10米,長為16.2米時能使總造價最低,且最低總造價為38880元
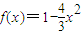 的一部分,欄柵與矩形區(qū)域的邊界交于點M,N,交曲線于點P,則△OMN(O為坐標原點)的面積的最小值為 .
的一部分,欄柵與矩形區(qū)域的邊界交于點M,N,交曲線于點P,則△OMN(O為坐標原點)的面積的最小值為 .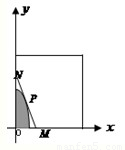
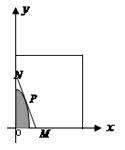 某建筑公司要在一塊寬大的矩形地面(如圖所示)上進行開發(fā)建設,陰影部分為一公共設施建設不能開發(fā),且要求用欄柵隔開(欄柵要求在一直線上),公共設施邊界為曲線
某建筑公司要在一塊寬大的矩形地面(如圖所示)上進行開發(fā)建設,陰影部分為一公共設施建設不能開發(fā),且要求用欄柵隔開(欄柵要求在一直線上),公共設施邊界為曲線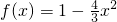 的一部分,欄柵與矩形區(qū)域的邊界交于點M,N,交曲線于點P,則△OMN(O為坐標原點)的面積的最小值為________.
的一部分,欄柵與矩形區(qū)域的邊界交于點M,N,交曲線于點P,則△OMN(O為坐標原點)的面積的最小值為________.國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com