
�}Ŀ�б�(�����𰸺ͽ���)
��֪�c(di��n) ��A
��A �ϵĄ�(d��ng)�c(di��n)����
�ϵĄ�(d��ng)�c(di��n)���� ����
���� �S�ϣ�
�S�ϣ� �S�������
�S������� ����(xi��n)��
����(xi��n)�� ���c(di��n)
���c(di��n) ��܉�E������(xi��n)
��܉�E������(xi��n) ���^(gu��)���c(di��n)
���^(gu��)���c(di��n)
 ����һ�l�c
����һ�l�c �S����ֱ��ֱ��(xi��n)
�S����ֱ��ֱ��(xi��n) �����c����(xi��n)
�����c����(xi��n) ����
���� ��
�� ���c(di��n)��
���c(di��n)��
��I��������(xi��n) �ķ��̣�
�ķ��̣�
��II��ԇ�C������ �S�ϴ��ڶ��c(di��n)
�S�ϴ��ڶ��c(di��n) ��ʹ��
��ʹ�� ���ܱ�
���ܱ� �Sƽ��
�Sƽ��
����������һ��(w��n)���O(sh��) ������(xi��n)
������(xi��n) �ϵ�����һ�c(di��n)���t�c(di��n)
�ϵ�����һ�c(di��n)���t�c(di��n) �ڈA
�ڈA �ϣ�
�ϣ�
�� ������(xi��n)
������(xi��n) �ķ��̞�
�ķ��̞�
�ڶ���(w��n)�У��O(sh��)�c(di��n) ������(bi��o)��
������(bi��o)�� ��ֱ��(xi��n)
��ֱ��(xi��n) �ķ��̞�
�ķ��̞� ������������������3�֡� ��
������������������3�֡� ��
��������(xi��n) �ķ���
�ķ��� ���ɵá�
���ɵá�
�� ����
����
�_���Y(ji��)Փֱ��(xi��n) �c����(xi��n)
�c����(xi��n) ���Ѓɂ�(g��)�����c(di��n)��
���Ѓɂ�(g��)�����c(di��n)��
Ȼ���O(sh��)�c(di��n) ,
, ������(bi��o)�քe
������(bi��o)�քe ,
,  ���t
���t ��
��
Ҫʹ ��
�� �Sƽ�֣�ֻҪ
�Sƽ�֣�ֻҪ �õ���
�õ���
��1���O(sh��) ������(xi��n)
������(xi��n) �ϵ�����һ�c(di��n)���t�c(di��n)
�ϵ�����һ�c(di��n)���t�c(di��n) �ڈA
�ڈA �ϣ�
�ϣ�
�� ������(xi��n)
������(xi��n) �ķ��̞�
�ķ��̞� �� ������������2��
�� ������������2��
��2���O(sh��)�c(di��n) ������(bi��o)��
������(bi��o)�� ��ֱ��(xi��n)
��ֱ��(xi��n) �ķ��̞�
�ķ��̞� ������������������3�֡� ��
������������������3�֡� ��
��������(xi��n) �ķ���
�ķ��� ���ɵá�
���ɵá� ������5��
������5��
�� ����
���� ��
��
��ֱ��(xi��n) �c����(xi��n)
�c����(xi��n) ���Ѓɂ�(g��)�����c(di��n)����Ҳ�ɸ���(j��)�c(di��n)M�ڙE�A
���Ѓɂ�(g��)�����c(di��n)����Ҳ�ɸ���(j��)�c(di��n)M�ڙE�A �ă�(n��i)���õ��˽Y(ji��)Փ��
�ă�(n��i)���õ��˽Y(ji��)Փ��
������������6��
�O(sh��)�c(di��n) ,
, ������(bi��o)�քe
������(bi��o)�քe ,
,  ���t
���t ��
��
Ҫʹ ��
�� �Sƽ�֣�ֻҪ
�Sƽ�֣�ֻҪ ��
������������9��
��
������������9��
�� ��
�� �� ������������10��
�� ������������10��
Ҳ���� ��
�� ��
��
�� ����ֻҪ
����ֻҪ �� ������������12�֡�
�� ������������12�֡�
��(d��ng) �r(sh��)����������(du��)�����s���������Ķ�
�r(sh��)����������(du��)�����s���������Ķ� ���ܱ�
���ܱ� �Sƽ�֣�
�Sƽ�֣�
������x�S�ϴ��ڶ��c(di��n) ��ʹ��
��ʹ�� ���ܱ�
���ܱ� �Sƽ��
�Sƽ��
��֪������ԭ�c(di��n)�����c(di��n)�� �S�ϵęE�A
�S�ϵęE�A ���x���ʞ�
���x���ʞ� ���ҽ�(j��ng)�^(gu��)�c(di��n)
���ҽ�(j��ng)�^(gu��)�c(di��n)
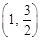 .
.
������E�A �ķ��̣�
�ķ��̣�
�����Ƿ���^(gu��)�c(di��n) ��2,1����ֱ��(xi��n)
��2,1����ֱ��(xi��n) �c�E�A
�c�E�A �ཻ�ڲ�ͬ�ă��c(di��n)
�ཻ�ڲ�ͬ�ă��c(di��n) ���M(m��n)��
���M(m��n)�� �������ڣ����ֱ��(xi��n)
�������ڣ����ֱ��(xi��n) �ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
����������һ��(w��n)�����O(sh��)�E�A �ķ��̞�
�ķ��̞� �����}���
�����}���
���
�ڶ���(w��n)������ֱ��(xi��n) �M(m��n)��l���ķ��̞�
�M(m��n)��l���ķ��̞� ������E�A
������E�A �ķ��̵�
�ķ��̵�
 ��
��
��?y��n)�ֱ��(xi��n) �c�E�A
�c�E�A �ཻ�ڲ�ͬ�ă��c(di��n)
�ཻ�ڲ�ͬ�ă��c(di��n) ���O(sh��)
���O(sh��) ���c(di��n)������(bi��o)�քe��
���c(di��n)������(bi��o)�քe�� ��
��
����
���� ����á�
����á�
�⣺���O(sh��)�E�A �ķ��̞�
�ķ��̞� �����}���
�����}���
��� ���ʙE�A
���ʙE�A �ķ��̞�
�ķ��̞� ������������������4��
������������������4��
��������ֱ��(xi��n) �M(m��n)��l���ķ��̞�
�M(m��n)��l���ķ��̞� ������E�A
������E�A �ķ��̵�
�ķ��̵�
 ��
��
��?y��n)�ֱ��(xi��n) �c�E�A
�c�E�A �ཻ�ڲ�ͬ�ă��c(di��n)
�ཻ�ڲ�ͬ�ă��c(di��n) ���O(sh��)
���O(sh��) ���c(di��n)������(bi��o)�քe��
���c(di��n)������(bi��o)�քe�� ��
��
����
���� ��
��
�� ��
��
��?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912284792138316/SYS201207091229220620471975_ST.files/image009.png">���� ��
��
����
 ��
��
�� ��
��
���� �����
����� ��
��
��?y��n)�A,B�鲻ͬ�ă��c(di��n)������k=1/2��
���Ǵ���ֱ��(xi��n)L1�M(m��n)��l�����䷽�̞�y=1/2x
����С�}�M(m��n)��16�֣�
��ֱ������(bi��o)ϵ �У�ֱ��(xi��n)
�У�ֱ��(xi��n) �c
�c �S�����S��
�S�����S�� �S�����S�քe�ཻ��
�S�����S�քe�ཻ�� ���c(di��n)
���c(di��n)
 �ă�(n��i)�ЈA���
�ă�(n��i)�ЈA���
��1������� �İ돽��1��
�İ돽��1�� �c��
�c�� �����c(di��n)
�����c(di��n) ����ֱ��(xi��n)
����ֱ��(xi��n) �ķ���
�ķ���
��2������� �İ돽��1���C����(d��ng)
�İ돽��1���C����(d��ng) ����e�����L(zh��ng)��С�r(sh��)���˕r(sh��)��
����e�����L(zh��ng)��С�r(sh��)���˕r(sh��)�� ��ͬһ������
��ͬһ������
��3����� �ķ��̞�
�ķ��̞�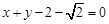 ��
�� ���
��� ����һ�c(di��n)����
����һ�c(di��n)���� ����ֵ
����ֵ
����С�}�M(m��n)��16�֣�
��ֱ������(bi��o)ϵxOy�У�ֱ��(xi��n)l�cx�S�����S��y�S�����S�քe�ཻ��A��B���c(di��n)����AOB�ă�(n��i)�ЈA��AM��
��1������AM�İ돽��1��l�c�AM�����c(di��n)C ( ��1��
��1�� )����ֱ��(xi��n)l�ķ��̣�
)����ֱ��(xi��n)l�ķ��̣�
��2������AM�İ돽��1���C������(d��ng)��AOB����e�����L(zh��ng)��С�r(sh��)���˕r(sh��)��AOB��ͬһ��(g��)�����Σ�
��3�����l�ķ��̞�x��y��2�� ��0��P��AM����һ�c(di��n)����
��0��P��AM����һ�c(di��n)���� ��
�� ��
�� ����ֵ��
����ֵ��
����С�}�M(m��n)��16�֣�
��ֱ������(bi��o)ϵxOy�У�ֱ��(xi��n)l�cx�S�����S��y�S�����S�քe�ཻ��A��B���c(di��n)����AOB�ă�(n��i)�ЈA��AM��
��1������AM�İ돽��1��l�c�AM�����c(di��n)C (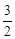 ��1��
��1��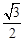 )����ֱ��(xi��n)l�ķ��̣�
)����ֱ��(xi��n)l�ķ��̣�
��2������AM�İ돽��1���C������(d��ng)��AOB����e�����L(zh��ng)��С�r(sh��)���˕r(sh��)��AOB��ͬһ��(g��)�����Σ�
��3�����l�ķ��̞�x��y��2��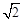 ��0��P��AM����һ�c(di��n)����
��0��P��AM����һ�c(di��n)���� ��
��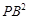 ��
��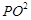 ����ֵ��
����ֵ��
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com